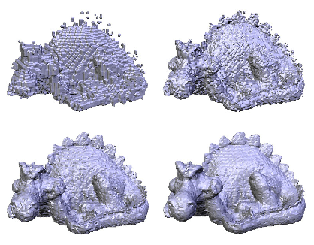
Multiresolution Modeling Using Fractal Image Compression Techniques
Óscar Belmonte, Sergio Sancho and José Ribelles
EG UK Theory and Practice of Computer Graphics (2010)
This work presents a new approach to the multiresolution modeling of polygonal meshes. This approach is based on the theoretically well-established fractal image compression techniques. A polygonal mesh is represented as a fractal using an iterated function system (IFS). In this way, a level of detail can be obtained over a region of the mesh by successively iterating the IFS. The main advantage is that it becomes possible to recover new levels of detail that were not present in the original mesh, so that the quality is not lost as the observer approaches the mesh. Another characteristic is that the same representation can be used over textures, and in this case the algorithm is directly implemented over the GPU. T he visualization time obtained allows this new approach to be used in real-time interactive computer graphic applications.
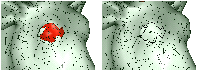
An Improved Discrete Level of Detail Model Through an Incremental Representation
J. Ribelles, A. López and O. Belmonte
EG UK Theory and Practice of Computer Graphics (2010)
Real-time applications such as computer and video games, virtual reality and scientific simulation require render- ing of complex models for realism. Graphics rendering engines include multiresolution modelling techniques to accelerate the visualization process. The Discrete Level of Detail framework (DLoD) is usually the most popular while the Continuous Level of Detail framework (CLoD) is still not as widely used by software developers. In this paper, we first discuss the benefits and drawbacks of both frameworks. Then, we present a model based on coding a discrete number of levels of detail (LoDs), with more LoDs coded than is usual in DLoD, and with an incremental representation, which is often used in CLoD. This model obtains a performance similar to DLoD by providing optimized LoDs for efficient visualization, while the popping effect is imperceptible. We present specific proposals for each of the three main stages involved in multiresolution processing: geometry simplification, construction of the incremental representation and retrieval of either uniform or view-dependent LoDs.
Acceleration techniques applied to non-photorealistic visualisation of polygonal models
O. Belmonte, J. Dingliana
Proceedings of the Eurographics Irish Chapter Workshop 2007, pp: 81-87,
Dublin, Ireland, December 2007
The aim of this work is to develop acceleration techniques for the non-photorealistic rendering of polygonal models based on lines. The first group of techniques presented is based on using differential geometry to reduce the number of triangles that need to be checked in order to determine the set of suitable lines; The second group is based on the use of multiresolution modelling and, more particularly the development of a simplification algorithm that preserves those regions on the polygonal mesh with sharp changes in their curvature. The final result is a reduction in the number of triangles that are checked in order to determine the lines needed in a nonphotorealistic line-based rendering and, consequently, an increase in the number of frames per second that can be rendered.
Triangle Strip Mutiresolution Modelling Using Sorted Edges
O. Belmonte, S. Aguado, S. Sancho
Lecture Notes in Computer Science 3992. Fifth International Workshop on
Computer Graphics and Geometric Modeling (CGGM 2006). pp: 350-357. 2006.
This paper presents a new multiresolution model based exclusively on the triangle strip primitive. The model is independent of the initial set of triangle strips and the simplification method used to obtain the lower resolution versions of the original model. The information stored in the data structures is sorted to minimise the time needed to recover a Level of Detail (LoD). The orientation of triangles in each strip is maintained as the model is simplified, so back-face culling can be used. The main result is a dramatic improvement in the rendering time.
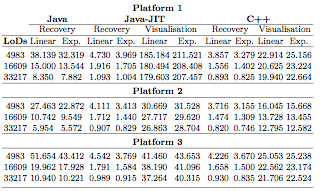
Performance of Java versus C++ in a Real-Time Computer Graphics Application
O. Belmonte, S. Sancho
ICCSA 2006
Computer Graphics applications, and especially Real-Time Computer Graphics, are mostly developed in the C/C++ programming languages. On the other hand, the Java programming language is mature enough to be used in time consuming applications. This work compares the Java programming language versus C/C++ in Real-Time Computer Graphics applications, taking a multiresolution model as a basis for this comparison. The main conclusions are that the Java performance for data recovery is near to C++ but there are a big gap between the visualisation performance in both computer languages.
An approach to improve strip-based multiresolution schemes
F. Ramos, M. Chover, Ó. Belmonte, C. Rebollo,
Journal of WSCG, University of West Bohemia, ISBN/ISSN 1213-6972, Plzen (Czech Republic), vol. 12, num. 1,
pp. 349-354, February, 2004, Václav Skala
Triangles strips have been used extensively for static mesh representation since they are optimised for rendering. This primitive reduces the number of vertices sent to the graphics pipeline and the storage cost. We present an approach to improve multiresolution models that takes into account this connectivity property. Our model uses strips both in data structure and in the render stage, and it offers the following features: easy to be implemented, small storage cost, efficiency and speed.
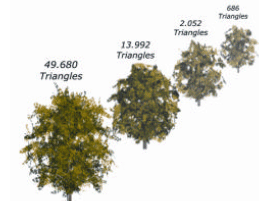
View-Dependent Multiresolution Model for Foliage
Remolar, M. Chover, J. Ribelles, O. Belmonte,
Journal of WSCG, vol. 11(2), 370-378, 2003. ISSN 1213-6972
Real-time rendering of vegetation is one of the most important challenges in outdoor scenes. This is due to the vast amount of polygons that are used to model vegetable species.
Multiresolution modeling has been successfully presented as a solution to the problem of efficient manipulation of highly detailed polygonal surfaces. In order to construct a multiresolution model, a simplification method must be used. The previously introduced Foliage Simplification Algorithm, FSA, obtains different approximations of a tree model. This automatic simplification method diminishes the number of polygons that form the crown while maintaining its leafy appearance.
In this paper a multiresolution model for trees based on this simplification algorithm is presented. Its distinctive property is that the unit of information managed by this scheme is the leaf, four vertices determining two triangles. This characteristic allows us an efficient manipulation of the results obtained by FSA. Our multiresolution representation provides a wide, virtually continuous, range of different approximations that represent the original tree. The main property of this scheme is that trees can be represented with variable resolution: some regions in more detail while the rest is represented in less detail. Here we present the data structures and the traversing algorithms, which favor the extraction of an appropriate level of detail for rendering.

Geometric Simplification of Foliage
I. Remolar, M. Chover, O. Belmonte, J. Ribelles, C. Rebollo,
EUROGRAPHICS'02 Short Presentations, 397-404, Saarbrücken (Germany), September, 2002. ISSN 1017-4565
One of the most important challenges in real-time rendering of outdoor scenes is the representation of vegetation. This is due to the vast amount of polygons that are used to model vegetable species. The present automatic simplification algorithms produce acceptable results in the trunks and the branches, but not in the foliage of a tree. After simplification with the existing methods, the trees seem to be less leafy. In this paper, a new automatic simplification algorithm for this part of the tree is presented, the Foliage Simplification Algorithm. It diminishes the number of polygons in the crown, while maintaining the appearance. It uses a new method, leaf collapse: two leaves disappear to create a new one. The leaves obtained after collapsing preserve an area similar to that of the collapsed leaves.

Efficient Implementation of Multiresolution Triangle Strips
O. Belmonte, I. Remolar, J. Ribelles, M. Chover, M. Fernández. ,
Lecture Notes in Computer Science 2330. Proc. of the Computational
Science 2002 Conference (ICCS 2002). Workshop on Computer Graphics
and Geometric Modeling, Vol. 2, 111-120, Amsterdam (The Netherlands),
April, 2002. ISBN 3-540-43593-X
Triangle meshes are currently the most popular standard model to represent polygonal surfaces. Drawing these meshes as a set of independent triangles involves sending a vast amount of information to the graphic engine. It has been shown that using drawing primitives, such as triangle fans or strips, dramatically reduces the amount of information.
Multiresolution Triangle Strips (MTS) uses the connectivity information to represent a mesh as a set of multiresolution triangles strips. These strips are the basis of both the storage and rendering stages. They allow the efficient management of a wide range of levels of detail. In this paper, we have taken advantage of the coherence property between two levels of detail to decrease the visualisation time. MTS has been compared against Progressive Meshes and Multiresolution Ordered Meshes with Fans, the only model that uses the triangle fan as an alternative to the triangle primitive. In all cases, Multiresolution Triangle Strips obtains a better frame rate.

Multiresolution Modelling Using Connectivity Information
Belmonte, I. Remolar, J. Ribelles, M. Chover, C. Rebollo, M. Fernández,
Journal of WSCG, vol. 10(1), 71-78, 2002. ISSN 1213-6972
Triangle meshes are the most popular standard model to represent polygonal surfaces in Computer Graphics. Drawing these meshes as a set of independent triangles involves sending a vast amount of information sent to the graphic engine. The use of primitives such as fan and strip of triangles, which make use of the connectivity information between the triangles in the mesh, reduces dramatically the amount of information sent to the graphic engine. The Multiresolution Tirangle Strips scheme takes adventage of this characteristic in order to represent a multiresolution model as a set of multiresolution trriangle strips. A multiresolution triangle strip is made of the original strips and all of its Levels of Detail. Each of this multiresolution strips is represented as a graph that is traversed to recover the demanded LoD. A Multiresolution Triangle Strip model uses the triangle strip primitive both in the data structure as in the rendering stage. The Multiresolution Tirangle Strip is compared against the Progressive Meshes multiresolution model, one of the best multiresolution models probably known. The performance of the MTS models in visualising improves drastically PM models.

Multiresolution Triangle Strips,
O. Belmonte, I. Remolar, J. Ribelles, M. Chover, M. Fernández, C. Rebollo,
Proc. of Visualization, Imaging and Image Processing (VIIP 2001), 182-187, Marbella (Spain), September, 2001. ISBN 0-88986-309-1
Most of the previous multiresolution models use exclusively the triangle graphic primitive both in the data structure and in the rendering stage. Only a few models use another graphic primitive in this rendering process and just one uses the triangle fan as the basic primitive of the model. In this paper we present the first multiresolution model, Multiresolution Triangle Strips, that uses the triangle strip in the data structure and in the rendering stage. Each triangle strip is represented as a graph and all levels-of-detail of this strip are stored in it. The extraction algorithm traverses the graph to obtain the triangle strip at the demanded resolution. The use of this primitive speeds up the rendering process as the number of vertices sent to the graphic system is reduced.
Searching Triangle Strips Guided by Simplification Criterion,
O. Belmonte, J. Ribelles, I. Remolar, M. Chover,
Short communications and Posters of 9-th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG 2001), 68-75, Plzen (Czech Republic), February, 2001. ISBN 80-7082-713-0
Triangle strips are widely used as a method to accelerate the visualisation process of polygon models in interactive graphics applications. Another widely used method to improve drawing speed is the utilisation of multiresolution models. These models are constructed based on simplification algorithms. None of the current algorithms for searching strips contemplates the posterior simplification of the initial model. In this paper an algorithm for searching strips is presented. The triangles forming a strip are selected based on a simplification criterion according to the average quadratic error associated with the contraction of edges so that the model is simplified. In this manner the strips encountered are conserved as the model is being simplified. The strips generated in this way may be used to draw the polygon model in an incremental form or to transmit it progressively within a computer network.

Variable Resolution Level-of-detail of Multiresolution Ordered Meshes.
J. Ribelles, A. López, O. Belmonte, I. Remolar, M. Chover,
Proc. of 9-th International Conference in Central Europe on Computer Graphics,
Visualization and Computer Vision (WSCG 2001), Vol. 2, 299-306, Plzen (Czech Republic),
February, 2001. ISBN 80-7082-712-4
Variable resolution level-of-detail is an important application of multiresolution modeling, since te use of different resolutions across the surface allows interactive visualization of highly detailed objects. Multiresolution Ordered Meshes (MOM) was first introduced as a model that achieves the efficient management of an ample range of uniform resolution levels-of-detail and presents reduced storage space requirements. In this paper, we introduce an algorithm capable of retrieving variable resolution levels-of-detail from a multiresolution MOM representation without having to reorganize data in new structures or store new information. The proposed algorithm starts from the level of highest detail and simplifies it adaptively to reach the required resolution in each area of the surface. Experiments with data sets of varying complexity demonstrate that the new algorithm obtains variable resolution levels of detail while retaining the advantages of MOM.

Multiresolution Modelling of Polygonal Surface Meshes Using Triangle Fans.
J. Ribelles, A. López, I. Remolar, O. Belmonte, M. Chover,
Lecture Notes in Computer Science 1953. Proc.of 9th Discrete Geometry for Computer Imagery Conference (DGCI 2000),
431-442, Uppsala (Sweden), December, 2000. ISBN 3-540-41396-0
Multiresolution modelling of polygonal surface meshes has been presented as a solution for the interactive visualisation of scenes formed by hundreds of thousands of polygons. On the other hand, it has been shown that representing surfaces using sets of triangle strips or fans greatly reduces visualisation time and provides an important memory savings. In this paper we present a new method to model polygonal surface meshes. Like the previously explained Multiresolution Ordered Meshes (MOM), this method permits the efficient management of an ample range of approximations of the given model. Furthermore, this method utilises the triangle fan as its basic representation primitive. Experiments realised with data sets of varying complexity demonstrate reduced storage space requirements, while retaining the advantages of MOMs.




