Algoritmos y Estructuras de Datos (VJ1215)

Estas animaciones de David Galles te pueden ayudar a entender las operaciones con árboles binarios de búsqueda y árboles AVL:

• Binary Search Tree

• AVL Tree

Alternativamente, en esta carpeta puedes encontrar una animación realizada por Arsen Gogeshvili, que muestra más detalladamente lo que sucede en las rotaciones dobles. Se puede ejecutar utilizando, por ejemplo, este emulador de Flash, como se indica en el fichero LEEME.

1. Clase de teoría TE1 03-10/10
   Clase de prácticas LA2 y LA4 08/10, LA1 y LA3 10/10

   Los ficheros que puedes encontrar en esta carpeta Conjunto/VersionInicial contienen una implementación del TAD Conjunto en la que se emplea un árbol binario de búsqueda para representar internamente los datos.

   Estudia esa implementación de la clase Conjunto, con ayuda de las explicaciones que se darán en clase y de cualquier otro recurso que consideres adecuado. Puedes consultar al profesor las dudas que tengas.

   Ayuda con C++: punteros por referencia

   Como ayuda para entender para qué sirve pasar punteros por referencia, prueba y entiende lo que sucede en este ejemplo.

   Después realiza este ejercicio.

   En el tema 2 se proporcionó también un primer ejemplo de puntero pasado por referencia, en la primera solución recursiva del ejercicio 4 del tema 2.

2. Clase de prácticas LA2 y LA4 08/10, LA1 y LA3 10/10

   El tiempo estimado de resolución de este ejercicio completo es de 6 horas. Puedes empezar a resolverlo en la primera sesión de prácticas del tema 3, o adelantarte en casa.

   En este ejercicio, parte de la versión inicial de la clase Conjunto, explicada en clase de teoría (ejercicio 1). Si quieres trabajar con OnlineGDB, puedes partir de este enlace y pulsar el botón "Fork this" para obtener una copia editable en la que puedes escribir tus soluciones.

   Compila y prueba tu solución de cada apartado (con tu propio programa de test) antes de pasar al siguiente apartado, asegurándote de que tratas bien todos los casos.

   Ayuda con C++: return y recursión

   En estos ejemplos de errores de programación básica se ilustran errores relacionados con el uso de return que ya no deberías cometer. Fíjate bien en eso por si te sucede y pregunta al profesor en caso de duda.

   1. Añade a la clase Conjunto un método público que devuelva la suma de todos los elementos del conjunto:

      int sumar() const;
      		  

      Resuelve el problema recursivamente, suponiendo que no puedes añadir nada para tener la suma precalculada. Para ello piensa, si pudieses calcular la suma de cada uno de los dos subárboles del árbol, cómo podrías utilizar eso para calcular la suma del árbol.

      Analiza el coste temporal de tu solución.

      Solución

   2. Añade a la clase Conjunto un método público que sume 1 a cada uno de los elementos del conjunto:

      void incrementarTodos();
      		  

      Resuelve el problema recursivamente.

      Analiza el coste temporal de tu solución.

      Solución

   3. Añade un método público que devuelva la talla del conjunto, es decir, la cantidad de datos que contiene.

      int talla() const;
      		  

      Su coste temporal debe ser O(1). Para conseguirlo, puedes añadir atributos y modificar otros métodos.

      Ten en cuenta que la talla del conjunto no cambia si se intenta insertar un elemento que ya estaba o se intenta eliminar un elemento que no estaba.

      No confundas "talla" del conjunto con "altura" del árbol.

      Solución

   4. La versión inicial incluye un método para buscar un dato en el conjunto:

      bool buscar(int) const;
      		  

      Sustituye la implementación no recursiva por una implementación recursiva que tenga el mismo coste temporal.

      Solución

      Aprende más ayudando a otros estudiantes

   5. La versión inicial incluye un método para insertar un dato en el conjunto:

      void insertar(int);
      		  

      Sustituye la implementación recursiva por una implementación no recursiva que tenga el mismo coste temporal.

      Solución (con ejemplos de errores)

   6. Añade un método público que muestre en la salida estándar los elementos del conjunto ordenados de menor a mayor.

      void mostrarOrdenados() const;
      		  

      Su coste temporal debe ser O(n), siendo n la talla del conjunto.

      Ayuda

      Solución (con ejemplos de errores)

   7. Añade un método público que devuelva un vector con los elementos del conjunto ordenados de menor a mayor.

      vector<int> obtenerOrdenados() const;
      		  

      Su coste temporal debe ser O(n), siendo n la talla del conjunto. Analiza su coste espacial.

      Ayuda

      Solución

      Aprende más ayudando a otros estudiantes

      Solución en OnlineGDB

      Ayuda con C++: bucles foreach

      En el enlace anterior se hace uso de un nuevo tipo de bucles introducidos en C++11, que se corresponden con lo que en otros lenguajes se denomina bucles foreach. Para saber más sobre ese tipo de bucles, mira y prueba este ejemplo de uso de los bucles foreach en C++. Hasta ahora no los hemos usado, con el objetivo de ir introduciendo conceptos de C++ gradualmente. Contaremos con ellos a partir de ahora.

   8. [Fuente: ejercicio 4.32 del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss]

      Diseña un algoritmo eficiente para, dado un árbol binario en el que cada nodo contiene un dato de tipo entero, averiguar si es un árbol binario de búsqueda (es decir, para todo nodo, los datos en su suárbol izquierdo son menores o iguales y los datos en su subárbol derecho son mayores o iguales que el dato en el propio nodo).

      Impleméntalo añadiendo el siguiente método privado a la clase Conjunto:

      bool esArbolBinarioDeBusqueda() const;
      		  

      Analiza el coste temporal de tu solución.

      Ayuda

      Solución

      Aprende más ayudando a otros estudiantes

      Prueba de la solución

      En los ficheros anteriores, observa cómo se utiliza el nuevo método privado en los métodos insertar y eliminar para encontrar posibles errores en dichos métodos. Puedes hacer eso mismo, por ejemplo, para comprobar que el resultado de cada inserción utilizando tu solución del apartado siguiente es un arbol binario de búsqueda.

   9. Añade un método público que elimine todos los elementos del conjunto y libere toda la memoria reservada para almacenarlos.

      void vaciar();
      		  

      Debe tener coste temporal O(n), siendo n la talla del conjunto, y debe dejar el conjunto en un estado que permita realizar nuevas operaciones con él, como si estuviese recién construido.

      Solución

      Aprende más ayudando a otros estudiantes

   10. Como solución del ejercicio anterior, un estudiante propone implementar así el método vaciar:

       void Conjunto::vaciar() {
          while (raiz != nullptr)
             eliminar(raiz->dato);
       }
       		  

       Otro estudiante propone la siguiente solución:

       void Conjunto::vaciar() {
          while (raiz != nullptr)
             eliminar(minimoEnSubarbol(raiz));
       }
       		  

       ¿Esas soluciones resuelven correctamente el problema? ¿Cuál es su coste temporal en el peor caso? ¿En qué consiste el peor caso para cada solución? ¿Son mejores estas soluciones propuestas en el ejercicio anterior?

       Solución

   11. Suponiendo que no puedes añadir nada para tener el mínimo precalculado, y aprovechando que ya está implementado el método privado recursivo minimoEnSubarbol en la versión inicial, utilízalo para añadir un método público que devuelva el valor mínimo del conjunto. Debes lanzar una excepción si el conjunto está vacío.

       int consultarMinimo() const;
       		  

       Analiza el coste temporal de esta propuesta.

       En este apartado no nos preocupa la eficiencia del método: mejoraremos eso en el apartado 2.m.

       Solución

   12. Sustituye la implementación recursiva del método privado minimoEnSubarbol por una implementación no recursiva que tenga el mismo coste temporal. Tu solución del apartado anterior debe seguir funcionando.

       Solución

       Aprende más ayudando a otros estudiantes

   13. Sustituye la implementación del método público consultarMinimo por una que tenga coste temporal O(1). Puedes hacer para ello los cambios que consideres conveniente en el resto de la clase (puedes, por tanto, añadir atributos y/o modificar métodos) siempre que con ello no empeore el coste temporal de ningún otro método.

       Solución

3. Partiendo de la implementación del ejercicio anterior (no partiendo de cero) y realizando las modificaciones que consideres conveniente, obtén una implementación del TAD Diccionario que permita almacenar datos de tipo entero (por ejemplo, la puntuación de un jugador) con claves de tipo cadena (por ejemplo, el nombre que identifica al jugador) empleando internamente un árbol binario de búsqueda.

   Puedes utilizar la clase string, que permite comparar cadenas con los operadores relacionales.

   Tu clase Diccionario debe ofrecer los siguientes métodos públicos:

   Diccionario();
   void  insertar(const string &, int); // Recibe clave y dato
   void  eliminar(const string &);      // Recibe clave
   int & buscar(const string &) const;  // Recibe clave, devuelve dato
   void  mostrarOrdenados() const;
   int   talla() const;
   void  vaciar();
   	      

   Observa que son análogos a los del TAD Conjunto, pero ahora las operaciones de eliminación y búsqueda se hacen por clave. La búsqueda devuelve el dato asociado a la clave, por referencia para poderlo modificar, y lanza una excepción en caso de no encontrarlo.

   Los argumentos de tipo cadena los pasamos por referencia constante por el mismo motivo por el que en ejercicios previos hemos pasado vectores por referencia constante: para que no se pierda tiempo creando una copia cada vez que se realiza una llamada. Pasar una cadena por valor tendría coste temporal y espacial O(n), siendo n la longitud de la cadena.

   Este ejemplo de uso podría producir esta salida. Al utilizar claves de tipo string, los elementos del diccionario se muestran ordenados en orden lexicográfico.

   Ayuda con C++: devolución por referencia

   En este ejercicio se pide que el método buscar devuelva el resultado por referencia. Gracias a eso, podremos utilizarlo para hacer, por ejemplo, esto: puntuaciones.buscar("Sevilla") = 66 (lo puedes encontrar en el ejemplo de uso que se ha proporcionado antes).

   Modificar así el dato guardado en un nodo no hace que el árbol interno deje de ser un árbol binario de búsqueda (si existiese ese riesgo, no deberíamos permitirlo). Internamente, los valores que deben cumplir la propiedad de orden de los árboles binarios de búsqueda son las claves, no los datos asociados a las mismas.

   Prueba de la solución

4. 1. Añade a la clase Conjunto un método público que devuelva la altura del árbol:

      int altura() const;
      		  

      Seguimos el convenio de que un árbol formado por un solo nodo tiene altura 0. Si el árbol está vacío, devuelve -1.

      Resuelve el problema recursivamente, suponiendo que no puedes añadir nada para tener la altura precalculada.

      Analiza el coste temporal de tu solución.

      Solución

   2. Si un árbol binario de búsqueda tiene n nodos, ¿entre qué valores mínimo y máximo se encuentra su altura?

      Solución

5. Diseña un algoritmo recursivo cuya entrada sea un árbol binario y cuya salida sea un booleano que indique si todos los nodos tienen cero o dos hijos. ¿Cuál es el coste temporal de tu solución?

   Impleméntalo añadiendo el siguiente método público a la clase Conjunto:

   bool noHayHijoSinHermano() const;
   	      

   Solución

   Prueba de la solución

6. Diseña un algoritmo recursivo cuya entrada sean dos árboles binarios y cuya salida sea un booleano que indique si son iguales (con los mismos datos y la misma estructura). ¿Cuál es el coste temporal de tu solución?

   Impleméntalo añadiendo el siguiente método público a la clase Conjunto:

   bool arbolesIguales(const Conjunto &) const;
   	      

   Solución

   Prueba de la solución

7. Clase de teoría TE1 24/10

   [Fuente: ejercicio 4.40 del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss]

   Este es un ejercicio difícil si es la primera vez que te enfrentas a él. Si no consigues resolverlo, asegúrate de que entiendes la solución para saber aplicarla a partir de ahora.

   En un árbol, si existen, la raíz está a profundidad 0, los hijos de la raíz están a profundidad 1, los nietos de la raíz están a profundidad 2, etcétera.

   Diseña un algoritmo no recursivo, con coste temporal O(n) siendo n la cantidad de nodos del árbol, para mostrar por niveles el contenido de todos los nodos de un árbol binario, es decir, de menor a mayor profundidad: debe mostrar primero el contenido de la raíz, después el de los nodos que están a profundidad 1, después el de los nodos que están a profundidad 2, y así sucesivamente.

   Por ejemplo, si tenemos el siguiente árbol, debemos mostrar < 37 32 75 4 38 84 23 63 >.

   

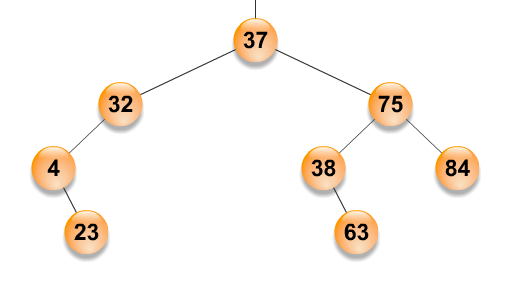
   Impleméntalo añadiendo el siguiente método público a la clase Conjunto:

   void mostrarPorNiveles() const;
   	      

   Ayuda con C++: colas

   Para resolver este problema, te puede resultar útil hacer uso de una cola.

   Para realizar la implementación, puedes usar la clase queue de la biblioteca estándar de C++.

   Mira estos ejemplos, y observa que los métodos básicos de la clase queue de los que se hace uso ahí se utilizan igual en los tres casos (en el tema siguiente veremos que, con colas de prioridad, habrá que hacer algo más):

   • ejemplo de uso de una cola de enteros

   • ejemplo de uso de una cola de objetos

   • ejemplo de uso de una cola de punteros

   Solución

8. Resuelve este ejercicio tras haber entendido la solución del anterior.

   Diseña un algoritmo cuya entrada sean un árbol binario y un entero p, y cuya salida sea un booleano que indique si existe algún nodo que esté a profundidad exactamente p. Puede suceder que el árbol esté vacío.

   Al igual que en el ejercicio anterior, considera que en un árbol, si existen, la raíz está a profundidad 0, los hijos de la raíz están a profundidad 1, los nietos de la raíz están a profundidad 2, etcétera.

   Implementa el algoritmo añadiendo el siguiente método público a la clase Conjunto:

   bool verificarProfundidad(int) const;
   	      

   1. Resuelve el problema de forma recursiva.

   2. Resuelve el problema de forma no recursiva.

   Analiza el coste temporal y el coste espacial de cada solución en función de p (no en función de la talla del árbol), sin contar el coste espacial del propio árbol.

   Solución

   Prueba de la solución

9. En un árbol AVL inicialmente vacío se insertan los siguientes datos, en este orden: 9, 8, 1, 2, 3, 4, 5, 6 y 7. Dibuja el árbol resultante tras cada inserción. Dibuja el resultado de eliminar el 3 y después el 2 a partir del último árbol.

   Vídeo de la solución (secuencia de inserciones).

   Repite el ejercicio empleando alguna de las animaciones recomendadas en el apartado Recursos.

   Compara el árbol AVL y el árbol binario de búsqueda que se obtienen con esa secuencia de operaciones. Para ello, puedes utilizar también las animaciones.

   Sigue realizando ejercicios como este, con otros datos inventados por ti, para conocer bien los algoritmos de inserción y eliminación en árboles AVL.

10. Responde las siguientes preguntas sobre el siguiente árbol AVL. Verifica tus soluciones, cuando sea posible, empleando alguna de las animaciones recomendadas en el apartado Recursos.

    

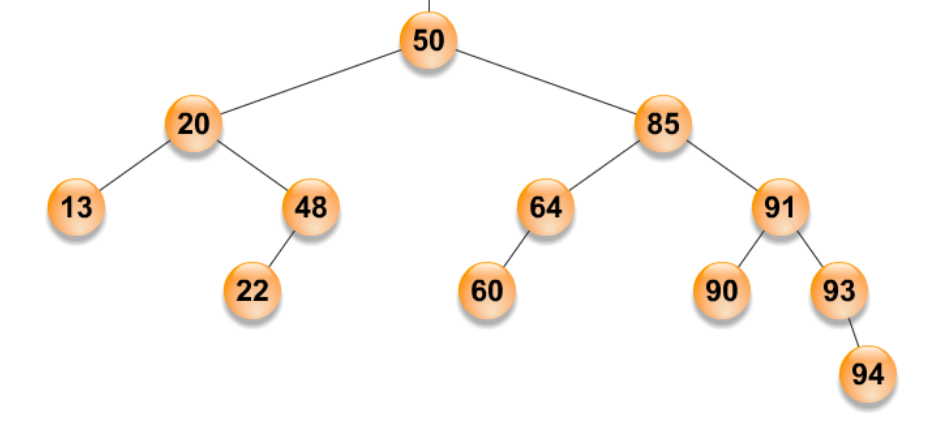
    1. Propón una secuencia de operaciones de inserción que, partiendo de un árbol vacío, dé como resultado ese árbol sin realizar ninguna rotación.

    2. Clase de teoría TE1 10/10

       ¿Qué rotaciones provoca la eliminación del 13? Dibuja el resultado.

    3. Observa que el árbol inicial tiene talla 12 y altura 4. ¿Hay alguna forma de obtener un árbol AVL de menor talla con esa misma altura?

    4. ¿Cuántos elementos habría que añadir como mínimo al árbol AVL inicial para obtener un árbol AVL de altura 5? Propón una secuencia de operaciones de inserción que lo consiga.

       Ayuda

11. 1. Suponiendo que Multiconjunto internamente utiliza un árbol binario de búsqueda (como Conjunto en el ejercicio 1 pero modificado para aceptar elementos duplicados), considera el siguiente algoritmo de ordenación, que consiste en insertar los datos a ordenar en el árbol y a continuación realizar un recorrido en inorden del mismo para obtenerlos ordenados (como en la solución del ejercicio 2.g):

       void ordenar(vector<int> & v) {
       
          Multiconjunto multiconjunto;
       
          for (int dato : v)
             multiconjunto.insertar(dato);
       
          v = multiconjunto.obtenerOrdenados();
       
       }
       		  

       ¿Cuáles son los costes temporal y espacial de ese algoritmo?

       Solución

       Prueba del algoritmo

    2. Considera de nuevo el algoritmo de ordenación del apartado anterior. Si en vez de un árbol binario de búsqueda se emplea un árbol AVL, el algoritmo se denomina AVL Sort. ¿Cúales son sus costes temporal y espacial en ese caso?

       Solución

12. [Fuente: adaptación del ejercicio 4.35 del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss]

    Implementa el constructor de la siguiente clase ArbolAVL:

    class ArbolAVL {
    
       struct Nodo {
          int dato;
          int altura;
          Nodo * izquierdo;
          Nodo * derecho;
       };
    
       Nodo * raiz;
    
       // ...
    
     public:
    
       ArbolAVL(int);
    
    };
    	      

    El constructor recibe un entero que es la altura que queremos que tenga el árbol, y debe crear un árbol AVL con la mínima cantidad posible de nodos para esa altura. En los nodos puedes poner los datos que quieras, pero deben ser diferentes y cumplir la relación de orden de los árboles AVL (que es la de los árboles binarios de búsqueda). Además cada nodo debe tener un atributo con la altura del subárbol del que es raíz. El coste temporal de tu solución debe ser O(n) siendo n la cantidad de nodos.

    Solución

    Prueba de la solución

13. Clase de prácticas LA2 y LA4 15/10, LA1 y LA3 17/10

    [Fuente: adaptación del ejercicio 4.48 del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss]

    El tiempo estimado de resolución de este ejercicio completo es de 2 horas.

    Este es un ejercicio que requiere pensar bastante para diseñar el algoritmo antes de implementarlo. Lo discutiremos en clase.

    Partiendo de nuevo de la implementación Conjunto/VersionInicial y realizando las modificaciones que consideres conveniente, añade un método público que reciba un entero k y devuelva el k-ésimo menor elemento del conjunto (contando desde 0).

    int buscarKesimo(int) const;
    	      

    Por ejemplo, si el conjunto contiene los datos {41, 62, 23, 34, 15, 56} entonces el 0-ésimo menor elemento es 15, el 3-ésimo menor elemento es 41, el 5-ésimo menor elemento es 62, etc. Debes lanzar una excepción si k es negativo o mayor o igual que la talla del conjunto.

    El coste temporal de buscarKesimo debe ser O(h) siendo h la altura del árbol. Como tenemos un árbol binario de búsqueda no equilibrado, eso es O(n); pero si cambiásemos el árbol por un árbol AVL, el coste temporal de buscarKesimo debería ser O(log n).

    Puedes añadir atributos y hacer modificaciones en otros métodos solamente si ello no afecta a su coste temporal: si tenían coste temporal O(h), deben seguir teniendo ese coste.

    Antes de empezar a programar, debes encontrar una solución al problema con el coste temporal que se pide. Es un reto difícil que abordaremos en clase. Tras haberlo intentado, si no se te ocurre ninguna solución, mira esta ayuda. Si necesitas más ayuda, puedes consultar el apartado 19.2 "Estadísticas de orden" del libro "Estructuras de datos en Java" (2013) de M. A. Weiss o el apartado 18.2 "Búsqueda por posición en el orden" de "Estructuras de datos en Java" (2000) del mismo autor (esto no aparece resuelto en la versión en C++ que utilizamos habitualmente).

    Además de realizar tus propias pruebas, puedes utilizar este programa TestKesimo.cpp para probar tu solución (debe producir esta salida TestKesimo.salida; puedes utilizar diff o sdiff en un terminal para comparar tu salida con esa):

    wget http://www3.uji.es/~vjimenez/AED/TEMA3/Conjunto/kesimo/TestKesimo.cpp
wget http://www3.uji.es/~vjimenez/AED/TEMA3/Conjunto/kesimo/TestKesimo.salida
g++ TestKesimo.cpp Conjunto.cpp
./a.out > misalida
diff TestKesimo.salida misalida
sdiff TestKesimo.salida misalida

    Si trabajas con OnlineGDB, para redirigir la salida hacia un fichero puedes introducir run > misalida en su Command line. Con eso, el botón Run te abrirá el fichero misalida en una nueva pestaña y luego lo podrás descargar con el botón Download Code.

    Opcionalmente, implementa dos versiones del método buscarKesimo: una recursiva y una no recursiva.

    Solución con ejemplos de errores

    Prueba de la solución