Tema 3: Análisis sintáctico - Ejercicios de modelado LL(1) y RLL(1)
Solución del ejercicio M7
Apartado M7.1
Es falso. Se puede demostrar con el siguiente contraejemplo:
<A> -> a | <B>
<B> -> a b
Para esta gramática incontextual obtenemos la siguiente tabla de análisis:
Producciones <A> ->  |
Anulable() |
Primeros() |
Siguientes(<A>) |
|---|---|---|---|
| 1. <A> -> a | no | a | $ |
| 2. <A> -> <B> | no | a | |
| 3. <B> -> a b | no | a | $ |
| Tabla de análisis | $ | a | b |
|---|---|---|---|
| <A> | 1, 2 | ||
| <B> | 3 |
Podemos observar que en esta tabla hay conflictos, lo cual indica que la gramática no es LL(1), a pesar de que no tiene recursión por la izquierda ni prefijos comunes.
Apartado M7.2
Es falso. Se puede demostrar con el siguiente contraejemplo:
<A> -> <A> a |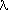 
Esta gramática incontextual no es LL(1), por tener recursión por la
izquierda (ver solución del
ejercicio A5). Y tampoco es ambigua, porque todas las cadenas del
lenguaje son de la forma an con n >= 0, y
para cada una de ellas tenemos una única derivación posible, en la que
se aplica n veces la producción <A> -> <A>
a (pues cada vez que la aplicamos generamos una
a más) y una vez, al final, la producción
<A> -> .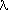
Apartado M7.3
Es cierto. Un esbozo de la demostración podría ser el siguiente.
Supongamos que la gramática es ambigua. Por tanto, existe alguna
cadena s1 s2 ... sn del lenguaje que
tiene dos derivaciones a izquierdas diferentes. Esas dos derivaciones
difieren a partir de un paso de derivación en el que, tras haber
generado s1
s2 ... sj <A> ... (con 0 <= j <= n), se
aplican producciones diferentes, <A> -> en una y <A> -> 
en otra. Pero al final ambas
derivaciones han de llegar a s1 s2
... sn $. Por las definiciones de primeros y siguientes, de
ahí se deduce que el terminal a que hay a continuación
de sj (o a = $ si j = n) es
uno de los primeros de , o bien es uno
de los siguientes de y es anulable; y del mismo modo, se deduce
que es uno de los primeros de , o es
uno de los siguientes de y es anulable. En cualquier caso, por la
forma de construir la tabla de análisis, eso lleva a que en la celda
M[<A>, a] tengamos un conflicto entre y . Y si la
gramática es LL(1), eso no puede suceder.