Tema 3: Análisis sintáctico - Ejercicios de modelado LL(1) y RLL(1)

Solución del ejercicio M1

Apartado M1.1

Producciones <A> ->	Anulable()	Primeros()	Siguientes(<A>)
1. <S> -> a <S> b	no	a	$ b
2. <S> -> a b	no	a

Tabla de análisis	$	a	b
<S>		1, 2

Podemos observar que hay un conflicto que indica que la gramática G₁ no es LL(1): al analizar <S>, si el símbolo de anticipación fuese a no sabríamos si aplicar la producción 1 o la producción 2.

Apartado M1.2

Para eliminar prefijos comunes, podemos realizar una factorización por la izquierda. En este caso, obtenemos la siguiente gramática con partes derechas regulares G₂, equivalente a G₁:

<S> -> a (<S> b | b)

Y eliminando la disyunción sustituyéndola por un nuevo no terminal obtenemos la siguiente gramática incontextual G₂₂, equivalente a G₂ y a G₁:

<S> -> a <B>
<B> -> <S> b | b

Para G₂₂ obtenemos la siguiente tabla de análisis:

Producciones <A> ->	Anulable()	Primeros()	Siguientes(<A>)
1. <S> -> a <B>	no	a	$ b
2. <B> -> <S> b	no	a	$ b
3. <B> -> b	no	b

Tabla de análisis	$	a	b
<S>		1
<B>		2	3

Podemos observar que en esta tabla no hay conflictos, lo cual indica que la gramática incontextual G₂₂ es LL(1), y por tanto que la gramática con partes derechas regulares G₂ es RLL(1).

Una solución alternativa, igualmente válida, sería la siguiente:

<S> -> a <T> b
<T> -> a <T> b |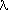

Podemos comprobar que es LL(1) construyendo su tabla de análisis (observa bien que aquí no tenemos lo que se denomina prefijos comunes):

Producciones <A> ->	Anulable()	Primeros()	Siguientes(<A>)
1. <S> -> a <T> b	no	a	$
2. <T> -> a <T> b	no	a	b
3. <T> ->	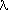si

Tabla de análisis	$	a	b
<S>		1
<T>		2	3

Apartado M1.3

Una posible solución sería la siguiente:

<S> -> a <T> b
<T> -> a <T> b | c

Esta gramática es LL(1), como se puede comprobar construyendo su tabla de análisis:

Producciones <A> ->	Anulable()	Primeros()	Siguientes(<A>)
1. <S> -> a <T> b	no	a	$
2. <T> -> a <T> b	no	a	b
3. <T> -> c	no	c

Tabla de análisis	$	a	b	c
<S>		1
<T>		2		3

Se puede llegar a otra solución partiendo de la siguiente gramática, que no es LL(1) por tener prefijos comunes:

<S> -> a <S> b | a c b

Factorizando obtenemos la siguiente gramática RLL(1):

<S> -> a (<S> b | c b)

Y reemplazando ahora la disyunción por un nuevo no terminal obtenemos la siguiente gramática LL(1):

<S> -> a <B>
<B> -> <S> b | c b

Apartado M1.4

Una posible solución sería la siguiente gramática LL(1):

<S> -> d a <T> b d
<T> -> a <T> b | c

Se puede llegar a otra solución partiendo de la siguiente gramática, que no es LL(1) por tener prefijos comunes:

<D> -> d <S> d
<S> -> a <S> b | a c b

Factorizando prefijos comunes y reemplazando la disyunción por un nuevo no terminal como en el apartado (3) obtenemos la siguiente gramática LL(1):

<D> -> d <S> d
<S> -> a <B>
<B> -> <S> b | c b

Se puede comprobar fácilmente que las últimas soluciones son LL(1), construyendo sus tablas de análisis como en los ejemplos anteriores.

---