Tema 3: Análisis sintáctico - Ejercicios de modelado LL(1) y RLL(1)

Solución del control de análisis sintáctico del grupo TE2 del curso 2009/2010

Ejercicio 3 (0.30 puntos)

El resultado de escribir una gramática que sea RLL(1) y genere el mismo lenguaje que G₁, teniendo en cuenta las prioridades y asociatividades de los operadores para evitar la ambigüedad, podría ser la siguiente gramática con partes derechas regulares G₃:

<Expresión> -> <Término> ( potencia <Expresión> )?
<Término> -> <Base> ( factorial )*
<Base> -> número | abreParéntesis <Expresión> cierraParéntesis | signo <Base>

Para demostrar que G₃ es RLL(1) podemos construir la tabla de análisis de la siguiente gramática incontextual G₄, resultado de eliminar partes derechas regulares con las transformaciones que hemos estudiado (utilizamos las iniciales de los símbolos de la gramática como abreviaturas):

Producciones <A> ->	Anulable()	Primeros()	Siguientes(<A>)
1. <E> -> <T> <P>	no	n a s	$ c
2. <P> -> p <E>	no	p	$ c
3. <P> ->	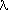sí
4. <T> -> <B> <F>	no	n a s	$ c p
5. <F> -> f <F>	no	f	$ c p
6. <F> ->	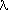sí
7. <B> -> n	no	n	$ c p f
8. <B> -> a <E> c	no	a
9. <B> -> s <B>	no	s

Tabla de análisis	$	p	f	n	a	s	c
<E>				1	1	1
<P>	3	2					3
<T>				4	4	4
<F>	6	6	5				6
<B>				7	8	9

Podemos observar que no hay conflictos en esta tabla, y por tanto la gramática G₄ es LL(1) y la gramática G₃ es RLL(1).

Ejercicio 2 (0.05 puntos)

G₂ no genera el mismo lenguaje que G₁. Por ejemplo, la cadena número factorial factorial pertenece a L(G₁) y no pertenece a L(G₂).

Ejercicio 1 (0.15 puntos)

G₂ es ambigua porque hay al menos una cadena que tiene dos árboles de derivación diferentes: signo número factorial.

        <E>           <E>
         |             |
         |             |
        <T>           <T>
        /|\           / \
       / | \         /   \
      s <T> f       s    <T>
         |                /\
         |               /  \
         n              n    f

G₂ no es RLL(1), porque no puede serlo si es ambigua.

Observaciones

Con esta prueba se ha pretendido valorar quién tiene la capacidad y autonomía necesarias para resolver ejercicios de modelado sintáctico como los propuestos en la última parte del tema 3 y en la práctica 2. No basta con haber llegado a uno de los objetivos previos ni con reutilizar soluciones conocidas.

Quien supiese escribir G₃ podía resolver los ejercicios 1 y 2 viendo que G₂ no es la gramática que él escribiría y viendo las consecuencias de las dos diferencias importantes: cambiar signo <Base> por signo <Término>, y cambiar ( factorial )* por ( factorial )?.

Quien viese que G₂ es ambigua se podía ahorrar el tiempo necesario para demostrar que no es RLL(1) construyendo la correspondiente tabla de análisis.

Alternativamente, se podía demostrar que G₂ no es RLL(1) construyendo la tabla de análisis de la siguiente gramática incontextual G₅, teniendo en cuenta que perder el tiempo haciendo eso iba a restar tiempo a otras partes del control.

Producciones <A> ->	Anulable()	Primeros()	Siguientes(<A>)
1. <E> -> <T> <P>	no	n a s	$ c
2. <P> -> p <E>	no	p	$ c
3. <P> ->	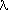sí
4. <T> -> <B> <F>	no	n a s	$ c p f
5. <F> -> f	no	f	$ c p f
6. <F> ->	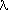sí
7. <B> -> n	no	n	$ c p f
8. <B> -> a <E> c	no	a
9. <B> -> s <T>	no	s

Tabla de análisis	$	p	f	n	a	s	c
<E>				1	1	1
<P>	3	2					3
<T>				4	4	4
<F>	6	6	5, 6				6
<B>				7	8	9

El conflicto entre las producciones 5 y 6 en la celda [<F>,f] , que muchos estudiantes no encontraron, implica que G₅ no es LL(1) y por tanto que G₂ no es RLL(1).

Otra forma de ahorrarse esta tabla de análisis sería demostrar que G₅ es ambigua, de lo que se deduce que G₅ no es LL(1) y por tanto que G₂ no es RLL(1); y eso se puede hacer adaptando a G₅ el ejemplo de los dos árboles de derivación anteriores.

Ejemplos de errores

Esto que sigue son ejemplos de afirmaciones incorrectas realizadas por algunos estudiantes en su solución, que indican en muchos casos su falta de rigor y de dedicación al estudio, la empanada mental con la que acudieron a este examen, y quizás la falta de preparación con la que salen de la asignatura II20:

1. G₂ no genera el mismo lenguaje que G₁ porque G₁ permite tener <Expresión> a la izquierda de potencia mientras que G₂ sólo permite <Término>.

2. G₂ sí genera el mismo lenguaje que G₁ pero G₁ es ambigua y además no respeta las prioridades ni las asociatividades de los operadores.

3. G₂ no es RLL(1) porque es recursiva por la izquierda.

4. G₂ es RLL(1) ya que no es ambigua ni tiene recursión por la izquierda.

5. Viendo el conflicto de la tabla de análisis de G₂ podemos deducir que no es RLL(1) y por lo tanto que es ambigua.

6. Eliminando prefijos comunes y recursividad por la izquierda en G₁ obtenemos G₂ y por lo tanto generan el mismo lenguaje.

7. G₁ y G₂ no generan el mismo lenguaje porque G₂ no respeta el orden de precedencia entre signo y factorial.

8. G₁ y G₂ no generan el mismo lenguaje porque G₂ acepta un número sólo y G₁ no lo acepta ya que ésta obliga a tener una potencia.

9. G₁ y G₂ no generan el mismo lenguaje porque en G₁ todos los operadores tienen la misma prioridad y en G₂ el operador potencia es el que menos prioridad tiene.

10. Teniendo en cuenta que el conflicto en la tabla de análisis de G₂ se halla en la producción del factorial y que éste es opcional, no se encuentra más de un árbol de derivación, por lo que no es ambigua.

11. G₂ no genera el mismo lenguaje que G₁ puesto que las prioridades de los operadores no son las mismas.

12. G₂ no genera el mismo lenguaje que G₁ puesto que en G₂ factorial no va precedido de <Expresión>.

13. G₂ no es ambigua ya que no he encontrado ninguna cadena que tenga dos o más árboles de derivación.

14. G₂ no genera el mismo lenguaje que G₁ puesto que, por ejemplo, G₂ no me permite poner <Expresión> potencia <Expresión>.

15. G₂ no genera el mismo lenguaje ya que factorial es más prioritario que signo.

16. G₂ es RLL(1) ya que no hay recursión por la izquierda ni prefijos comunes directos o indirectos. Por lo tanto tampoco es ambigua.

17. Como G₃ es RLL(1) y ambas gramáticas son equivalentes, G₂ es RLL(1).

18. G₂ no es ambigua porque la potencia se calcula correctamente (binaria y asociativa por la derecha), el cambio de signo también (unario y prefijo) y el factorial también (unario y postfijo).

19. G₂ no genera el mismo lenguaje que G₁ porque G₁ es ambigua (por tener <Expresión> -> <Expresión> potencia <Expresión>).

20. G₂ no genera el mismo lenguaje que G₁ porque G₂ no reconoce por ejemplo signo número potencia <Expresión> y G₁ sí.

21. G₂ no genera el mismo lenguaje porque en G₂ antes del factorial no podemos tener una expresión que lleve potencia a no ser que vaya entre paréntesis, y en G₁ sí.

22. G₂ no es ambigua puesto que para una entrada sólo podemos escoger una producción y no tenemos factores comunes con ésta.

23. Como G₂ es LL(1) podemos decir que es RLL(1).

24. G₂ no es RLL(1) ya que, en el caso de que reciba una cadena que comience por número, a priori no se sabe si debe tomar <Expresión> -> <Término> o <Expresión> -> <Término> potencia <Expresión>, ya que ambas contendrán como primeros el elemento número.

25. G₂ no genera el mismo lenguaje ya que por ejemplo el cambio de signo no se aplica a <Expresión>, tan sólo a <Término>, por tanto no se podría cambiar de signo a una potencia como sí lo permite G₁.

26. G₂ no es RLL(1) porque no es LL(1). Y no es LL(1) porque no podrás tener dos factoriales seguidos.

Es una buena colección de contrasentidos. Puede ser muy recomendable pensar en qué se ha equivocado cada uno de esos estudiantes.

---