Algoritmos y Estructuras de Datos (VJ1215)

Como primer ejemplo de algoritmo voraz vamos a estudiar el algoritmo de Huffman, con el que realizamos también las prácticas del tema 4 para trabajar con colas de prioridad.

Consulta el siguiente apartado del capítulo 10 "Algorithm Design Techniques" del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss aparece en:

• 10.1.2 Huffman Codes

En el tema 6 "Algoritmos fundamentales sobre grafos" veremos otros dos ejemplos de algoritmos voraces:

• Algoritmo de Dijkstra (para resolver el problema del camino óptimo).

• Algoritmo de Prim (para resolver el problema del árbol de recubrimiento óptimo).

1. 1. Aplica el algoritmo de Huffman con estos datos y dibuja el árbol de Huffman resultante:

      Carácter	a	b	c	d	e	f	g	h
      Frecuencia	80	30	40	20	70	60	10	50

   2. Calcula cuántos bits ahorramos empleando la codificación obtenida en vez de 3 bits por carácter si queremos codificar un mensaje en el que aparecen esos caracteres en esas cantidades.

      Solución

2. Los biólogos utilizan los caracteres A, C, G y T para denotar Adenina, Citosina, Guanina y Timina, respectivamente. De ese modo una secuencia de ADN queda representada como una secuencia formada por esos caracteres, por ejemplo GATTACA. Si cada carácter se codificase con 8 bits, una secuencia de longitud n ocuparía 8n bits. Teniendo en cuenta que solo hay 4 caracteres posibles, podríamos emplear 2 bits para codificarlos, reduciendo así a 2n la ocupación de una secuencia de n caracteres.

   1. Supongamos que sabemos que en el ADN hay un 40 % de Adenina, un 10 % Citosina, un 10 % de Guanina y un 40 % de Timina. ¿Sabrías utilizar esa información para reducir más la ocupación de las secuencias de ADN? Ilústralo obteniendo la codificación de cada carácter y calculando, con la codificación obtenida, cuál sería la ocupación de una secuencia de n caracteres que tenga esas frecuencias.
   2. ¿Qué relación tiene ese problema con los árboles binarios?
   3. ¿Qué relación tiene ese problema con las colas de prioridad?
   4. ¿Qué relación tiene ese problema con las estrategias algorítmicas?

   Solución

3. Analiza el coste temporal en el peor caso del algoritmo de Huffman cuando se aplica a un alfabeto que tiene n caracteres, suponiendo que la cola de prioridad que utiliza el algoritmo se implementa empleando:

   1. Un vector no ordenado.

   2. Un vector ordenado.

   3. Un árbol binario de búsqueda.

   4. Un árbol AVL.

   5. Un montículo binario.

   Solución

4. Aplicando el algoritmo de Huffman hemos obtenido este resultado:

   Carácter	a	e	i	o	u
   Código	0	10	110	1110	1111

   Propón una tabla de frecuencias a partir de la cual se haya podido obtener eso y dibuja el árbol de Huffman.

Complementa la clase de teoría estudiando los siguientes apartados del capítulo 7 "Sorting" y del capítulo 10 "Algorithm Design Techniques" del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss.

• 7.6 Mergesort
• 10.2 Divide and conquer
  • 10.2.1 Running Time of Divide and Conquer Algorithms
  • 10.2.2 Closest-Points Problem

Debes aprender a aplicar el denominado Teorema Maestro tal como se formula en los teoremas 10.6 y 10.7 del apartado 10.2.1; entender las demostraciones de esos teoremas es opcional.

El Master Theorem Solver de Nayuki Minase te puede resultar de ayuda para comprobar tus soluciones.

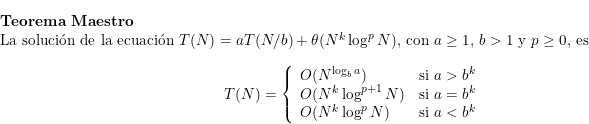
1. Supongamos que queremos resolver el problema de encontrar el máximo en un vector de talla mayor que cero empleando la estrategia Divide y Vencerás. Analiza el coste temporal de las siguientes implementaciones, empleando el Teorema Maestro.

   1. Clase de teoría TE1 21/11

      Un primer programador ha realizado la siguiente implementación:

      int maximo(const vector<int> & v) { // Suponemos v.size() >= 1
         return maximo(v, 0, v.size() - 1);
      }
      int maximo(const vector<int> & v, int inicio, int fin) {
         if (inicio == fin)
            return v[inicio];
         else {
            int mitad = (inicio + fin) / 2;
            int maximoIzquierda = maximo(v, inicio, mitad);
            int maximoDerecha = maximo(v, mitad + 1, fin);
            if (maximoIzquierda >= maximoDerecha)
               return maximoIzquierda;
            else
               return maximoDerecha;
         }
      }
      		  

      Solución

   2. Clase de teoría TE1 21/11

      Un segundo programador hace lo que se muestra a continuación, en vez de trabajar con un solo vector como en el apartado a:

      int maximo(const vector<int> & v) { // Suponemos v.size() >= 1
         if (v.size() == 1) return v[0];
         int mitad = v.size() / 2;
         vector<int> izquierda(mitad);
         for (int i = 0; i < mitad; i++)
            izquierda[i] = v[i];
         vector<int> derecha(v.size() - mitad);
         for (int i = mitad, j = 0; i < v.size(); i++, j++)
            derecha[j] = v[i];
         int maximoIzquierda = maximo(izquierda);
         int maximoDerecha = maximo(derecha);
         if (maximoIzquierda >= maximoDerecha)
            return maximoIzquierda;
         else
            return maximoDerecha;
      }
      		  

      Solución

   3. Clase de teoría TE1 21/11

      Un tercer programador implementa el algoritmo utilizando un solo vector como en el primer apartado pero ahorrándose las variables maximoIzquierda y maximoDerecha, como se muestra a continuación:

      int maximo(const vector<int> & v) { // Suponemos v.size() >= 1
         return maximo(v, 0, v.size() - 1);
      }
      int maximo(const vector<int> & v, int inicio, int fin) {
         if (inicio == fin)
            return v[inicio];
         else {
            int medio = (inicio + fin) / 2;
            if ( maximo(v, inicio, medio) >= maximo(v, medio + 1, fin) )
      	 return maximo(v, inicio, medio);
            else
      	 return maximo(v, medio + 1, fin);
         }
      }
      		  

      Solución

   4. Un cuarto programador combina lo que hacen los dos anteriores:

      int maximo(const vector<int> & v) { // Suponemos v.size() >= 1
         if (v.size() == 1) return v[0];
         int mitad = v.size() / 2;
         vector<int> izquierda(mitad);
         for (int i = 0; i < mitad; i++)
            izquierda[i] = v[i];
         vector<int> derecha(v.size() - mitad);
         for (int i = mitad, j = 0; i < v.size(); i++, j++)
            derecha[j] = v[i];
         if (maximo(izquierda) >= maximo(derecha))
            return maximo(izquierda);
         else
            return maximo(derecha);
      }
      		  

      Solución

   5. Finalmente, un quinto programador propone lo siguiente:

      int maximo(const vector<int> & v, int inicio, int fin) { // Suponemos v.size() >= 1
         if (fin - inicio <= 3) {
            int aux = v[inicio];
            for (int i = inicio + 1; i <= fin; i++)
               aux = max(aux, v[i]);
            return aux;
         } else {
            int medio = (inicio + fin) / 2;
            int cuartoIzquierda = (inicio + medio) / 2;
            int cuartoDerecha = (medio + 1 + fin) / 2;
            int aux = maximo(v, inicio, cuartoIzquierda);
            aux = max(aux, maximo(v, cuartoIzquierda + 1, medio));
            aux = max(aux, maximo(v, medio + 1, cuartoDerecha));
            aux = max(aux, maximo(v, cuartoDerecha + 1, fin));
            return aux;
         }
      }
      int maximo(const vector<int> & v) {
         return maximo(v, 0, v.size() - 1);
      }
      		  

      Solución

2. Búsqueda binaria

   Utiliza el Teorema Maestro para analizar esta implementación de la búsqueda binaria recursiva que vimos en el tema 1.

   int busquedaBinariaRecursiva(const vector<int> & v, int dato, int inicio, int fin) {
      if (inicio <= fin) {
         int medio = (inicio + fin) / 2;
         if (v[medio] < dato)
            return busquedaBinariaRecursiva(v, dato, medio + 1, fin);
         else if (v[medio] > dato)
            return busquedaBinariaRecursiva(v, dato, inicio, medio - 1);
         else
            return medio;
      }
      return -1;
   }
   
   
   int busquedaBinariaRecursiva(const vector<int> & v, int dato) {
      return busquedaBinariaRecursiva(v, dato, 0, v.size() - 1);
   }
   	      

   Solución

3. Exponenciación binaria

   1. El algoritmo de exponenciación binaria, que vimos en el ejercicio 10 del tema 1, es también un ejemplo de aplicación de la estrategia Divide y Vencerás. Considera la siguiente versión del algoritmo. Expresa su coste temporal empleando una relación de recurrencia y obtén su solución empleando el Teorema Maestro.

      float potencia(float x, int n) {
      
         if (n == 0)
            return 1;
      
         float y = potencia(x, n / 2);
      
         if (n % 2 == 1)
            return x * y * y;
      
         return y * y;
      
      }
      		  

      Solución

   2. Utiliza el Teorema Maestro para analizar cómo cambiaría el tiempo de ejecución si resolviésemos así el mismo problema:

      float potencia(float x, int n) {
      
         if (n == 0)
            return 1;
      
         if (n % 2 == 1)
            return x * potencia(x, n / 2) * potencia(x, n / 2);
      
         return potencia(x, n / 2) * potencia(x, n / 2);
      
      }
      		  

      Solución

4. Encuentra la solución de las siguientes relaciones de recurrencia empleando el Teorema Maestro.

   1. T(n) = 7 T(n/2) + O(n²)
   2. T(n) = 8 T(n/2) + O(n²)
   3. T(n) = 8 T(n/4) + O(n²)
   4. T(n) = 4 T(n/2) + O(n²)
   5. T(n) = 2 T(n/2) + O(log n)
   6. T(n) = T(n/2) + O(log n)
   7. T(n) = T(n/2) + O(n log n)

   Comprueba si tus soluciones son correctas viendo si coinciden con las del Master Theorem Solver de Nayuki Minase.

   Prueba tú mismo otros ejemplos si lo consideras conveniente, hasta saber aplicar bien el teorema.

   Recursos opcionales
   Algoritmo de Strassen para multiplicar dos matrices
   Opcionalmente, busca en el libro "Data Structures and Algorithm Analysis in C++" (2014) el apartado 10.2.4 (páginas 498-500 de la edición internacional, la que tiene la biblioteca de la UJI). Ahí se explica el algoritmo de Strassen para multiplicar matrices, cuyo tiempo de ejecución cumple la relación de recurrencia del apartado (a). En castellano puedes encontrar eso mismo en la edición "Estructuras de datos y algoritmos" (1995), páginas 394-397.

5. Mergesort

   Clase de teoría TE1 21/11

   Analiza el coste temporal del algoritmo de ordenación Mergesort empleando el Teorema Maestro.

   Solución

6. Problema del par de puntos más cercanos

   Clase de teoría TE1 21/11
   Clase de prácticas LA2 y LA4 26/11, LA1 y LA3 28/11

   El tiempo estimado de resolución de este ejercicio completo, tras la explicación del algoritmo en clase, es de 3 horas.

   Imagina que estás desarrollando un videojuego en el que puede haber muchos objetos que tienen unas coordenadas 2D y debes encontrar los dos objetos más próximos entre si, por ejemplo para prevenir una posible colisión entre ellos (esto también tiene aplicación práctica en sistemas de control de tráfico aéreo) o para que esos dos personajes del videojuego sean los que luchen, se emparejen, etc.

   1. Ejercicio opcional (hazlo si no estás seguro de saber hacerlo)

      Implementa en C++ una función que reciba un vector de n puntos en el plano y devuelva la distancia entre los dos puntos más cercanos empleando el algoritmo de fuerza bruta que calcula todas las distancias posibles con coste O(n²).

      Ayuda con C++: pair para representar puntos

      Si lo deseas puedes implementar y usar tu propia clase Punto, o también puedes hacer uso de la clase pair para representar puntos. Si optas por lo segundo, puedes emplear typedef para llamarle Punto:

      typedef pair<float, float> Punto;
      Punto p1 = {2, 3}, p2 = {5, 7};
      vector<Punto> puntos = {p1, p2, Punto(3, 4), Punto(4, 4), Punto(4, 4), Punto(5,7)};
      if (p1 == p2) ...
      if (p1 < p2) ...
      		    

      Solución

      Fichero de la solución

   2. Tanto si has realizado el ejercicio del apartado a como si no, entiende su solución antes de pasar a este apartado b.

      Resuelve el mismo problema del apartado a, empleando el algoritmo que emplea la estrategia Divide y Vencerás, cuyo tiempo de ejecución es O(n log n). Este algoritmo se explicó en clase de teoría y lo puedes encontrar también en el apartado 10.2.2 del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss.

      Ayuda (resumen de lo discutido en clase)

      Puedes completar este programa de prueba TestClosestPoints.cpp para que produzca esta salida TestClosestPoints.salida.

      Ayuda con C++: min

      Puedes utilizar min para calcular el mínimo de dos o de varios valores: TEMA5_min_max.cpp.

      Ayuda con C++: copiar vectores

      Para crear copias de vectores puedes mirar este otro ejemplo de uso de vector: TEMA5_vector_copiar.cpp.

      Ayuda con C++: ordenar vectores de objetos

      En el tema 1 vimos cómo utilizar sort para ordenar vectores de enteros. Si queremos ordenar vectores de objetos, también podemos utilizar sort, pero tenemos que hacer algo más para que pueda comparar dos objetos y decidir si uno es menor que otro. En esta práctica, además, necesitamos realizar dos ordenaciones, con dos criterios diferentes:

      • Para ordenar el vector de puntos por coordenada X y, en caso de empate, por coordenada Y, la clase pair ya se comporta como necesitamos, gracias a que en ella han implementado operator< que hace exactamente esa comparación. Puedes ver un ejemplo aquí al final.

        Si en vez de utilizar pair has decidido implementar tu propia clase Punto, le puedes añadir el operator< como se muestra en la clase Jugador en TEMA5_vector_de_objetos_ordenar.cpp.

      • Para ordenar el vector de puntos por coordenada Y, puedes darle a sort una función de comparación para que la utilice en vez del operator<, como se ilustra en la función mayorPuntuacion en TEMA5_vector_de_objetos_ordenar.cpp (también puedes consultar el apartado "A Function Pointer as Comparison Function" del tutorial"STL Sort Comparison Function" de Shao Voon Wong).

      Solución

      Fichero de la solución

   3. Ejercicio opcional

      Realiza una comparación experimental de ambos algoritmos, midiendo sus tiempos de ejecución al aplicarlos a vectores de puntos generados aleatoriamente. Observa la importancia de seleccionar el algoritmo más eficiente cuando hay que trabajar con grandes cantidades de datos en poco tiempo.

      Fichero de la solución

      Si no realizas la implementación, sería interesante que al menos veas estos resultados de 2014, 2021 y 2023. Observa que los tiempos se reducen al trabajar con una nueva CPU, un nuevo compilador, etc., pero la forma de la curva se mantiene.

7. Ejercicio opcional

   Algoritmo de Karatsuba para multiplicar enteros

   El algoritmo de Karatsuba resuelve el problema de multiplicar números enteros de muchos dígitos. Para ello emplea la estrategia Divide y Vencerás. Estudia la explicación que puedes encontrar en el apartado 10.2.4 del libro "Data Structures and Algorithm Analysis in C++" (2014), hasta entender el cambio que hace que el tiempo de ejecución pase de T(n)=4T(n/2)+O(n) a T(n)=3T(n/2)+O(n).

   Resuelve ambas relaciones de recurrencia empleando el Teorema Maestro y compara sus resultados.

   En castellano puedes encontrar eso mismo en la edición "Estructuras de datos y algoritmos" (1995), páginas 393-394.

En este tema partiremos de las explicaciones dadas en clase de teoría. Estudia este tema resolviendo los ejercicios propuestos. Tras intentar cada ejercicio, estudia su solución y pasa a intentar el siguiente. La bibliografía a consultar se irá indicando cuando sea necesario en los ejercicios.

Este es un tema complicado, no pretendas aprenderlo en un día, dedícale tiempo suficiente hasta la fecha de evaluación. Este curso vamos a dedicarle dos sesiones de teoría y dos sesiones de prácticas. Intenta seguir el ritmo de esas clases.

Si no puedes asistir a la primera clase de teoría de este tema, empieza estudiando el apartado 7.6 "Programación Dinámica" del libro "Estructuras de datos en Java" (2013) de M. A. Weiss, aunque no vamos a seguir exactamente ese enfoque: a lo que se explica ahí añadiremos algoritmos recursivos eficientes y más ejemplos, como irás viendo en los ejercicios.

Completa los siguientes ejercicios de forma no presencial. Incluso los que se hayan discutido en clase, resuélvelos de nuevo escribiendo tú la solución completa.

Nivel de dificultad 0

1. Clase de teoría TE1 28/11

   Este es un ejercicio preliminar para entender el uso de una tabla para guardar resultados y no repetir cálculos.

   En el tema 1 hemos visto lo ineficiente que es calcular el i-ésimo número de Fibonacci de forma recursiva como sigue (aplicando directamente esta definición recursiva):

   long long fibonacci(int i) {
   
      long long resultado;
   
      if (i <= 1)
         resultado = i;
      else
         resultado = fibonacci(i - 1)
   	          + fibonacci(i - 2);
   
      return resultado;
   
   }
   	      

   Partiendo de esa versión, resuelve el problema de la ineficiencia añadiendo una tabla de resultados para no repetir cálculos. Después modifíca la implementación para rellenar la misma tabla de forma no recursiva.

   Solución

   La animación Dynamic Programming (Fibonacci) de David Galles te puede ayudar a entender la solución. Lo que denomina "Fibonacci Memoized" es la solución recursiva eficiente y lo que denomina "Fibonacci Table" es la solución no recursiva eficiente.

El objetivo fundamental de este tema es que seas capaz de resolver ejercicios como los que se proponen a continuación. No solo por la enorme importancia del tema, también porque es un tipo de ejercicios que aparece en entrevistas de trabajo de programación. Para cada ejercicio, procede en este orden:

Nivel de dificultad 1 (sin bucles en la versión 1)

2. Clase de teoría TE1 28/11

   Considera un juego en el que cada partida tiene un diseño como el que ilustra el ejemplo de la siguiente figura.

   

   El escenario siempre está formado por una matriz rectangular de celdas. Los números indican los puntos que el jugador puede acumular superando retos en cada celda. Las dimensiones de la matriz y las puntuaciones pueden variar de una partida a otra, pero las reglas del juego son siempre las siguientes:

   • El jugador debe empezar en la celda de la esquina superior izquierda y debe llegar hasta la celda de la esquina inferior derecha.

   • Solo se permiten dos tipos de movimientos para desplazarse de una celda a otra: hacia la derecha y hacia abajo.

   • No está permitido retroceder, salir de la frontera exterior ni atravesar las celdas negras.

   Diseña, analiza sus costes e implementa un algoritmo eficiente que, a partir de la matriz puntos correspondiente a una partida, calcule la máxima cantidad de puntos que puede acumular el jugador. En la matriz puntos las celdas no atravesables (celdas negras) se representarán con valor -1 y el resto de datos indicarán la cantidad de puntos que el jugador puede obtener en cada celda.

   Como sugerencia, empieza resolviendo el problema ignorando las celdas negras y después piensa qué hacer con ellas en la solución.

   Completa este código de prueba.

   Solución 1: recursión empieza en la última celda

   Solución 2: recursión empieza en la primera celda

   Costes

3. Weighted interval scheduling

   Clase de prácticas LA2 y LA4 03/12, LA1 y LA3 05/12

   El tiempo estimado de resolución de este ejercicio, incluyendo la discusión inicial en clase, es de 1.5 horas.

   En una competición de videojuegos se programan n partidas. Para i desde 0 hasta n - 1, la partida i-ésima tiene una hora de inicio competición[i].inicio, una hora de finalización competición[i].final y un premio para el ganador competición[i].premio. Los premios son valores positivos. Los datos están ordenados de menor a mayor por hora de inicio. Un jugador tiene que decidir en qué partidas participa con el objetivo de maximizar la suma de los premios ganados y con la restricción de que no puede inscribirse en partidas cuyos horarios se solapan. Como ayuda, competición[i].primeraPosterior indica cuál es la primera de las partidas en las que podría participar después de participar en la i-ésima (si vale -1 indica que no hay ninguna).

   Por ejemplo, con los siguientes datos podría acumular 14000 ganando las partidas 1, 2 y 5, y el valor máximo que podría acumular es 15000 ganando las partidas 0 y 4:

   partida	0	1	2	3	4	5
   inicio	10	11	13	15	16	17
   final	14	12	17	17	19	18
   premio	7000	3000	9000	5000	8000	2000
   primeraPosterior	3	2	5	5	-1	-1

   Si la programación de las partidas pasase a ser la siguiente, el máximo valor acumulable sería 26000, ganando las partidas 0, 3, 6 y 7:

   partida	0	1	2	3	4	5	6	7	8
   inicio	10	11	13	15	16	17	17	18	18
   final	14	18	17	17	19	19	18	19	19
   premio	7000	3000	9000	5000	8000	2000	4000	10000	6000
   primeraPosterior	3	7	5	5	-1	-1	7	-1	-1

   Diseña, analiza sus costes e implementa un algoritmo eficiente para averiguar, dada una tabla competición como la que ilustran los dos ejemplos anteriores, cuál es la máxima suma de premios que puede acumular un jugador (puedes utilizar de la tabla los datos que quieras).

   Completa este código de prueba.

   Ayuda: solución recursiva inicial

   Solución

   Costes

   En la solución anterior, la recursión empieza en la primera partida; la solución empezando en la última partida, análoga a la del ejercicio 2 que empieza en la última celda, no podría aprovechar tan eficientemente la información que nos dan con primeraPosterior.

4. House robber

   [Este es un ejemplo de ejercicio planteado por Google en sus entrevistas para seleccionar programadores.]

   A lo largo de una calle hay n casas, numeradas de 0 a n - 1. La casa i está pegada a la casa i - 1 por la izquierda y a la i + 1 por la derecha, para i = 1, ..., n - 2. Un ladrón va a robar lo máximo que pueda en estas casas, pero no puede robar en dos casas que estén pegadas porque el dueño de una casa robada avisará a sus vecinos izquierdo y derecho. Sea valoresCasas un vector de talla n en el que valoresCasas[i] es el valor que puede conseguir robando la casa i-ésima, para i = 0, ..., n - 1.

   Diseña, analiza sus costes e implementa un algoritmo eficiente que permita averiguar, dado valoresCasas, cuál es el máximo valor que puede acumular el ladrón.

   Por ejemplo, si hay cuatro casas con valoresCasas = {3000, 6000, 7000, 5000}, el valor máximo que puede acumular es 11000 robando las casas 1 y 3. Con valoresCasas = {6000, 10000, 3000, 15000, 4000, 2000, 8000, 5000} el resultado sería 33000, robando 10000, 15000 y 8000.

   Completa este código de prueba.

   Ayuda: solución recursiva inicial

   Solución

   Costes

   En la solución anterior, la recursión empieza en la última casa; se podría resolver análogamente empezando en la primera casa, como ilustran las dos soluciones del ejercicio 2.

5. House coloring

   A lo largo de una playa hay n ≥ 1 casas, numeradas de 0 a n - 1. La casa k está pegada a la casa k - 1 por la izquierda y a la k + 1 por la derecha, para k = 1, ..., n - 2. Queremos pintar cada casa de un color de modo que no haya dos casas pegadas que tengan el mismo color, y podemos elegir entre tres colores. Nos dan una matriz de valores reales positivos costePintura en la que costePintura[c][k] es el coste de pintar de color c la casa k, para c = 0, ..., 2 y para k = 0, ..., n - 1.

   Diseña, analiza sus costes e implementa un algoritmo eficiente que calcule cuál es el mínimo coste total de pintar todas las casas. La cantidad de casas será uno de los datos de entrada al algoritmo, a diferencia de la cantidad de colores, que es constante y vale 3.

   Por ejemplo, con los siguientes datos:

   					casas
   		0	1	2	3	4	5	6
   	0	300	600	200	1000	1500	500	900
   colores	1	400	1600	400	700	1200	400	200
   	2	500	1300	600	100	300	500	800

   el resultado sería 3300, correspondiente a elegir las siguientes celdas coloreadas:

   					casas
   		0	1	2	3	4	5	6
   	0	300	600	200	1000	1500	500	900
   colores	1	400	1600	400	700	1200	400	200
   	2	500	1300	600	100	300	500	800

   Completa este código de prueba.

   Solución 1

   Solución 2

   Costes

   Aprende más ayudando a otros estudiantes

   En las dos soluciones anteriores, la recursión empieza en la primera casa; se podría resolver análogamente empezando en la última casa, como ilustran las dos soluciones del ejercicio 2.

6. 0/1 knapsack - mochila 0/1

   Clase de teoría TE1 28/11 - 05/12

   En un centro comercial nos ha tocado un premio que consiste en que nos podemos llevar los objetos que queramos con la única restricción de que la suma de sus pesos no supere pesoMáximo. De cada uno de los n objetos que hay en el centro comercial, hay disponible una sola unidad, que es indivisible. Para i = 0, 1, ..., n - 1, el objeto i-ésimo tiene un peso peso[i] y un valor valor[i]. Tanto pesoMáximo como los pesos de los objetos son enteros positivos.

   Diseña, analiza sus costes e implementa un algoritmo eficiente para averiguar, a partir de los datos anteriores, cuál es la suma de valores máxima que podemos conseguir sin que la correspondiente suma de pesos supere pesoMáximo.

   Por ejemplo, con los siguientes datos:

   objeto	0	1	2	3
   peso	100	40	50	80
   valor	5000	3600	4500	8000

   y con pesoMáximo = 100, el resultado sería 8100, que corresponde a elegir los objetos 1 y 2, cuyo peso suma 90. Observa que no necesariamente nos interesa elegir el objeto de mayor peso, el de mayor valor, o el de mayor valor por unidad de peso.

   Si nos diesen los siguientes datos:

   objeto	0	1	2	3	4
   peso	5	2	1	6	7
   valor	1800	600	100	2200	2800

   y pesoMáximo = 15, el resultado sería 5600, que corresponde a elegir los objetos 1, 3 y 4, cuyo peso suma 15.

   Completa este código de prueba.

   Ayuda: solución recursiva inicial

   Solución

   Costes

   Este problema, al igual que el ejercicio 2 y la mayoría de los problemas anteriores, es simétrico y se podría resolver en la dirección contraria.

Nivel de dificultad 2 (con bucles, combinados con recursión, en la versión 1)

7. Clase de teoría TE1 05/12

   [Fuente: el problema b es el problema 8.32, en la página 315, del libro "Fundamentos de Algoritmia" (1997) de Gilles Brassard y Paul Bratley]

   En las orillas de un rio hay n ≥ 3 aldeas, numeradas de 0 a n - 1 en el sentido de la corriente. Para desplazarnos de una aldea a otra podemos alquilar una barca, con la que solamente podemos navegar rio abajo. Nuestro objetivo es llegar desde la primera aldea hasta la última con coste mínimo. Podemos hacer escalas en otras aldeas si nos interesa.

   En ese escenario, se plantean los siguientes dos problemas. El problema a te debería resultar sencillo, después de haber resuelto los ejercicios previos. Una vez resuelto el problema a, piensa qué es lo que cambia para resolver el b.

   1. Supongamos que, para seguir viaje desde la aldea i, tenemos a lo sumo dos opciones:

      • alquilar una barca que nos lleve desde la aldea i hasta la i + 1 con coste paseoCorto[i], o

      • alquilar una barca que nos lleve desde la aldea i hasta la i + 2 (si existe) con coste paseoLargo[i].

      1. Diseña, analiza sus costes e implementa un algoritmo eficiente que, a partir de los vectores paseoCorto y paseoLargo, calcule el mínimo coste de ir desde la primera aldea hasta la última.

         Completa este código de prueba.

         Ayuda: solución recursiva inicial

         Solución 1: recursión empieza en la última aldea

         Solución 2: recursión empieza en la primera aldea

         Costes

      2. Añade a cualquiera de las soluciones anteriores lo que creas conveniente para mostrar la secuencia de aldeas por las que se pasa en el viaje de mínimo coste, tanto en la versión 2 como en la versión 3.

         Solución

   2. Supongamos ahora que, para seguir viaje desde la aldea i, podemos alquilar una barca que nos lleve a cualquier aldea j > i con coste costeAlquiler[i][j] ≥ 0.

      Diseña, analiza sus costes e implementa un algoritmo eficiente que, a partir de la información de la matriz costeAlquiler, calcule el mínimo coste de ir desde la primera aldea hasta la última.

      Completa este código de prueba.

      Ayuda: solución recursiva inicial

      Solución 1: recursión empieza en la última aldea

      Solución2: recursión empieza en la primera aldea

      Aprende más ayudando a otros estudiantes

      Costes

8. Unbounded knapsack

   Clase de teoría TE1 05/12

   Para premiar nuestra fidelidad, una tienda online utiliza una estrategia de gamificación que nos permite, al superar retos, acumular puntos canjeables por regalos de un catálogo. Para i = 0, ..., n - 1, el artículo i-ésimo del catálogo tiene un precio valor[i] y lo podemos obtener gratis a cambio de puntos[i]. Los puntos son enteros positivos. De cada uno de los n artículos del catálogo, podemos canjear por puntos tantas unidades como queramos, con la única restricción de que la suma de puntos no supere nuestro saldoDePuntos. Cada uno de los artículos es indivisible.

   Necesitamos una función que, a partir de esos datos, calcule la suma de valores máxima de los artículos que podemos conseguir canjeando puntos por regalos.

   Diseña, analiza sus costes e implementa un algoritmo eficiente que resuelva ese problema.

   Por ejemplo, con saldoDePuntos = 15 y n = 5 artículos que tienen los siguientes puntos y valores:

   artículo	0	1	2	3	4
   puntos	12	8	5	3	15
   valor	400	350	180	100	500

   el resultado sería 100 + 100 + 350 = 550, correspondiente a canjear 14 puntos por dos unidades del artículo 3 (por 3 puntos cada una) y una unidad del artículo 1 (por 8 puntos).

   Completa este código de prueba.

   Solución

   Costes

9. Coin change

   Clase de prácticas LA2 y LA4 10/12, LA1 y LA3 12/12

   El tiempo estimado de resolución de este ejercicio, incluyendo la discusión inicial en clase, es de 1.5 horas.

   Los habitantes de un lejano país disponen de n tipos de monedas, cuyos valores son monedas[1], monedas[2], ..., monedas[n]. Dichos valores son enteros positivos. Tenemos que averiguar cuál es la mínima cantidad de monedas necesaria para sumar exactamente el valor deuda, suponiendo que disponemos de cantidad suficiente de monedas de todos los tipos. El objetivo siempre se puede conseguir, gracias a que existen monedas cuyo valor es 1.

   Por ejemplo:

   • Si monedas = {5, 21, 1, 25} y deuda = 63 entonces la solución sería 3, correspondiente a coger 3 monedas de valor 21 para sumar 63.

     Observa que ese resultado no es el que obtendría un algoritmo voraz que empiece devolviendo la máxima cantidad posible de la moneda más grande (en este ejemplo, dos monedas de 25), después de la siguiente, y así sucesivamente (así cogeríamos 2 monedas de 25, 2 de 5 y 3 de 1, en total 7 monedas). Ese algoritmo no resolvería correctamente el problema.

   • Con monedas = {5, 21, 1, 25} y deuda = 65 la solución sería 5, correspondiente a coger 2 monedas de valor 25 y 3 de valor 5 para sumar 65, o bien a coger 3 monedas de valor 21 y 2 de valor 1.

   • Con monedas = {1, 4, 6, 10} y deuda = 22 la solución sería 3, correspondiente a 22 = 10 + 6 + 6

     Observa que ese resultado es mejor que devolver 4 monedas sumando 22 = 10 + 10 + 1 + 1 o 22 = 6 + 6 + 6 + 4. La solución óptima no se construye con la máxima cantidad posible de monedas de 10 o la máxima cantidad posible de monedas de 6 o la máxima cantidad posible de monedas de 4 o la máxima cantidad posible de monedas de 1.

   1. Diseña, analiza sus costes e implementa un algoritmo eficiente que, dados deuda y el vector monedas, calcule la mínima cantidad de monedas que suman deuda.

   2. Modifica la implementación para que muestre en la salida estándar las monedas correspondientes a la solución del apartado anterior (en caso de empate entre varias soluciones, mostrará una cualquiera de ellas).

   Completa este código de prueba. Cuando veas que la versión 1 tarda mucho en obtener el quinto resultado, puedes interrumpirla y repetir la prueba con la versión 2.

   Ayuda: solución recursiva inicial

   Antes de ver la siguiente solución, revisa esta recopilación de errores frecuentes en implementaciones de Programación Dinámica.

   Solución (compara de nuevo la versión 1 con la 2 y la 2 con la 3 para ver cómo se ha pasado de una a otra con las transformaciones mínimas necesarias)

   Costes

10. Rod cutting

    Una fábrica de tuberías quiere calcular el máximo beneficio total que puede obtener con una tubería de longitud n, siendo n un valor entero. Puede venderla sin cortar, o cortarla y venderla por piezas cuya longitud sea un entero. Para i = 1, ..., n, el beneficio que se obtiene al vender una pieza de longitud i es beneficio[i].

    Necesitamos una función cuya entrada sea un vector beneficio de talla n + 1, y cuya salida sea el máximo beneficio total que se puede obtener con una tubería de longitud n.

    Diseña, analiza sus costes e implementa un algoritmo eficiente que resuelva ese problema.

    Por ejemplo, con n = 10 y estos datos:

    longitud	0	1	2	3	4	5	6	7	8	9	10
    beneficio	0	1	5	8	9	10	17	17	20	24	26

    el máxímo beneficio total que se puede obtener con una tubería de longitud 10 es 5 + 5 + 17 = 27, y se obtiene sumando los beneficios de vender tres piezas de longitudes 2, 2 y 6. Eso es mejor que venderla sin cortar con beneficio 26.

    Completa este código de prueba.

    Ayuda: solución recursiva inicial

    Solución 1

    Costes

11. El escenario de un juego está formado por una matriz rectangular de celdas de tamaño filas · columnas. Las filas están numeradas desde 0 (que es la fila superior) hasta filas - 1 (que es la fila inferior). Las columnas están numeradas desde 0 hasta columnas - 1. El jugador puede elegir cualquier celda de la fila inferior para empezar y debe terminar en cualquier celda de la fila superior. Para avanzar, en cada paso puede saltar desde la celda en la que está hasta cualquier celda de la fila situada inmediatamente encima de esa.

    Durante su recorrido, va consumiendo una cantidad de energía que depende tanto de las celdas por las que pasa como de los saltos que realiza:

    • Para cualquier celda (fila, columna), pasar por ella consume una cantidad de energía energíaCelda[fila][columna].

    • La energía que consume cada salto depende de entre qué columnas se salta, sin importar en qué fila sucede. Saltar de la celda (fila, columnaA) a la celda (fila - 1, columnaB) consume una cantidad de energía energíaSalto[columnaA][columnaB].

    Diseña, analiza sus costes e implementa un algoritmo eficiente que calcule, a partir de esos datos, la mínima cantidad de energía total que hace falta para superar el reto.

    Por ejemplo, con la siguiente matriz energíaCelda:

    		0	1	2	3
    	0	30	40	90	80
    	1	20	20	10	30
    	2	70	50	90	70
    	3	60	30	10	20
    	4	50	90	30	60
    	5	40	60	50	90

    y con la siguiente matriz energíaSalto:

    		0	1	2	3
    	0	0	35	85	25
    	1	5	0	45	15
    	2	65	75	0	25
    	3	95	25	15	0

    el resultado sería 255, correspondiente a elegir las siguientes celdas sombreadas:

    		0	1	2	3
    	0	30	40	90	80
    	1	20	20	10	30
    	2	70	50	90	70
    	3	60	30	10	20
    	4	50	90	30	60
    	5	40	60	50	90

    En ese recorrido, la energía consumida pasando por las celdas es 50 + 30 + 20 + 50 + 20 + 30 = 200 y la energía consumida saltando entre celdas es 0 + 25 + 25 + 5 + 0 = 55.

    Completa este código de prueba.

    Solución 1

    Solución 2

    Costes

12. Un deportista debe superar un reto al día durante n días consecutivos, siendo n > 1. Cada día puede elegir entre k tipos de retos disponibles. Cuando supera un reto de tipo j tras haber superado uno de tipo i el día anterior, consigue una cantidad de puntos no negativa puntos[i][j], para i = 0, ..., k - 1 y para j = 0, ..., k - 1. Se permite elegir el mismo tipo de reto varias veces, consecutivas o no. El primer reto superado no da puntos pero permite empezar a acumular puntos a partir del día siguiente.

    Diseña, analiza sus costes e implementa un algoritmo eficiente que calcule, a partir de esos datos, la máxima cantidad de puntos que puede acumular el deportista.

    Por ejemplo, con n = 4 días, k = 5 tipos de retos disponibles, y esta matriz puntos:

    		nadar	correr	flexiones	pesas	saltar
    		0	1	2	3	4
    nadar	0	60	70	120	610	50
    correr	1	210	300	170	600	100
    flexiones	2	150	450	100	500	40
    pesas	3	110	0	30	10	20
    saltar	4	620	320	90	240	80

    el resultado es 1350 y se obtiene superando, en este orden, retos de tipo 2, 1, 1 y 3, de modo que se acumulan puntos[2][1] + puntos[1][1] + puntos[1][3] = 450 + 300 + 600 puntos.

    Completa este código de prueba.

    Solución

    Costes

Nivel de dificultad 3

Los siguientes ejercicios son opcionales y no van para examen. Son propios de asignaturas que tienen más créditos para este tema. En ellos la dificultad del problema es mayor y, por ello, no se pretende que seas capaz de encontrar la solución recursiva inicial. El objetivo es que, una vez entendida consultando la bibliografía, seas capaz de programarla eficientemente aplicando lo que has aprendido hasta ahora.

13. Ejercicio opcional

    Longest common subsequence (LCS)

    Sean dos secuencias A = A₁A₂...A_n y B = B₁B₂...B_m, formadas por elementos de un alfabeto finito dispuestos en un determinado orden. Una subsecuencia es el resultado de eliminar cero o más elementos de una secuencia, manteniendo el orden de los elementos restantes.

    Necesitamos un algoritmo eficiente para, dadas dos secuencias cualesquiera A y B, calcular la longitud de la subsecuencia común de A y B más larga posible.

    Por ejemplo, dadas A = barcelona y B = valencia:

    • ael es subsecuencia de A pero no es subsecuencia de B.

    • alena es subsecuencia de B pero no es subsecuencia de A.

    • Una subsecuencia común de A y B es aea, de longitud 3.

    • Otras subsecuencias comunes de A y B, más largas que aea, son aena y alna, de longitud 4.

    • Como no hay subsecuencias comunes más largas que esas, el resultado buscado sería 4.

    Puedes encontrar una solución recursiva para ese problema en estos apartados de la Wikipedia:

    • Longest common subsequence problem: Solution for two sequences

    • Problema de Subsecuencia Común mas Larga: Solución para dos secuencias

    Tras entender esa solución recursiva, como ejercicio (a) escribe un algoritmo recursivo que resuelva el problema eficientemente empleando Programación Dinámica, (b) después conviértelo en un algoritmo que calcule lo mismo de forma no recursiva, y (c) analiza el coste temporal y espacial de ambos.

    Solución (pseudocódigo)

14. Ejercicio opcional

    Sequence alignment

    Para ver otro ejemplo importante de aplicación de la Programación Dinámica, lee el apartado 3.7 "Sequence Alignment" del libro "Foundations of Algorithms" (2015) de R. E. Neapolitan.

    Tras entender las explicaciones, como ejercicio (a) escribe un algoritmo recursivo que resuelva el problema eficientemente empleando Programación Dinámica, (b) después conviértelo en un algoritmo que calcule lo mismo de forma no recursiva, y (c) analiza el coste temporal y espacial de ambos.

    Solución (pseudocódigo)

15. Ejercicio opcional

    Chained matrix multiplication

    El apartado 3.4 "Chained Matrix Multiplication" del libro "Foundations of Algorithms" (2015) de R. E. Neapolitan explica otro ejemplo importante de aplicación de la Programación Dinámica.

    Alternativamente, puedes encontrar una descripción diferente del mismo tema en el apartado 10.3.2 "Ordering Matrix Multiplications" del capítulo 10 "Algorithm Design Techniques" del libro "Data Structures and Algorithm Analysis in C++" (2014) de M. A. Weiss.

    En castellano puedes encontrar lo mismo (excepto el código C++) en el capítulo 10 "Técnicas de diseño de algoritmos" del libro "Estructuras de datos y algoritmos" (1995) de M. A. Weiss.