Algoritmos y Estructuras de Datos (VJ1215)

Habiendo resuelto previamente el ejercicio 9.d, basta comprobar que están ordenados de menor a mayor los datos del vector en el que hemos puesto a la izquierda de cada dato lo que hay en su subárbol izquierdo y a la derecha de cada dato lo que hay en su subárbol derecho.

void Conjunto::obtenerOrdenados(Nodo * n, vector<int> & v, int & i) const {
   if (n != nullptr) {
      obtenerOrdenados(n->izquierdo, v, i);
      v[i++] = n->dato;
      obtenerOrdenados(n->derecho, v, i);
   }
}

bool Conjunto::esArbolBinarioDeBusqueda() const {
   vector<int> v(laTalla);
   int i = 0;
   obtenerOrdenados(raiz, v, i);
   for (i = 1; i < v.size(); i++)
      if (v[i] < v[i - 1])
	 return false;
   return true;
}
	

El coste temporal de esta solución es el mismo que el de la solución del ejercicio 9.d: O(n), siendo n la talla del conjunto.

Si nos queremos ahorrar el vector en la solución anterior, podemos hacer lo siguiente:

#include <limits>

bool Conjunto::esArbolBinarioDeBusqueda(Nodo * n, int & mayorHastaAhora) const {
   if (n == nullptr)
      return true;
   if (! esArbolBinarioDeBusqueda(n->izquierdo, mayorHastaAhora))
      return false;
   if (n->dato < mayorHastaAhora)
      return false;
   mayorHastaAhora = n->dato;
   return esArbolBinarioDeBusqueda(n->derecho, mayorHastaAhora);
}   

bool Conjunto::esArbolBinarioDeBusqueda() const {
   int mayorHastaAhora = numeric_limits<int>::min();
   return esArbolBinarioDeBusqueda(raiz, mayorHastaAhora);
}
	

En esta solución se ha hecho uso de numeric_limits<int>::min(), que es el mínimo valor posible de tipo int.

El coste temporal de esta solución sigue siendo O(n).

Para resolver el problema recursivamente, podemos comprobar que en cada nodo su subárbol izquierdo es válido, su subárbol derecho es válido, y el dato del propio nodo es válido.

Por ejemplo, en el siguiente árbol, todos los datos del subárbol derecho del 20 han de ser mayores o iguales que 20 y menores o iguales que 50. Una vez comprobado que el 48 lo cumple, podemos seguir comprobando que los datos del subárbol izquierdo del 48 están entre 20 y 48 y que los datos del subárbol derecho del 48 están entre 48 y 50.

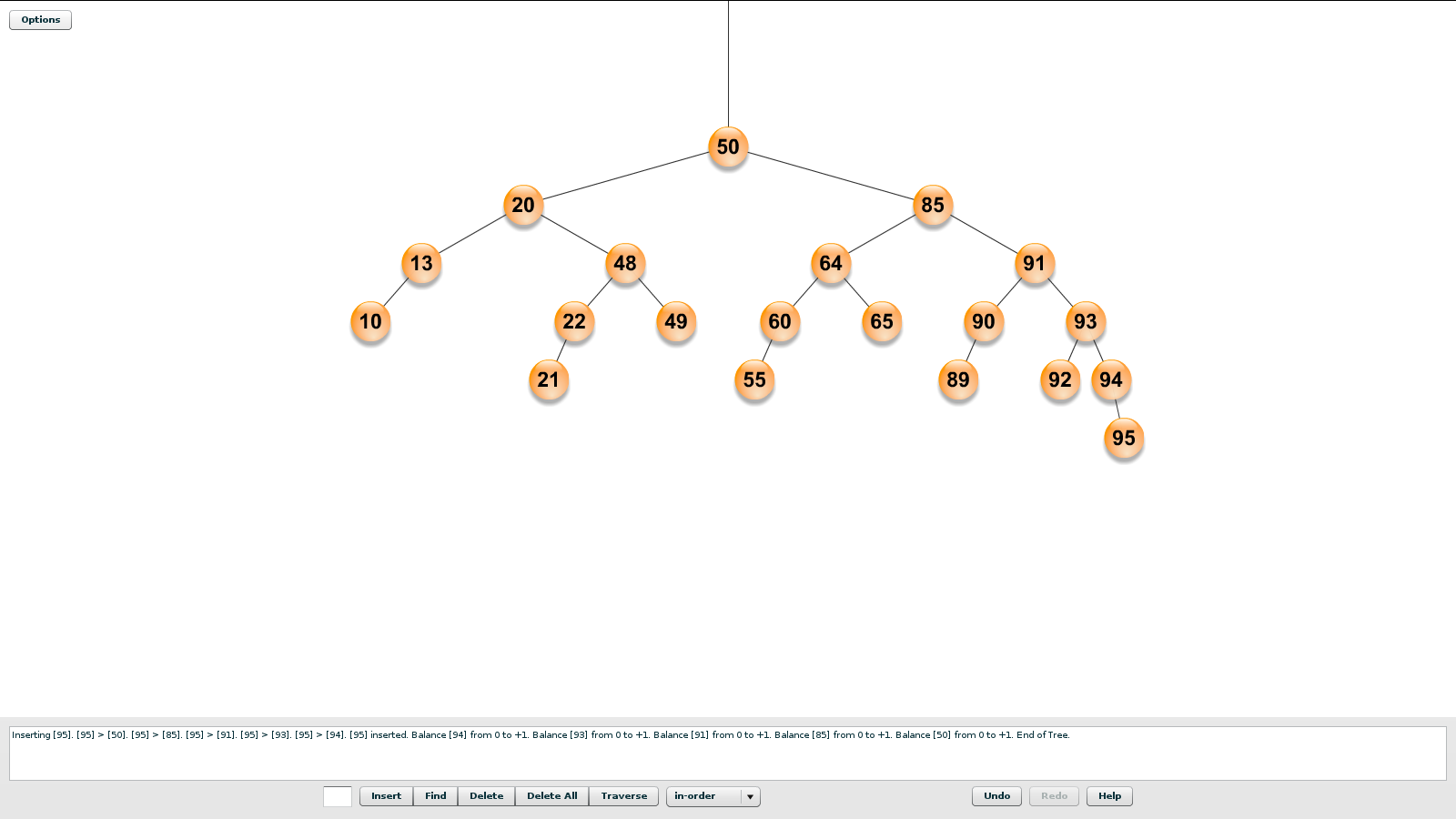
Para ello, pasamos a cada llamada recursiva los dos límites entre los que deben estar los datos del subárbol, y vamos actualizando dichos límites. Podemos utilizar numeric_limits<int>::max() para empezar con el máximo valor posible de tipo int como límite superior, y análogamente numeric_limits<int>::min() para empezar con el mínimo valor posible de tipo int como límite inferior.

#include <limits>

bool Conjunto::esArbolBinarioDeBusqueda() const {
   int maximoInt = numeric_limits<int>::max();
   int minimoInt = numeric_limits<int>::min();
   return raiz == nullptr || datosEstanEntreLimites(raiz, minimoInt, maximoInt);
}

bool Conjunto::datosEstanEntreLimites(Nodo * n, int limiteInferior, int limiteSuperior) const {
   return n->dato >= limiteInferior
          && n->dato <= limiteSuperior
          && (n->izquierdo == nullptr || datosEstanEntreLimites(n->izquierdo, limiteInferior, n->dato))
          && (n->derecho == nullptr || datosEstanEntreLimites(n->derecho, n->dato, limiteSuperior));
}
	

Por supuesto, contamos con que los operadores booleanos se evalúan en cortocircuito. Alternativamente, si lo prefieres:

bool Conjunto::datosEstanEntreLimites(Nodo * n, int limiteInferior, int limiteSuperior) const {
   if (n->dato < limiteInferior)
      return false;
   if (n->dato > limiteSuperior)
      return false;
   if (n->izquierdo != nullptr && ! datosEstanEntreLimites(n->izquierdo, limiteInferior, n->dato))
      return false;
   if (n->derecho != nullptr && ! datosEstanEntreLimites(n->derecho, n->dato, limiteSuperior))
      return false;
   return true;
}
	

El coste propio de cada llamada a datosEstanEntreLimites es O(1), y en el peor caso se hace una llamada por nodo. Por tanto, el coste temporal de esta solución es O(n), siendo n la talla del conjunto, que coincide con la cantidad de nodos del árbol. No puede haber una solución más eficiente si tenemos que verificar que los n datos del árbol están correctamente situados: si dejamos de consultar alguno de ellos, ese puede ser incorrecto.

En la solución hemos utilizado el mínimo y máximo valor entero representable para inicializar los límites inferior y superior. Alternativamente, podríamos haber usado los valores mínimo y máximo que contenga el árbol en ese momento. Si no los tenemos precalculados, o si los valores precalculados tampoco son fiables, podemos buscar el mínimo y el máximo en tiempo O(n) recorriendo todo el árbol (al no saber si es un árbol binario de búsqueda, no valdría buscar el mínimo yendo siempre hacia la izquierda ni buscar el máximo yendo siempre hacia la derecha). En cualquier caso, el coste total seguiría siendo O(n).

Una solución equivalente es la siguiente:

#include <limits>

bool Conjunto::esArbolBinarioDeBusqueda() const {
   int maximoInt = numeric_limits<int>::max();
   int minimoInt = numeric_limits<int>::min();
   return datosEstanEntreLimites(raiz, minimoInt, maximoInt);
}

bool Conjunto::datosEstanEntreLimites(Nodo * n, int limiteInferior, int limiteSuperior) const {
   return n == nullptr
          || (n->dato >= limiteInferior
              && n->dato <= limiteSuperior
              && datosEstanEntreLimites(n->izquierdo, limiteInferior, n->dato)
              && datosEstanEntreLimites(n->derecho, n->dato, limiteSuperior));
}
	

Esta versión no hace exactamente n llamadas recursivas porque hace también llamadas con argumento nulo, pero en cada nodo se lanzan a lo sumo dos llamadas y por tanto el coste en el peor caso sigue siendo O(n).