Regresión Logística

Introducción

Aunque hablemos de regresión logística, realmente utilizamos este modelo para tareas de clasificación.

Empezaremos mostrando cómo aplicar la regresión logística cuando sólo tenemos dos clases, y queremos clasificar nuevas instancias como pertenecientes a alguna de las dos clases.

Después extenderemos el concepto para tareas de clasificación de más de dos clases.

Objetivos de aprendizaje

Resumir en qué consiste la regresión logística.
Interpretar los resultados de los análisis de distribuciones y covarianzas de los datos.
Decidir si un problema de clasificación se puede abordar con regresión logística.
Construir un algoritmo de clasificación a partir de la regresión logística.

Referencias

Hands-on Machine Learning. Capítulo 4.
Pattern recognition and Machine Learning. Capítulo 4.

Algunos conceptos previos

Teorema de Bayes

El teorema de Bayes es uno de los más importantes de la teoría de la probabilidad. Nos permite calcular la probabilidad de un suceso a partir de otras probabilidades relacionadas con el suceso.

La probabilidad de que ocurran dos sucesos A y B se calcula como:

\[ p(A,B) = p(A) p(B|A) \]

Donde \(p(B|A)\) significa la probabilidad de B condicionada a que se haya producido A. Fíjate en que si A y B son independientes \(p(B|A) = p(B)\) y por lo tanto \(p(A,B) = p(A) p(B)\).

Teorema de Bayes

Como los sucesos son intercambiables también podemos escribir:

\[ p(B,A) = p(B) p(A|B) \]

Igualando ambas expresiones:

\[ p(A) p(B|A) = p(B) p(A|B) \]

Y despejando \(p(A|B)\)

\[ p(A|B) = \frac{p(A) p(B|A)}{p(B)} \]

Teorema de Bayes

La expresión anterior es el teorema de Bayes:

\[ p(A|B) = \frac{p(A) p(B|A)}{p(B)} \]

Veamos un ejemplo para aclarar su significado.

Teorema de Bayes

Supongamos que una persona se hace una prueba de covid-19 y le da positivo, ¿cuál es la probabilidad de que la persona tenga covid-19?

Si escribimos esta pregunta en forma de probabilidades \(p(covid|positiva)\) y aplicando el teorema de Bayes:

\[ p(covid|positiva) = \frac{p(covid) p(positiva|covid)}{p(positiva)} \]

Donde: \[p(positiva) = p(positiva|covid) p(covid) + \\ p(positiva|!covid) p(!covid)\]

Teorema de Bayes

Supongamos que la matriz de confusión que el laboratorio publica sobre los resultados de las pruebas son los siguientes:

		Prueba	Prueba
		positiva	negativa
Real	positiva	4950	50
Real	negativa	100	4900

Además, la prevalencia de la covid es de 1 persona entre 1.000.

Teorema de Bayes

Calculando todas las cantidades:

\(p(positiva|covid) = 4950/5000 = 0.99\)

\(p(covid) = 0.001\)

\(p(positiva|!covid) = 100/5000 = 0.02\)

\(p(covid) = 0.001\)

\(p(!covid) = 0.999\)

\(p(positiva) = p(positiva|covid) p(covid) + \\p(positiva|!covid) p(!covid)\)

\(p(positiva) = 0.99 \cdot 0.001 + 0.02 \cdot 0.999 = 0.20079\)

Teorema de Bayes

Sustituyendo finalmente en la fórmula del teorema de Bayes:

\[ p(covid|positiva) = \frac{p(covid) p(positiva|covid)}{p(positiva)} = \\ \frac{0.99 \cdot 0.001}{0.20079} = 0.00493 \]

Que se interpreta como: si tomamos una persona al azar, le hacemos la prueba de covid-19 y da positivo, la probabilidad de que realmente tenga la enfermedad es del 0.5%.

Definir del problema

Género a partir de peso y altura

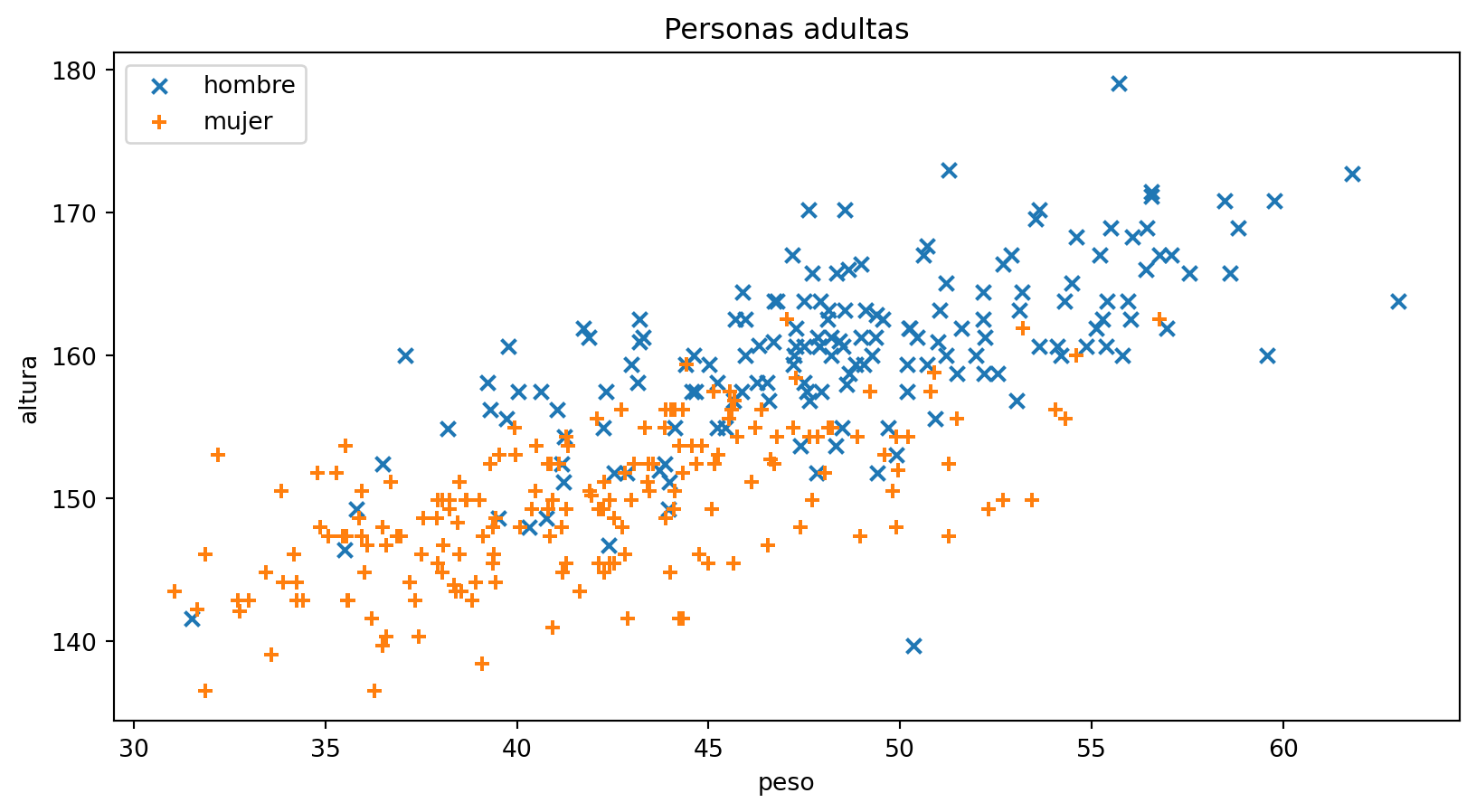
Volvamos al conjunto de datos de Howell

Show me the code

Para generar la figura con todos los datos

url = "https://raw.githubusercontent.com/rmcelreath/rethinking/master/data/Howell1.csv"
data = pd.read_csv(url, sep=";")
hombres = data[data["male"] == 1]
mujeres = data[data["male"] == 0]
colors = {1: "tab:red", 0: "tab:blue"}
plt.scatter(hombres["weight"], hombres["height"], marker="x")
plt.scatter(mujeres["weight"], mujeres["height"], marker="+")
plt.title("Todas las personas del conjunto")
plt.legend(["hombre", "mujer"], loc="upper left")
plt.xlabel("peso")
plt.ylabel("altura");

Show me the code

Para generar la figura con personas adultas:

adultos = data[data["age"] >= 18]
hombres_adultos = adultos[adultos["male"] == 1]
mujeres_adultas = adultos[adultos["male"] == 0]
plt.scatter(hombres_adultos["weight"], hombres_adultos["height"], marker="x")
plt.scatter(mujeres_adultas["weight"], mujeres_adultas["height"], marker="+")
plt.title("Personas adultas")
plt.legend(["hombre", "mujer"], loc="upper left")
plt.xlabel("peso")
plt.ylabel("altura");

Género a partir de peso y altura

Parece que, a partir de la edad adulta (18 años), existen diferencias entre hombres y mujeres si atendemos al peso y la altura, ojo!!! para el conjunto de datos que estamos utilizando.

Ahora, vamos a intentar construir un clasificador que nos permita realizar esa clasificación.

Obtener los datos

Conjunto de datos Howell

Los datos ya los tenemos, son los del conjunto de datos de Howell.

Afortunadamente, los datos están limpios, es decir, todas las muestras contienen valores para todas las características, no hay datos duplicados, etcétera.

De nuevo, las conclusiones que extraigamos son válidas únicamente para ese conjunto de datos.

Explorar los datos

Antes de intentar utilizar algún algoritmo, es muy recomendable estudiar los datos desde el punto de vista estadístico, por ejemplo:

¿Los datos tienen alguna distribución conocida?
¿Existen correlaciones entre los datos?

Distribuciones de los datos

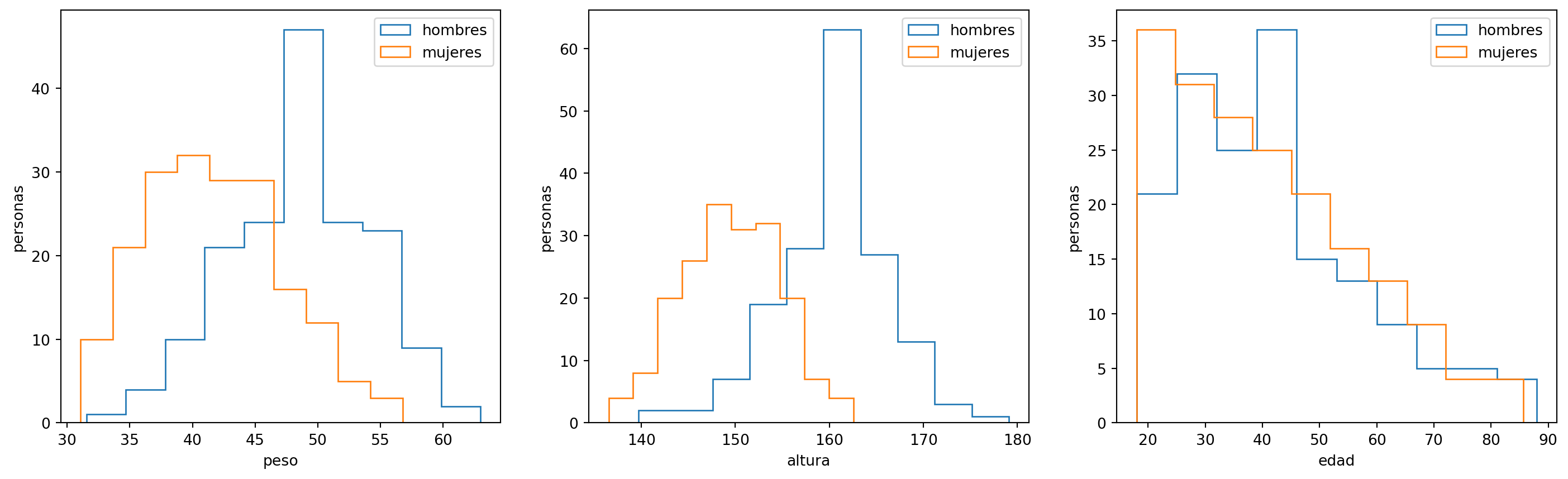
Quizás, las distribuciones de peso y altura sigan una distribución normal, es lo que sabemos de datos poblacionales generales.

Show me the code

Para generar los histogramas

f, (ax1, ax2, ax3) = plt.subplots(1, 3)
f.set_figwidth(18)
ax1.hist(hombres_adultos.weight, histtype="step")
ax1.set_xlabel("peso"); ax1.set_ylabel("personas")
ax1.hist(mujeres_adultas.weight, histtype="step")
ax1.legend(["hombres", "mujeres"])
ax2.hist(hombres_adultos.height, histtype="step")
ax2.set_xlabel("altura"); ax2.set_ylabel("personas")
ax2.hist(mujeres_adultas.height, histtype="step")
ax2.legend(["hombres", "mujeres"])
ax3.hist(hombres_adultos.age, histtype="step")
ax3.hist(mujeres_adultas.age, histtype="step")
ax3.set_xlabel("edad"); ax3.set_ylabel("personas")
ax3.legend(["hombres", "mujeres"])
plt.show()

Distribuciones de los datos

Hagamos un ajuste:

p-valor ajuste peso hombres adultos:  0.6793035002887847
p-valor ajuste peso mujeres adultas:  0.5783230557872278
p-valor ajuste altura hombres adultos:  0.17252103247585238
p-valor ajuste altura mujeres adultas:  0.6661348374682965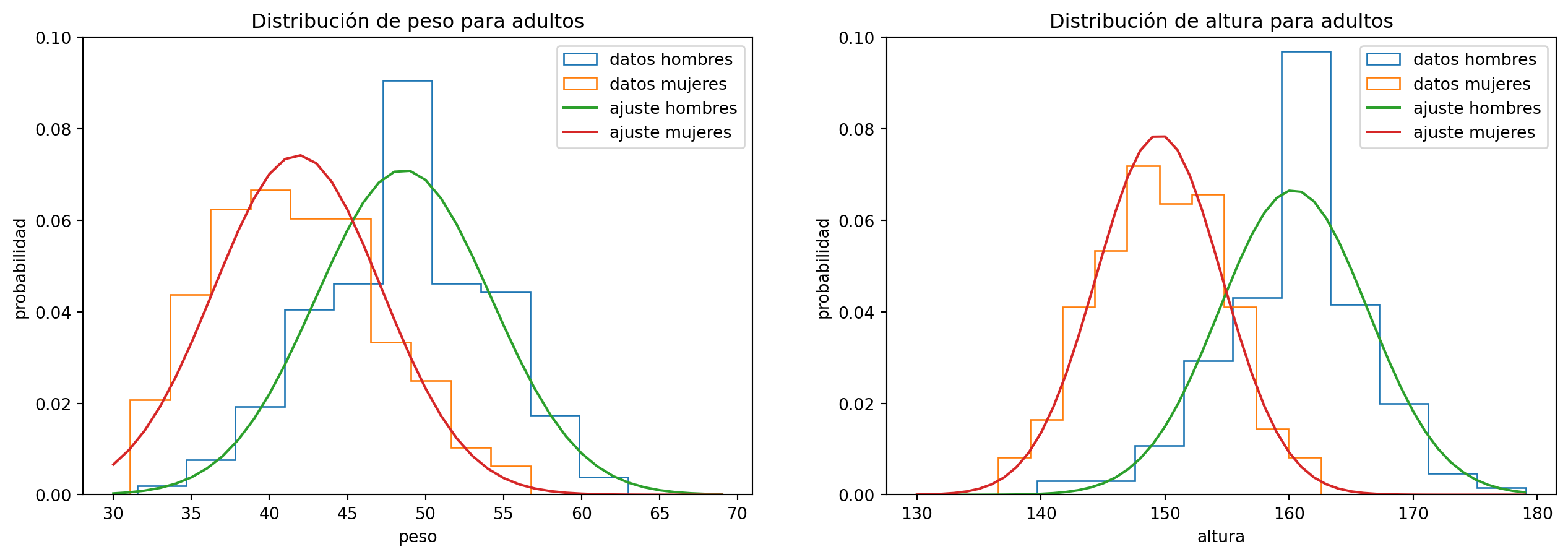

Show me the code

Para hacer el ajuste a una distribución normal:

mu, std = np.mean(hombres_adultos["weight"]), np.std(hombres_adultos["weight"])
pdf_peso_hombres = stats.norm(mu, std)
cdf = pdf_peso_hombres.cdf
test = stats.ks_1samp(hombres_adultos["weight"], cdf)
print("p-valor ajuste peso hombres adultos: ", test.pvalue)
mu, std = np.mean(mujeres_adultas["weight"]), np.std(mujeres_adultas["weight"])
pdf_peso_mujeres = stats.norm(mu, std)
cdf = pdf_peso_mujeres.cdf
test = stats.ks_1samp(mujeres_adultas["weight"], cdf)
print("p-valor ajuste peso mujeres adultas: ", test.pvalue)

mu, std = np.mean(hombres_adultos["height"]), np.std(hombres_adultos["height"])
pdf_altura_hombres = stats.norm(mu, std)
cdf = pdf_altura_hombres.cdf
test = stats.ks_1samp(hombres_adultos["height"], cdf)
print("p-valor ajuste altura hombres adultos: ", test.pvalue)
mu, std = np.mean(mujeres_adultas["height"]), np.std(mujeres_adultas["height"])
pdf_altura_mujeres = stats.norm(mu, std)
cdf = pdf_altura_mujeres.cdf
test = stats.ks_1samp(mujeres_adultas["height"], cdf)
print("p-valor ajuste altura mujeres adultas: ", test.pvalue)

f, (ax1, ax2) = plt.subplots(1, 2)
f.set_figwidth(16)
ax1.hist(hombres_adultos["weight"], histtype="step", density=True, bins=10, label="datos hombres")
ax1.hist(mujeres_adultas["weight"], histtype="step", density=True, bins=10, label="datos mujeres")
rango = range(30, 70)
pdf = [pdf_peso_hombres.pdf(x) for x in rango]
ax1.plot(rango, pdf, label="ajuste hombres")
ax1.set_ylim(0, 0.1)
ax1.set_title("Distribución de peso para adultos")
ax1.set_xlabel("peso")
ax1.set_ylabel("probabilidad")
pdf = [pdf_peso_mujeres.pdf(x) for x in rango]
ax1.set_ylim(0, 0.1)
ax1.plot(rango, pdf, label="ajuste mujeres")
ax1.set_xlabel("peso")
ax1.set_ylabel("probabilidad")
ax1.legend()

ax2.hist(hombres_adultos["height"], histtype="step", density=True, bins=10, label="datos hombres")
ax2.hist(mujeres_adultas["height"], histtype="step", density=True, bins=10, label="datos mujeres")
rango = range(130, 180)
pdf = [pdf_altura_hombres.pdf(x) for x in rango]
ax2.plot(rango, pdf, label="ajuste hombres")
ax2.set_ylim(0, 0.1)
ax2.set_title("Distribución de altura para adultos")
ax2.set_xlabel("altura")
ax2.set_ylabel("probabilidad")
pdf = [pdf_altura_mujeres.pdf(x) for x in rango]
ax2.set_ylim(0, 0.1)
ax2.plot(rango, pdf, label="ajuste mujeres")
ax2.set_xlabel("altura")
ax2.set_ylabel("probabilidad")
ax2.legend()

Distribuciones de los datos

Es importante la bondad del ajuste. En este caso, todos los p-valores están por encima de 0.05, luego podemos considerar que los datos de peso y altura siguen distribuciones normales tanto para hombres como para mujeres.

Correlaciones en los datos

Vamos a explorar las correlaciones entre los datos. Empezamos con los adultos:

	height	weight	age	male
height	1.000000	0.754748	-0.101838	0.699993
weight	0.754748	1.000000	-0.172904	0.524453
age	-0.101838	-0.172904	1.000000	0.028455
male	0.699993	0.524453	0.028455	1.000000

adultos.corr()

Correlaciones en los datos

Si analizamos los datos por género, y dejamos fuera la edad.

Hombres

	height	weight	age
height	1.000000	0.655591	-0.156606
weight	0.655591	1.000000	-0.209690
age	-0.156606	-0.209690	1.000000

Mujeres

	height	weight	age
height	1.000000	0.620260	-0.186342
weight	0.620260	1.000000	-0.230822
age	-0.186342	-0.230822	1.000000

Las correlaciones entre peso y altura son parecidas entre hombres y mujeres.

hombres_adultos.drop(columns=["male"]).corr()
mujeres_adultas.drop(columns=["male"]).corr()

Covarianza en los datos

Otro dato que nos sera de utilidad más tarde, y relacionado con el anterior, es la covarianza de los datos:

Hombres

	height	weight	age
height	36.110209	22.201674	-14.786658
weight	22.201674	31.759585	-18.567886
age	-14.786658	-18.567886	246.884306

Mujeres

	height	weight	age
height	25.852920	16.992186	-15.367846
weight	16.992186	29.029653	-20.171912
age	-15.367846	-20.171912	263.085063

Las covarianzas (peso y altura) tienen cierto parecido entre hombres y mujeres en este conjunto de datos.

hombres_adultos.drop(columns=["male"]).cov()
mujeres_adultas.drop(columns=["male"]).cov()

Normalidad multivariada

Por último, comprobemos si las distribución de los datos, cuando sólo tenemos en cuenta el peso y la altura de las personas, y separamos por género, siguen una distribución normal.

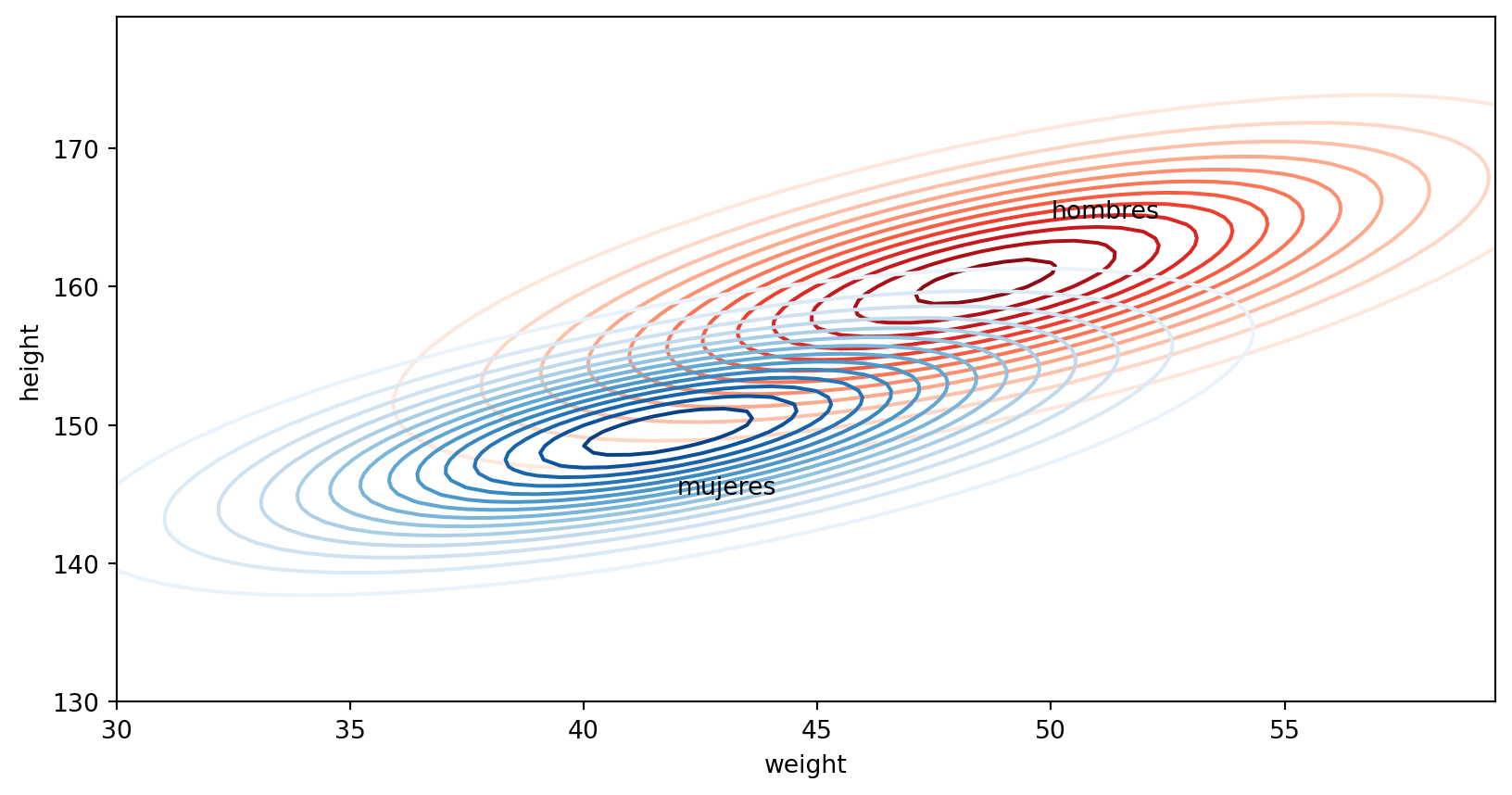
Show me the code

columns = ["weight", "height"]
medias_hombres = hombres_adultos[columns].mean()
medias_mujeres = mujeres_adultas[columns].mean()
covarianza_hombres = hombres_adultos[columns].cov()
covarianza_mujeres = mujeres_adultas[columns].cov()
x, y = np.mgrid[30:60:0.5, 130:180:0.5]
pos = np.dstack((x,y))
normal_hombres = stats.multivariate_normal(medias_hombres, covarianza_hombres)
plt.contour(x, y, normal_hombres.pdf(pos), levels=14, cmap="Reds")

normal_mujeres = stats.multivariate_normal(medias_mujeres, covarianza_mujeres)
plt.contour(x, y, normal_mujeres.pdf(pos), levels=14, cmap="Blues")
plt.xlabel("weight")
plt.ylabel("height")
plt.annotate("hombres", (50, 165))
plt.annotate("mujeres", (42,145));

Normalidad multivariada

Para ajustar los datos a una normal multivariada:

import pingouin as pg
from scipy import stats

ajuste_hombres = stats.multivariate_normal.fit(hombres_adultos[columns])
test_hombres = pg.multivariate_normality(hombres_adultos[columns])
ajuste_mujeres = stats.multivariate_normal.fit(mujeres_adultas[columns])
test_mujeres = pg.multivariate_normality(mujeres_adultas[columns])

El dato importante es la bondad del ajuste que obtenemos con multivariate_normality:

Bondad del ajuste para hombres:  HZResults(hz=0.7326666288692368, pval=0.25984280317567643, normal=True)
Bondad del ajuste para mujeres:  HZResults(hz=0.9710743539320273, pval=0.07232144985695443, normal=True)

Normalidad multivariada

En ambos casos el p-valor del ajuste está por encima de 0.05 que se considera el estándar para asegurar que la hipótesis es correcta.

p-valor ajuste hombres:  0.25984280317567643
p-valor ajuste mujeres:  0.07232144985695443

print("p-valor ajuste hombres: ", test_hombres.pval)
print("p-valor ajuste mujeres: ", test_mujeres.pval)

Conclusiones

Las conclusiones que podemos extraer son:

Existe una correlación alta entre altura y género.
Existe una correlación moderada entre peso y género.
No hay correlación entre edad y género.
Las correlaciones entre peso y altura son parecidas entre hombres y mujeres.
La matriz de covarianza (peso y altura) es parecida entre hombres y mujeres.
La distribución peso-altura sigue una normal para hombres y mujeres.

Preparar los datos

Afortunadamente, esta base de datos ya está preparada.

La preparación de los datos es una tarea muy costosa en tiempo. La limpieza de los datos implica, por ejemplo:

Eliminar datos duplicados.
Eliminar datos que son erróneos.
Decidir qué hacer con los datos de los que falta alguna característica:
1. Eliminarlos.
2. Imputar un valor a la característica ausente.

El algoritmo de regresión logística para tareas de clasificación

Clasificación con dos clases

El problema de clasificar una persona de la base de datos Howell por género es un problema con dos únicas clases. Para generalizar, vamos a llamar a estas clases \(C_1\) y \(C_2\).

Utilizamos el teorema de Bayes para calcular la probabilidad de que una muestra \(x\) pertenezca a la clase \(C_1\):

\[ p(C_1|x) = \frac{p(C_1)p(x|C_1)}{p(C_1)p(x|C_1) + p(C_2)p(x|C_2)} \]

Clasificación con dos clases

Dividiendo numerador y denominador por el numerador:

\[ p(C_1|x) = \frac{1}{1 + \frac{p(C_2)p(x|C_2)}{p(C_1)p(x|C_1)}} = \frac{1}{1 + e^{-a}} = \sigma(a) \]

donde \(\sigma(a)\) es la función sigmoide con:

\[ a = ln \frac{p(C_1)p(x|C_1)}{p(C_2)p(x|C_2)} \]

Clasificación con dos clases

Y este es el aspecto de la función sigmoide:

Clasificación con dos clases

De momento, todo esto parece un poco artificial, pero va a ir tomando sentido.

Ahora supongamos que:

Las distribuciones de las variables en las clases \(C_1\) y \(C_2\) son gaussianas.
Las correlaciones de las variables son iguales en las dos clases.

Fíjate en que estas suposiciones son «validas» para los datos de Howell. Es importante comprobar que nuestros datos cumplen estas dos condiciones si vamos a aplicar la formulación siguiente.

Clasificación con dos clases

La distribución gaussiana en D dimensiones es:

\[ p(x|C_k) = \frac{1}{(2\pi)^{D/2}} \frac{1}{\lvert \Sigma \rvert^{1/2}} exp \Bigl \{ - \frac{1}{2} (x-\mu_k)^T \Sigma^{-1} (x-\mu_k) \Bigr \} \]

Donde \(k\) es 1 ó 2 para indicar la clase, \(\mu_k\) es la media de la clase \(k\), y \(\Sigma\) la matriz de covarianza.

Clasificación con dos clases

Si particularizamos para \(k=1\) y \(k=2\) y sustituimos en las formulas de la sigmoide obtenemos:

\[ p(C_1|x) = \sigma(\theta^T x + \theta_0) = \sigma(\theta^T x) \]

Esto significa que si hacemos una transformación lineal sobre una muestra \(\theta^T x\) y sobre el resultado aplicamos la función \(\sigma(\theta^T x)\) obtenemos la probabilidad de que la muestra \(x\).

Nos queda por calcular los parámetros de la transformación.

Clasificación con dos clases

Los parámetros son:

\[ \theta= \Sigma^{-1}(\mu_1 - \mu_2); \: \theta_0= -\frac{1}{2} \mu_1^T \Sigma^{-1} \mu_1 + \frac{1}{2} \mu_1^T \Sigma^{-1} \mu_1 + ln \frac{p(C_1)}{p(C_2)} \]

Donde los parámetros \(\mu_1\), \(\mu_2\) y \(\Sigma\) los podemos obtener aplicando el principio de máxima verosimilitud al conjunto de nuestros datos.

Clasificación con dos clases

Si tomamos \(p(C_1) = q\), y por lo tanto \(p(C_2) = 1-q\) y definimos \(t_n = 1\) si la muestra pertenece a la clase \(C_1\) y \(t_n = 0\) si la muestra pertenece a la clase \(C_2\) y hacemos uso de la definición de probabilidad:

\[ p(x_n, C_1) = p(C_1) p(x_n|C_1) = q N(x_n|\mu_1 \Sigma) \\ p(x_n, C_2) = p(C_2) p(x_n|C_2) = (1-q) N(x_n|\mu_2 \Sigma) \]

Y aplicamos el principio de máxima verosimilitud a nuestro conjunto de datos:

\[ p(\pmb{t}|q, \mu_1, \mu_2, \Sigma) = \prod_{n=1}^N [q N(x_n|\mu_1, \Sigma)]^{t_n} [(1-q) N(x_n|\mu_2, \Sigma)]^{(1-t_n)} \]

Clasificación con dos clases

Si tomamos la derivada de la anterior expresión con respecto a \(q\) e igualamos a cero:

\[ q = \frac{1}{N} \sum_{n=1}^N t_n = \frac{N_1}{N_1 + N_2} = \frac{N_1}{N} \\ 1 - q = \frac{N_2}{N} \]

Como intuitivamente se puede esperar la probabilidad de pertenecer a una clase es la razón del número de miembros de esa clase sobre el total.

Clasificación con dos clases

Tomando derivadas con respecto a \(\mu_1\), igualando a cero; y después con respecto a \(\mu_2\):

\[ \mu_1 = \frac{1}{N} \sum_{n=1}^{N} x_n t_n \\\ \mu_2 = \frac{1}{N} \sum_{n=1}^{N} x_n (1-t_n) \]

La media para la clase \(C_1\) está formada por la contribución de los miembros de esa clase, y lo mismo para la clase \(C_2\).

Clasificación con dos clases

Finalmente, tomando la derivada con respecto a \(\Sigma\) e igualando a cero:

\[ \Sigma = \frac{N_1}{N} S_1 + \frac{N_2}{N} S_2 \]

Donde:

\[ S_1 = \frac{1}{N_1} \sum_{n \in C_1} (x_n - \mu_1)(x_n-\mu_1)^T \\ S_2 = \frac{1}{N_2} \sum_{n \in C_2} (x_n - \mu_2)(x_n-\mu_2)^T \]

Aplicación a los datos de Howell

Cálculos manuales

Hagamos los cálculos con los datos de Howell y las expresiones anteriores:

mu_1 =  [ 48.59028695 160.35847636]
mu_2 =  [ 41.81419014 149.51351872]
Sigma = 
[[30.66102388 19.43413315]
 [19.43413315 30.30930878]]
theta0 =  -55.96595497063919
theta =  [-0.00975935  0.3640671 ]

Cálculos con scikit-learn

Ahora utilicemos la implementación de scikit-learn.

X = adultos[["weight", "height"]]
y = adultos["male"]
regresion_logistica = LogisticRegression()
regresion_logistica.fit(X, y)
print(regresion_logistica.intercept_)
print(regresion_logistica.coef_)

[-54.48965293]
[[-0.02001189  0.35686554]]

Y recordemos el cálculo manual

theta0 =  -55.96595497063919
theta =  [-0.00975935  0.3640671 ]

Los números se parecen pero no son exactamente iguales.

Cálculos con scikit-learn

¿Por qué no son exactamente iguales? Porque scikit-learn utiliza otra estrategia para encontrar el mínimo: descenso de gradiente.

Para ello hemos de utilizar un función de pérdidas. Esta vez utilizamos como función de pérdidas la máxima verosimilitud de los datos:

\[ \mathcal{L}(\theta) = \prod_{n=1}^N \sigma(\theta^T x_n)^{t_n}(1 - \sigma(\theta^T x_n))^{1-t_n} \]

Esta es la expresión que tenemos que maximizar con respecto de \(\theta\).

Cálculos con scikit-learn

Y como ya sabemos es siempre más fácil trabajar con sumas que con productos, tomamos el logaritmo y cambiamos el signo:

\[ -log(\mathcal{L}(\theta)) = -\sum_{n=1}^N t_n \ln \sigma(\theta^T x_n) + (1 - t_n) \ln(1 - \sigma(\theta^T x_n)) \]

Esta es la expresión que se debe minimizar (hemos cambiado el signo), con la misma técnica que aplicamos en el caso de la regresión lineal.

\[ \theta^{i+1} = \theta^i - \eta \frac{\partial \mathcal{L(\theta)}}{\partial \theta}; \: \mathcal{L(\theta^{i+1}}) < \mathcal{L(\theta^i)} \]

Cálculos con scikit-learn

La derivada de la función sigmoide es:

\[ \frac{d \sigma(x)}{d x} = \sigma(x)(1 - \sigma(x)) \]

Con lo que la derivada de la función de pérdidas queda como: \[ - \frac{\partial (log\mathcal{L}(\theta))}{\partial \theta} = \sum_{i=1}^N (\sigma(\theta^T x) - t_n)x_n \]

Resultados

Aplicación a Howell

Vamos a aplicar, de modo más sistemático, lo que hemos aprendido al conjunto de datos de Howell.

Empezamos dividiendo nuestro conjunto de datos en conjunto de entrenamiento y conjunto de prueba, y entrenamos con el conjunto de prueba:

random_state = 69
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=random_state)
logistic_regression = LogisticRegression(random_state=random_state)
logistic_regression.fit(X_train, y_train)

Aplicación a Howell

Ahora aplicamos el modelo al conjunto de pruebas y visualizamos.

y_pred = logistic_regression.predict(X_test)
confusion_mat = confusion_matrix(y_test, y_pred)
ConfusionMatrixDisplay(confusion_mat).plot()
RocCurveDisplay.from_estimator(logistic_regression, X_test, y_test);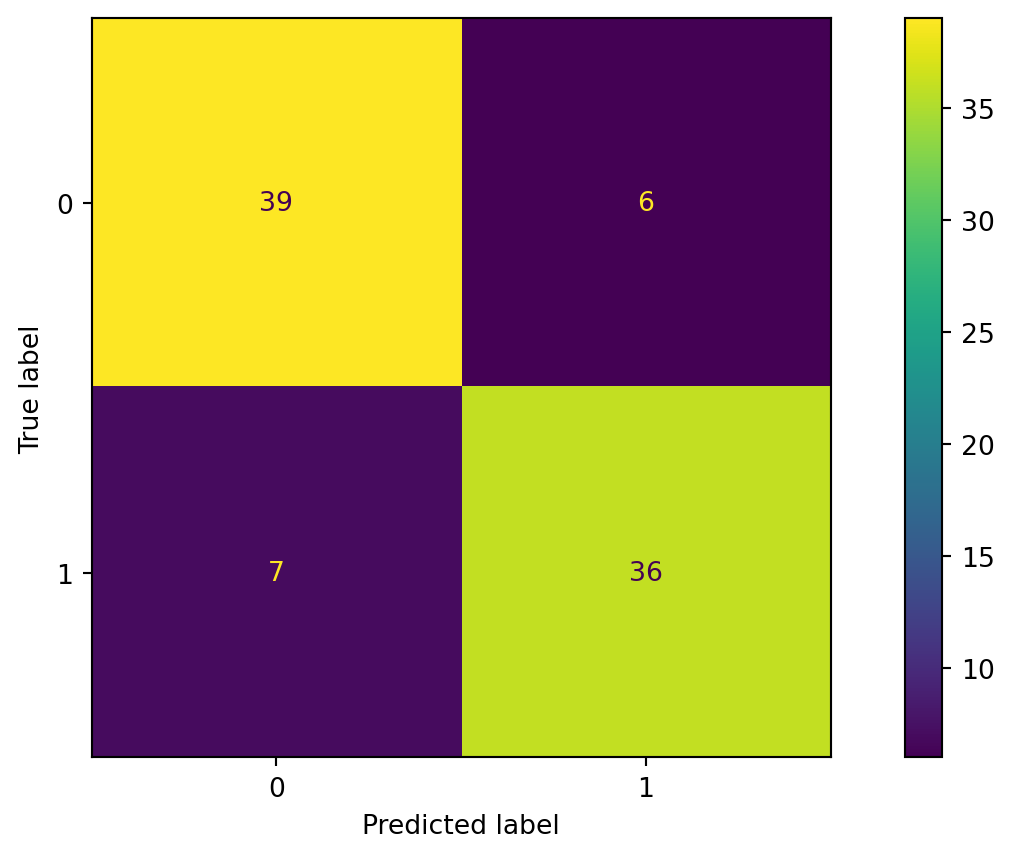

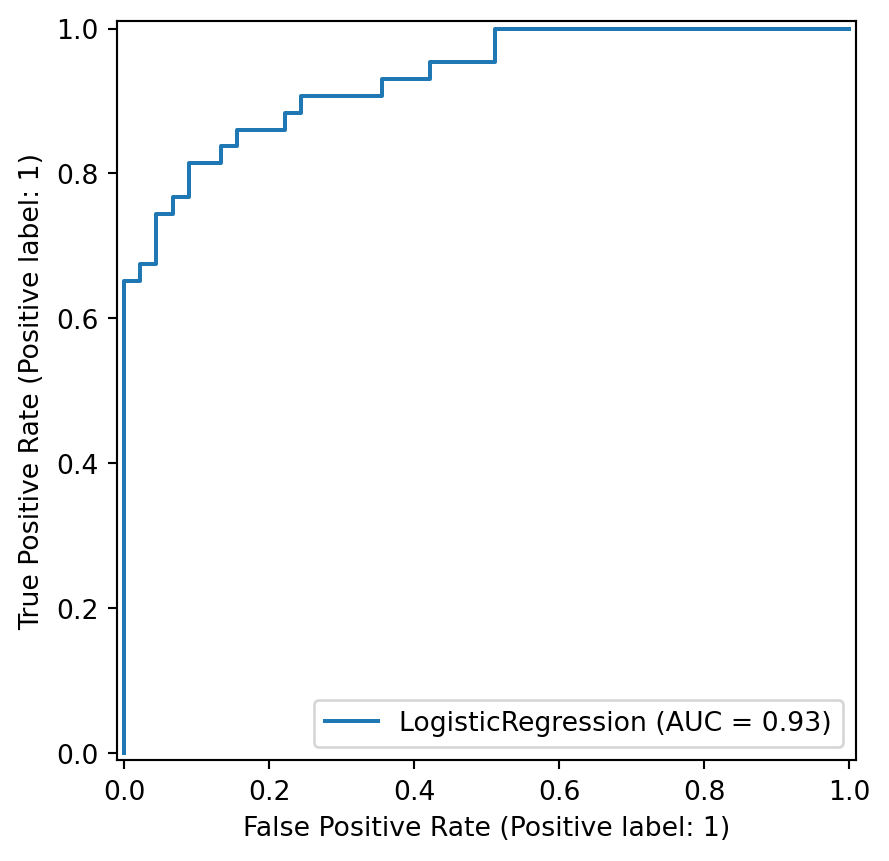
Aplicación a Howell

El Área Bajo la Curva (Area Under Curve) es del 93%, no está mal.

Ya que no hay muchos datos en el conjunto Howell, vamos a realizar una validación cruzada repitiendo 10 veces el ajuste y la prueba:

scores = cross_val_score(logistic_regression, X, y, cv=15)
print("Media de la precisión: ", scores.mean(), ", desviación estándar: ", 
    scores.std())

Media de la precisión:  0.854951690821256 , desviación estándar:  0.07762553738452942

El modelo nos da una precisión del 85%.

Aplicación a Howell

Para acabar una pequeña curiosidad. Visualicemos los datos como una sigmoide diferenciando por género.

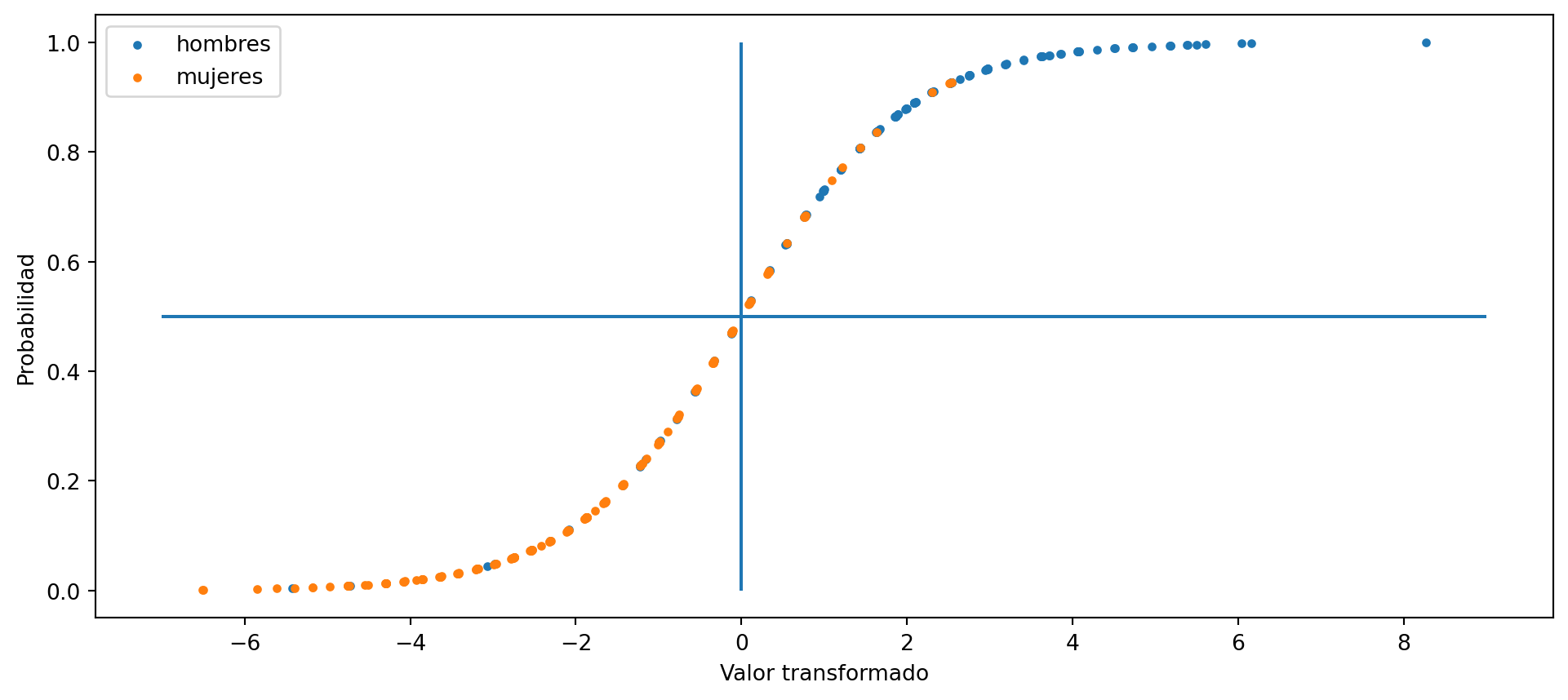
Resumen

La regresión logística es un algoritmo de clasificación.
La regresión logística funciona muy bien si los datos siguen una distribución gaussiana y sus matrices de covarianza son iguales.
Para deducir las fórmulas hemos utilizado el teorema de Bayes y el principio de máxima verosimilitud.
También hemos deducido la función de pérdidas sobre la que se puede aplicar la técnica de descenso de gradiente.

Resumen

Es importante comprobar que nuestros datos cumplen con las condiciones de normalidad e igualdad de matrices de covarianza.