Regresión Lineal

Óscar Belmonte Fernández

Contenidos

• Formula exacta de la Regresión Lineal
• Regresión lineal múltiple
• Regresión polinomial
• Descenso de gradiente
• Regularización
• Resumen

Introducción

La regresión lineal es uno de los algoritmos para problemas de regresión más antiguos y utilizados.

No obstante hay que conocer en qué problemas se puede utilizar y en qué otros no se puede utilizar.

La regresión lineal simple se puede extender, de manera muy sencilla, a problemas de regresión con múltiples variables y regresión con polinomios.

Introducción

Aunque existe una formula exacta para resolver problemas de regresión, estudiaremos la técnica del descenso de gradiente para encontrar la solución de la regresión lineal.

Finalmente veremos qué es la regularización y qué problema nos ayuda a resolver.

Objetivos de aprendizaje

• Decidir cuando en un problema se puede emplear la regresión lineal.
• Estimar la bondad de un ajuste con regresión lineal.
• Demostrar el fundamente del descenso de gradiente.
• Razonar si la regularización es apropiada para un determinado problema.
• Construir una solución de regresión (múltiple, polinómica).

Referencias

• Hands-on Machine Learning. Capítulos 1 y 4.
• Pattern recognition and Machine Learning. Capítulo 3.

Formula exacta de la Regresión Lineal

Objetivo de la regresión lineal

La hipótesis de partida es que existe una relación lineal entre una variable que se utiliza como predictor (\(x\)), y la salida (\(y\)):

\[ h_{\theta}(x) = y = \theta_0 + \theta_1 x + \epsilon \]

Donde \(\epsilon \sim N(0,\sigma^2)\) sigue una distribución normal, con media 0 y varianza \(\sigma^2\).

Objetivo de la regresión lineal

Es decir, tengo un conjunto de \(n\) datos para los cuales:

\[ h_{\theta}(x_1) = y_1 = \theta_0 + \theta_1 x_1 + \epsilon \\ h_{\theta}(x_2) = y_2 = \theta_0 + \theta_1 x_2 + \epsilon \\ ... \\ h_{\theta}(x_N) = y_N = \theta_0 + \theta_1 x_N + \epsilon \\ \]

Que podemos expresar de manera matricial como:

\[ h_{\theta}(\mathbf{X}) = \mathbf{y} = \mathbf{X \theta} + \mathbf{\epsilon} \]

Objetivo de la regresión lineal

\[ h_{\theta}(\mathbf{X}) = \mathbf{y} = \mathbf{X \theta} + \mathbf{\epsilon} \]

Donde:

\[ \begin{bmatrix} y_1 \\ y_2\\ ...\\ y_N \\ \end{bmatrix} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ ...\\ 1 & x_N \\ \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \\ \end{bmatrix} + \begin{bmatrix} \epsilon \\ \epsilon \\ ... \\ \epsilon \\ \end{bmatrix} \]

En aprendizaje automático se utilizan vectores columna.

Objetivo de la regresión lineal

El objetivo de la regresión lineal es, encontrar unos estimadores de \(\theta\) que vamos a escribir como \(\hat \theta\), de tal modo que los \(\hat y\) que obtengo al utilizar esos estimadores:

\[ \begin{bmatrix} \hat y_1 \\ \hat y_2\\ ...\\ \hat y_N \\ \end{bmatrix} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ ...\\ 1 & x_N \\ \end{bmatrix} \begin{bmatrix} \hat \theta_0 \\ \hat \theta_1 \\ \end{bmatrix} \]

están a la menor distancia posible de los datos \(y\).

Objetivo de la regresión lineal

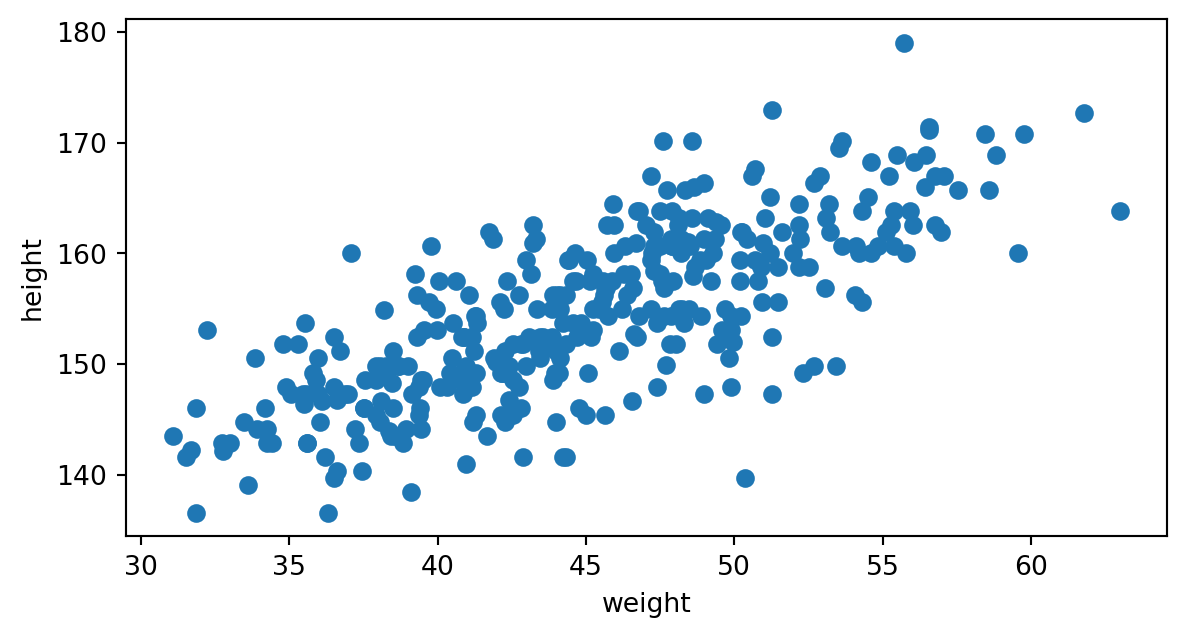
Veamos un caso real, la relación entre el peso y la altura de los nativos adultos de la etnia !Kung San.

\[ height = h_{\theta}(weight) = \theta_0 + \theta_1 weight + \epsilon \]

A partir del predictor (weight) queremos obtener el valor de la altura (height) en cm.

Función de pérdidas \(\mathcal{L}(h_\mathbf{\theta})\)

El objetivo es encontrar los parámetros \(\theta\) que minimizan la distancia entre los datos reales \(y_i\) y los valores calculados \(h_{\theta}(x_i)\).

\[ \mathcal{L}(h_\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - \hat y_i \rvert ^2 \]

donde hemos utilizado el cuadrado de la distancia euclídea (norma \(l_2\)) entre los datos del conjunto \(y_i\) y los valores obtenidos con el modelo lineal \(\hat y_i\).

Que se puede expresar en forma matricial como:

\[ \mathcal{L_{\theta}} = \frac{1}{N} \lVert \mathbf{y} - \mathbf{X \theta} \rVert^2 \]

Minimizar la función de pérdidas

Tenemos que encontrar el mínimo de la función de pérdidas.

Tomamos las derivadas parciales respecto a los parámetros \(\mathbf{\theta}\) \[ \vec\nabla_{\mathbf{\theta}}\mathcal{L} = \vec\nabla_{\mathbf{\theta}} \lVert \mathbf{y} - \mathbf{X \theta} \rVert^2 = 0 \]

y llegamos a la expresión matricial:

\[ \mathbf{\theta} = \frac{\mathbf{X^Ty}}{\mathbf{X^T X}} = (\mathbf{X^T X})^{-1}\mathbf{X^Ty} \]

Pregunta: ¿La matriz \(\mathbf{X^T X}\) es siempre invertible?

Minimizar la función de pérdidas

Aplicando el cálculo a nuestros datos, obtenemos la recta de regresión:

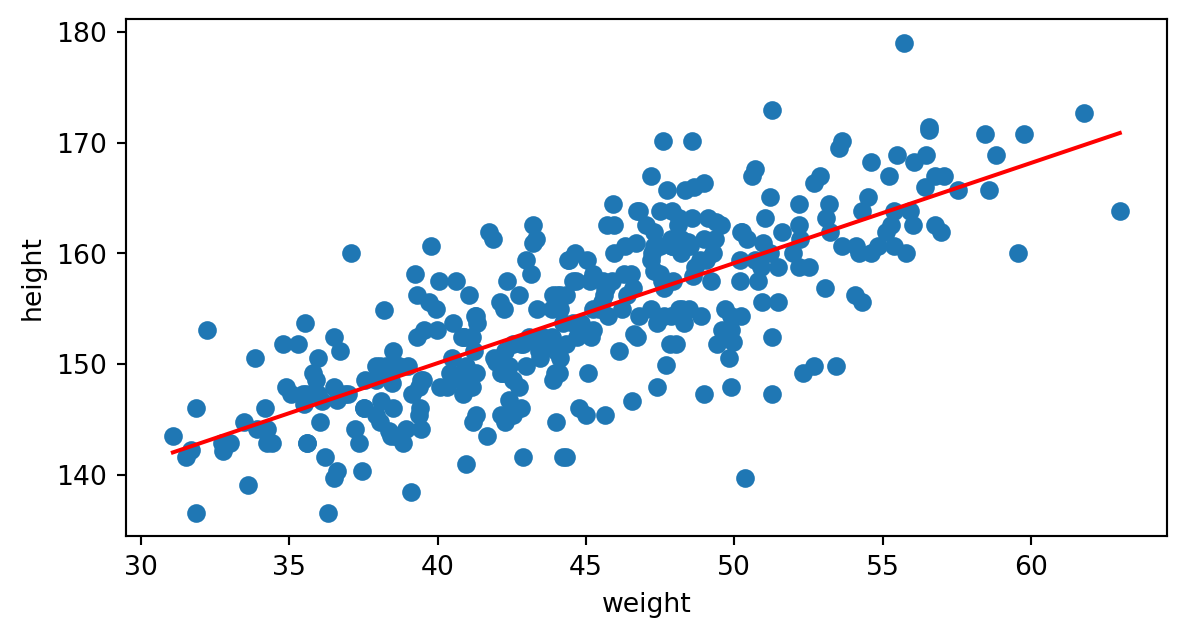
Con \(\hat \theta_0 = 113.8794\) y \(\hat \theta_1 = 0.9050\).

Residuos

Los residuos son la parte no lineal de los datos, hemos supuesto que siguen una distribución normal:

\[ r_i = y_i - h_{\theta}(x_i) \]

Residuos

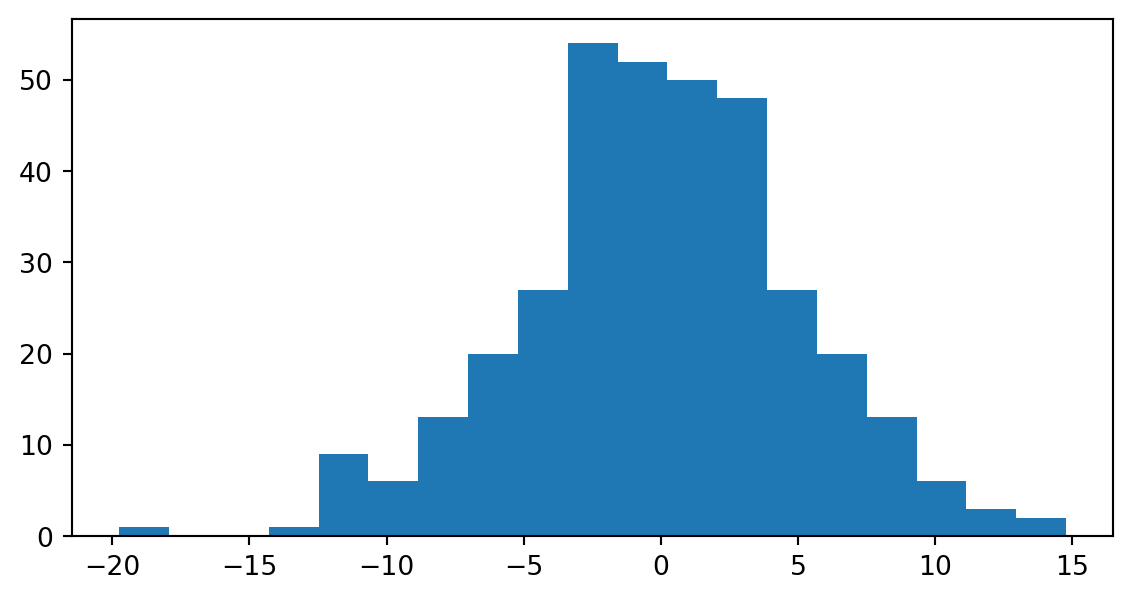
Distribución de los residuos

Varianza de los residuos

La varianza de los residuos es la contribución de \(\epsilon \sim N(0,\sigma^2)\).

Un estimador para la varianza de los residuos es:

\[ {\hat \sigma}^2 = \frac{1}{N} \sum_{i=1}^N (y_i - h_{\theta}(x_i))^2 \]

Error estándar de \(\mathbf{\theta}\)

Un estimador sin sesgo (unbiased) para \(\sigma^2\) lo podemos calcular como:

\[ MSE = \frac{1}{N-2} \sum_{i=1}^N (y_i - h_{\theta}(x_i))^2 \]

ya que tenemos sólo \(N-2\) grados de libertad.

Error estándar de \(\mathbf{\hat \theta}\)

El error estándar del parámetro estimado \(\hat \theta_0\) se calcula como:

\[ SE(\hat \theta_0) = \sqrt{MSE \left(\frac{1}{n} + \frac{\bar x^2}{S_{xx}}\right)} \]

donde \(S_{xx} = \sum_{i=1}^N (x_i - \bar x)^2\) es la varianza de los datos.

El error estándar del parámetro estimado \(\hat \theta_1\) se calcula como:

\[ SE(\hat \theta_1) = \sqrt{\frac{MSE}{S_{xx}}} \]

Error estándar de \(\mathbf{\hat \theta}\)

En el ejemplo que estamos tratando, al aplicar las fórmulas, obtenemos \(SE(\hat \theta_0) = 1.9111\) y \(SE(\hat \theta_1) = 0.0420\).

Finalmente:

\[ \hat \theta_0 = 113.9 \pm 1.9 \]

\[ \hat \theta_1 = 0.90 \pm 0.04 \]

Normalidad de los residuos

Ahora debemos comprobar la hipótesis de normalidad de los residuos, sin ella la regresión lineal no tiene sentido.

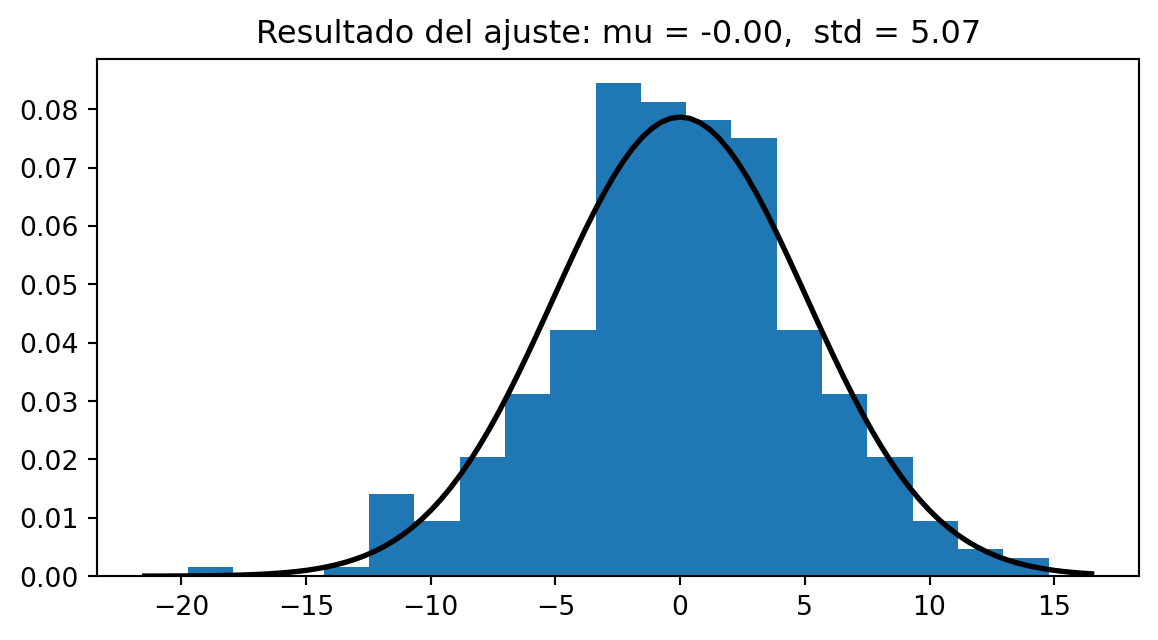
Normalidad de los residuos

Podemos aplicar el test de d’Agostino-Pearson, que nos da un p-valor de \(p = 0.0721\).

O el test de Shapiro-Wilk, que nos da un p-valor de \(p = 0.2499\).

En ambos caso del p-valor es mayor que \(0.05\), luego no podemos descartar que los residuos sigan una distribución normal.

Normalidad de los residuos

Otra prueba gráfica que podemos utilizar son los qqplot o gráficos cuantil-cuantil.

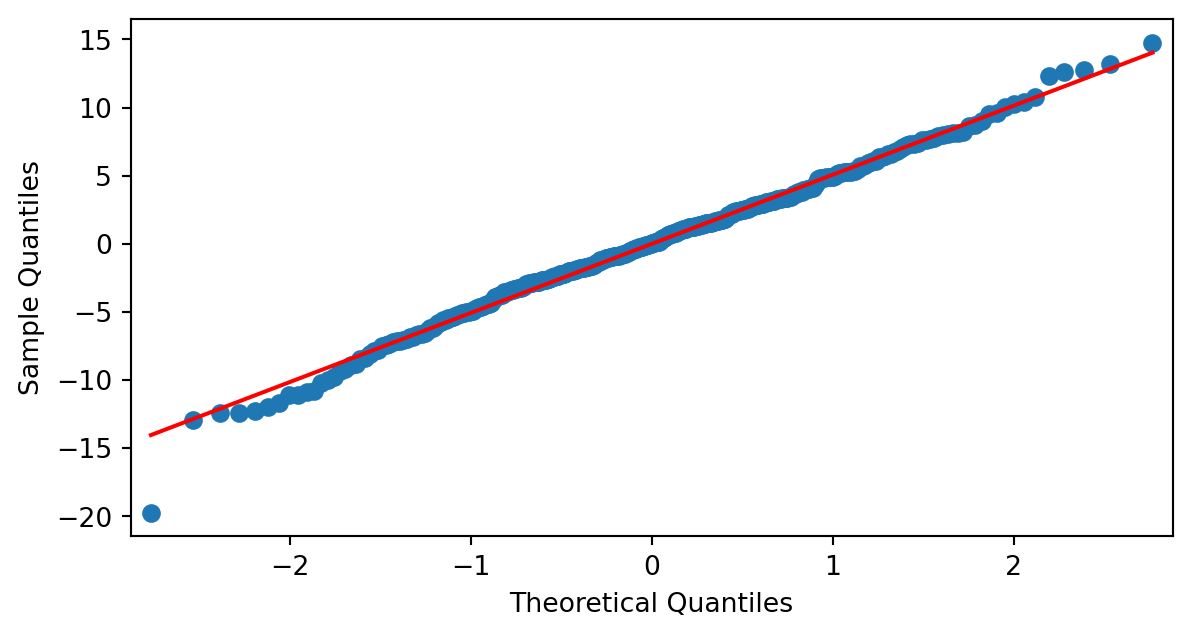
Si podemos apreciar que el gráfico qqplot es una recta no podemos descartar que nuestros datos sigan una distribución normal.

¿Cuál es la linealidad de nuestros datos?

El coeficiente de determinación (\(R^2\)) nos da una idea de la varianza de los datos que puede explicar el modelo.

Suma de los cuadrados de los residuos: \(SS_{res} = \sum_{i=1}^N(y_i - h_\theta(i))^2\)

Suma total de los cuadrados: \(SS_{tot} = \sum_{i=1}^N(y_i - \bar{y})^2\)

\[R^2 = 1 - \frac{SS_{res}}{SS_{tot}}\]

La fracción \(\frac{SS_{res}}{SS_{tot}}\) es la fracción de la varianza no explicada por los datos.

En nuestros caso \(R^2 = 0.5696\) y la varianza no explicada es \(0.4303\).

¿Cuál es la linealidad de nuestros datos?

Otra medida de la linealidad de los datos, es el coeficiente de correlación de Pearson, que no es más que la raíz cuadrada de \(R^2\):

\[\rho = \sqrt{R^2}\]

En nuestro caso obtenemos \(\rho = 0.7547\).

Como criterio general, se considera que el ajuste es bueno cuando este valor está por encima de 0.7.

En resumen

1. Hemos supuesto que existe una relación lineal entre el predictor (peso) y la variable predicha (altura).
2. Hemos supuesto que los residuos de nuestros datos siguen una distribución normal con media \(\mu = 0\) y varianza \(\sigma^2\)
3. Hemos calculado los valores estimados para \(\theta_0,\theta_1,\sigma\).
4. Hemos calculado sus errores estándar.
5. Hemos ajustado los residuos a una normal.
6. Hemos hecho pruebas para comprobar la bondad del ajuste.
7. Hemos utilizado un gráfico cuantil-cuantil.

Paquetes de Python

Estos resultados, y algunos más, los podemos obtener con el paquete statsmodels

import statsmodels.formula.api as smf
import statsmodels.api as sm

modelo = smf.ols(formula='height ~ weight', data=adults).fit()
print(modelo.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                 height   R-squared:                       0.570
Model:                            OLS   Adj. R-squared:                  0.568
Method:                 Least Squares   F-statistic:                     463.3
Date:                Wed, 11 Dec 2024   Prob (F-statistic):           4.68e-66
Time:                        18:37:07   Log-Likelihood:                -1071.0
No. Observations:                 352   AIC:                             2146.
Df Residuals:                     350   BIC:                             2154.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept    113.8794      1.911     59.589      0.000     110.121     117.638
weight         0.9050      0.042     21.524      0.000       0.822       0.988
==============================================================================
Omnibus:                        5.258   Durbin-Watson:                   1.959
Prob(Omnibus):                  0.072   Jarque-Bera (JB):                5.729
Skew:                          -0.180   Prob(JB):                       0.0570
Kurtosis:                       3.511   Cond. No.                         321.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Paquetes de Python

El modelo de regresión lineal también lo encontramos en el paquete scikit-learn, junto con medidas de error y otros indicadores como \(R2\)

from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score

modelo_lineal = linear_model.LinearRegression()
X = weight
y = height
modelo_lineal.fit(X, y)
y_predict = modelo_lineal.predict(X)
print("MSE: ", mean_squared_error(y, y_predict))
print("R2: ", r2_score(y, y_predict))

MSE:  25.72382477809007
R2:  0.5696443654975303

Paquetes de Python

En el caso anterior, estamos utilizando el mismo conjunto de datos para entrenar el modelo, que para calcular el error del modelo sobre los datos.

Usualmente se utilizan dos conjuntos de datos, con uno de ellos entrenamos el modelo y el otro conjunto de datos lo utilizamos para calcular el error del modelo.

Paquetes de Python

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=69)
modelo_lineal = linear_model.LinearRegression()
modelo_lineal.fit(X_train, y_train)
y_predict = modelo_lineal.predict(X_test)
print("MSE: ", mean_squared_error(y_test, y_predict))
print("R2: ", r2_score(y_test, y_predict))

MSE:  22.857368238528068
R2:  0.6480326131296372

Fíjate en que hemos utilizado el parámetro random_state=69 para fijar el inicio de la generación de números aleatorios, y que los resultados sean reproducibles.

Paquetes de Python

En nuestro caso, además, el número de muestras no es muy elevado, por lo que el error puede depender de la división particular que hagamos para obtener el conjunto de entrenamiento y el de pruebas.

En este caso la recomendación es dividir varias veces el conjunto original, entrenar, calcular el error, y promediar el resultado.

from sklearn.model_selection import cross_val_score

scores = cross_val_score(modelo_lineal, X, y, cv=5, scoring="mean_squared_error")
print(scores)
print("Media: ", scores.mean(), ", std: ", scores.std())

[27.74141409 32.41805083 23.28533277 15.19936772 31.83726912]
Media:  26.0962869056722 , std:  6.3604139836175655

Estimación de parámetros por máxima verosimilitud

Para terminar con esta sección vamos a ver cómo la expresión de la función de pérdidas: \[ \mathcal{L}(h_\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - x_i\theta \rvert ^2 \]

aparece de modo natural al asumir que los residuos están normalmente distribuídos.

Estimación de parámetros por máxima verosimilitud

Hemos supuesto que los residuos siguen un distribución normal independientemente del punto donde calculamos la regresión, lo que significa suponer que:

\[ p(y_i|\theta,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(y_i-x_i\theta)^2}{2\sigma^2}} \]

Estimación de parámetros por máxima verosimilitud

Un estimador máximo verosímil es aquel que maximiza la función de verosimilitud, que no es más que el producto de las probabilidades de cada una de las muestras. Si suponemos que las variables de la muestra son independientes y siguen la misma distribución de probabilidad (iid: independientes e idénticamente distribuidas):

\[ p(\mathbf{y}|\theta,\sigma^2) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(y_i-x_i\theta)^2}{2\sigma^2}} \]

donde hemos extendido el productorio a todas las muestas.

Estimación de parámetros por máxima verosimilitud

Si tomamos logaritmos de la función de verosimilitud:

\[ ln(p(\mathbf{y}|\theta,\sigma^2)) = {-\frac{1}{2}}\sum_{i=1}^N ln(2\pi\sigma^2) - \sum_{i=1}^N \frac{(y_i-x_i\theta)^2}{2\sigma^2} \]

Como la función logaritmo es monótonamente creciente maximizar la función de verosimilitud es lo mismo que minimizar la misma función cambiada de signo.

Estimación de parámetros por máxima verosimilitud

\[ -ln(p(\mathbf{y}|\theta,\sigma^2)) = {\frac{1}{2}}\sum_{n=1}^N ln(2\pi\sigma^2) + \boxed{\sum_{i=1}^N \frac{(y_i-x_i\theta)^2}{2\sigma^2}} \]

Si fijamos \(\sigma^2\) minizar la expresión anterior significa minimizar el sumatorio que depende de \(\theta\), que es proporcional a la función de pérdidas.

Estimación de parámetros por máxima verosimilitud

Por otro lado, podemos calcular el estimador máximo verosímil derivando la expresión anterior con respecto a \(\sigma^2\) e igualando a cero, con lo que obtenemos:

\[ \hat \sigma^2 = \frac{1}{N} \sum_{i=1}^N (y_i - x_i\theta)^2 \]

Que es exactamente el estimador con sesgo que ya habíamos calculado (Demostración).

Regresión lineal múltiple

Extensión de la regresión lineal

Hasta ahora, sólo hemos utilizado una característica como predictor en nuestro modelo.

Pero, podemos añadir más características como predictores de nuestro modelo. \[ h_{\theta}(x) = y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 +...+ \epsilon \]

Extensión de la regresión lineal

Nuestro conjunto de datos es:

	height	weight	age	male
0	151.765	47.825606	63.0	1
1	139.700	36.485807	63.0	0
2	136.525	31.864838	65.0	0
3	156.845	53.041914	41.0	1

Vamos a incluir el peso, edad y género para estimar la altura:

\[ height = \theta_0 + \theta_1 weight + \theta_2 age + \theta_3 male + \epsilon \]

Extensión de la regresión lineal

Fíjate en que lo que estamos haciendo es añadir más columnas a la matriz de los predictores:

\[ \begin{bmatrix} y_1 \\ y_2\\ y_3\\ ...\\ y_N \\ \end{bmatrix} = \begin{bmatrix} 1 & x_1^1 & x_1^2 & ... & x_1^m\\ 1 & x_2^1 & x_2^2 & ... & x_2^m\\ 1 & x_3^1 & x_3^2 & ... & x_3^m\\ ... & ... & ... & ... & ... \\ 1 & x_n^1 & x_n^2 & ... & x_N^m\\ \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ ...\\ \theta_m \\ \end{bmatrix} + \begin{bmatrix} \epsilon \\ \epsilon \\ \epsilon \\ ... \\ \epsilon \\ \end{bmatrix} \]

Extensión de la regresión lineal

Que podemos resolver de este modo:

modelo_lineal = linear_model.LinearRegression()
X = np.hstack([weight, age, male])
y = height
modelo_lineal.fit(X, y)
y_predict = modelo_lineal.predict(X)
print("MSE: ", mean_squared_error(y, y_predict))
print("R2: ", r2_score(y, y_predict))

MSE:  18.067146428469517
R2:  0.6977394173709526

Como vemos, ha disminuido el error cuadrático medio, y ha mejorado la medida de linealidad \(R2\).

Normalidad de los residuos

Como en el caso de regresión lineal simple, debemos comprobar la hipótesis de que los residuos se distribuyen siguiendo una distribución normal de media cero y cierta varianza.

Los parámetros del ajuste a una distribución normal son \(\mu=-4.3e-14\) y \(\sigma = 4.25\).

Pero, al realizar las pruebas de normalidad obtenemos para la prueba de d’Agostino-Pearson un p-valor=1.07e-5, y con la prueba de Shapiro-Wilk un p-valor=3.3e-4. En principio, podríamos rechazar la hipótesis nula, es decir, que los residuos siguen una distribución normal.

Normalidad de los residuos

Si utilizamos una gráfica qq-plot, vemos:

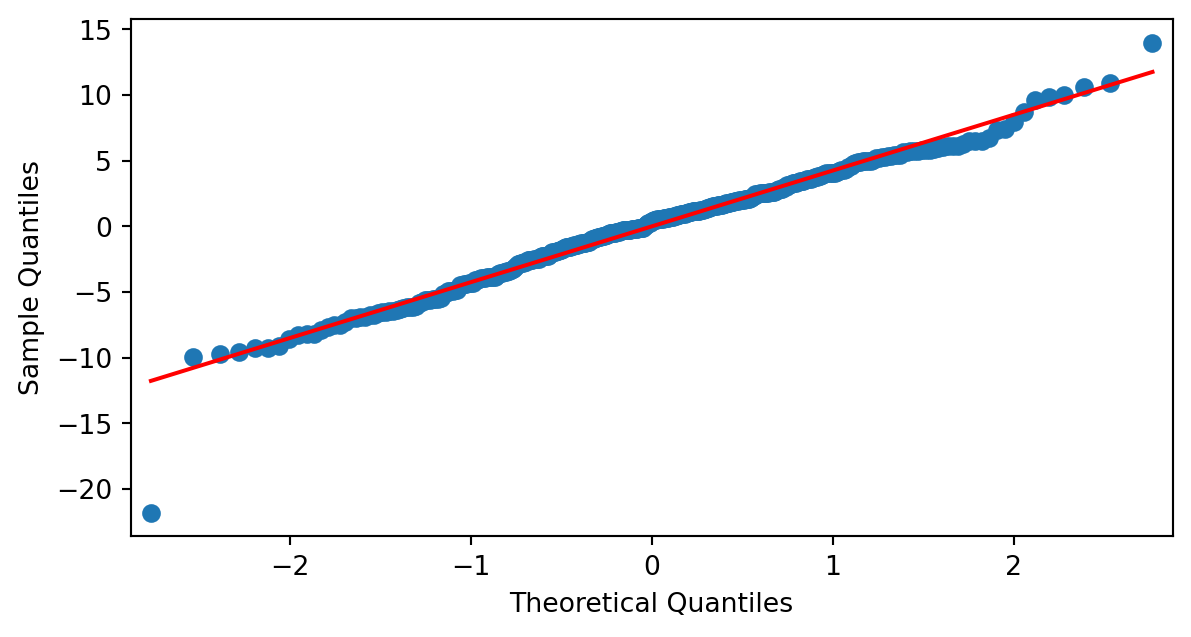
Vemos que tenemos un dato anómalo (outlier) en la parte inferior izquierda de la gráfica.

Normalidad de los residuos

Si eliminamos el dato anómalo:

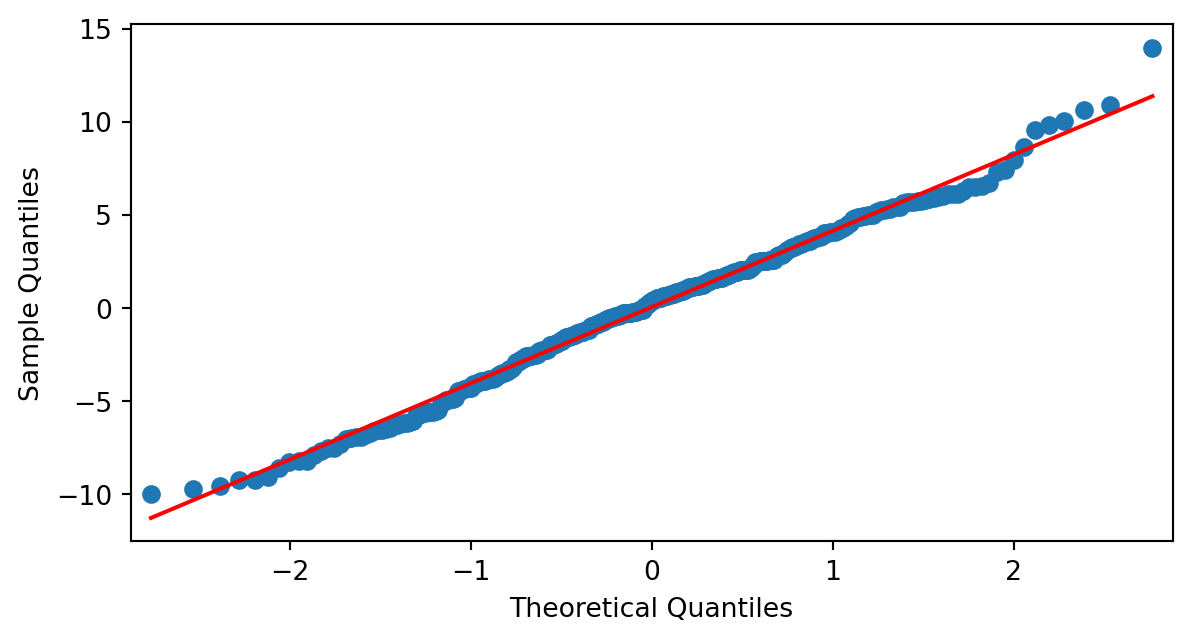
El gráfico q-q plot mejora bastante y la prueba de normalidad de d’Agostino-Pearson nos da un p-valor 0.93 y la prueba de Shapiro-Wilk un p-valor de 0.11.

Resumen

Todo lo que hemos aprendido en el caso de un único predictor y una única variable predicha lo podemos extender al caso de varios predictores y una única variable predicha.

Regresión polinomial

Extensión de la regresión lineal

Visualicemos todos los datos de nuestro cojunto:

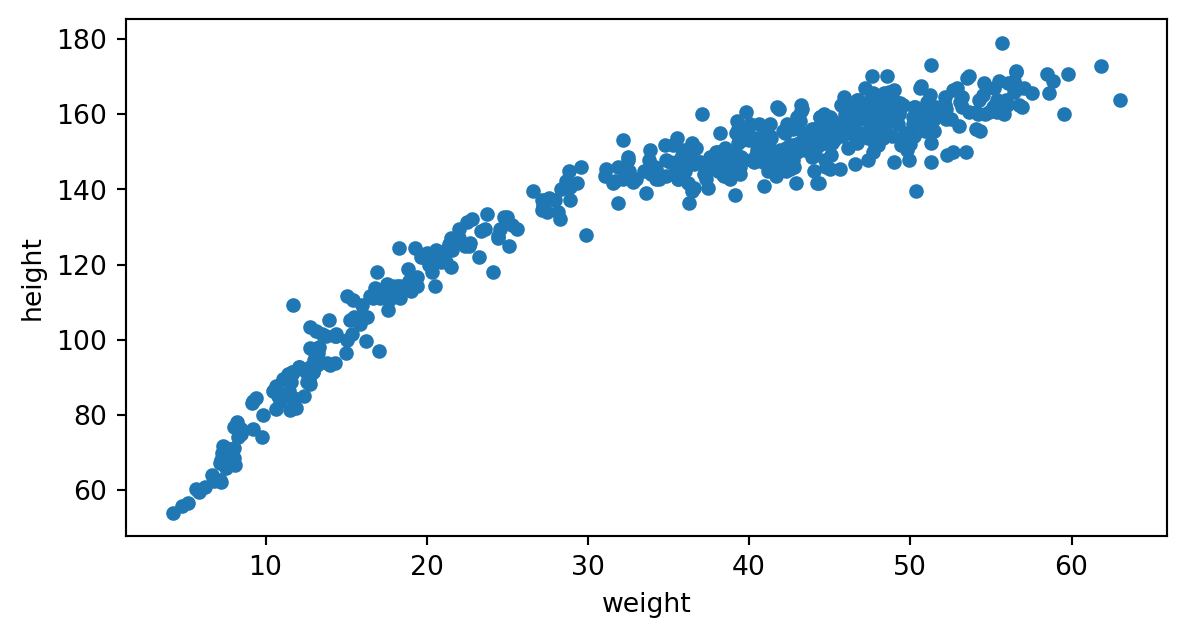
A simple vista parece que su comportamiento no es lineal.

¿Podemos utilizar un polinomio como modelo de los datos?

Extensión de la regresión lineal

En el caso de ajuste de un polinomio tenemos:

\[ h_{\theta}(x) = y = \theta_0 + \theta_1 x + \theta_2 x^2 +...+ \theta_n x^n + \epsilon \]

Fíjate en que los parámetros que buscamos \(\mathbf{\theta}\) siguen siendo lineales, no hay ninguna potencia de los parámetros, la potencia está en los datos.

Extensión de la regresión lineal

Que lo podemos expresar de modo matricial como:

\[ \begin{bmatrix} y_1 \\ y_2\\ y_3\\ ...\\ y_N \\ \end{bmatrix} = \begin{bmatrix} 1 & x_1 & (x_1)^2 & ... & (x_1)^m\\ 1 & x_2 & (x_2)^2 & ... & (x_2)^m\\ 1 & x_3 & (x_3)^2 & ... & (x_3)^m\\ ... & ... & ... & ... & ... \\ 1 & x_N & (x_N)^2 & ... & (x_N)^m\\ \end{bmatrix} \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ ...\\ \theta_m \\ \end{bmatrix} + \begin{bmatrix} \epsilon \\ \epsilon \\ \epsilon \\ ... \\ \epsilon \\ \end{bmatrix} \]

Extensión de la regresión lineal

Probemos primero un polinomio de grado 2:

MSE:  33.05986365746818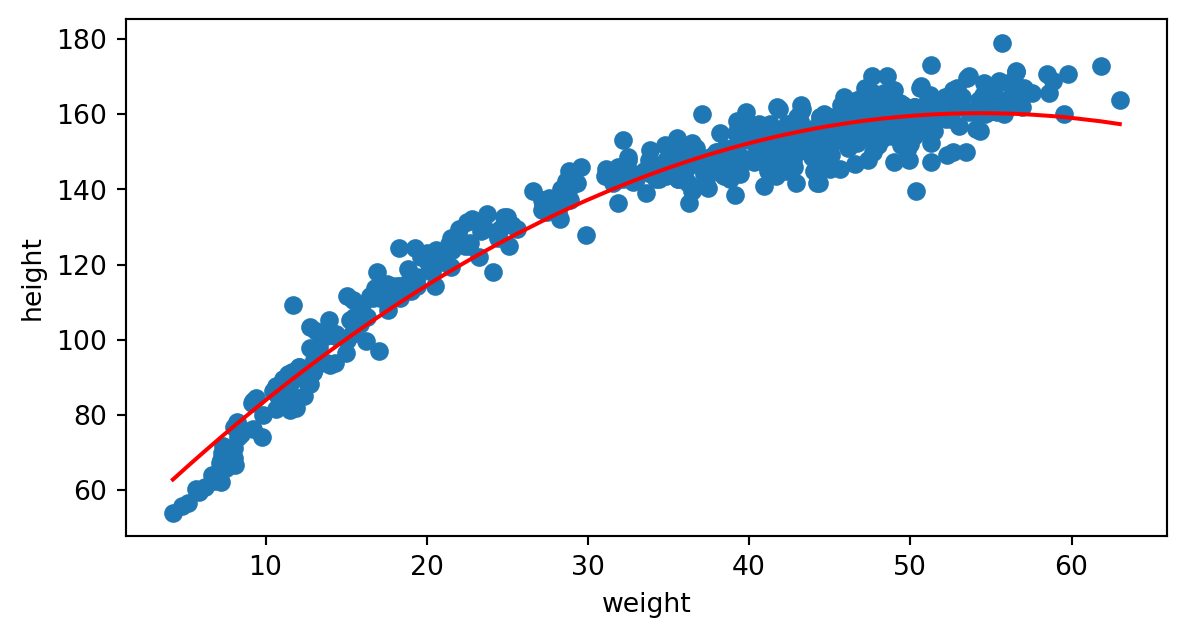

No está mal, pero quizás mejore con un polinomio de grado 3:

Extensión de la regresión lineal

MSE:  23.24163011633371

Visualmente parece mejor, y el MSE nos lo confirma.

¿Y si probamos con polinomios de otros grados? ¿Con cuál nos quedamos?

Encontrar el mejor grado del polinomio

La siguiente gráfica muestra el MSE frente al grado del polinomio:

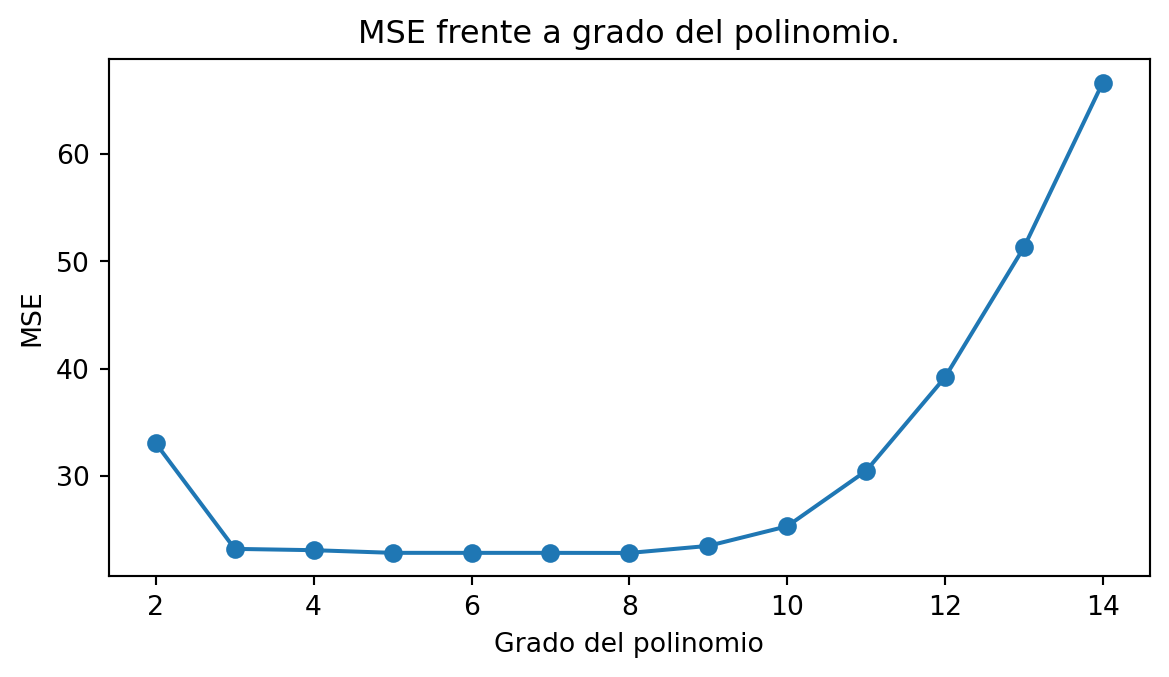
Parece que desde grado 3 hasta 9 son buenas elecciones.

Encontrar el mejor grado de un polinomio

Comprobemos la hipótesis de normalidad de los residuos para un polinomio de grado 3:

Prueba de d'Agostino-Pearson p-valor= 0.006629796639700601
Prueba de Shapiro-Wilk p-valor= 0.014143194223786298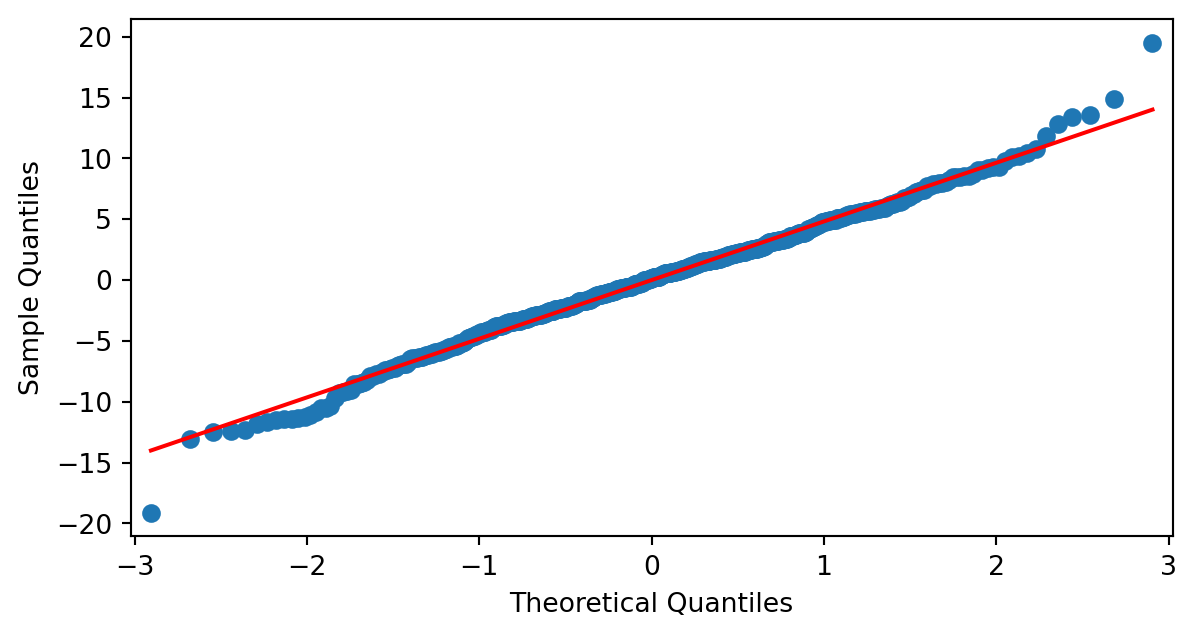

Los p-valores no están por encima del \(0.05\), pero vemos que tenemos dos datos anómalos que podemos eliminar.

Encontrar el mejor grado de un polinomio

Prueba de d'Agostino-Pearson p-valor= 0.30568678454325504
Prueba de Shapiro-Wilk p-valor= 0.11793189509486224

Esta vez, los p-valores no nos permiten rechazar la hipótesis de que los residuos están distribuidos siguiendo una distribución normal.

Encontrar el mejor grado de un polinomio

La conclusión final es que podemos utilizar un polinomio de grado 3 para ajustar nuestros datos, y obtener bastante buenos resultados.

Subajuste (underfitting)

Volvamos de nuevo al ajuste con un polinomio de grado 2:

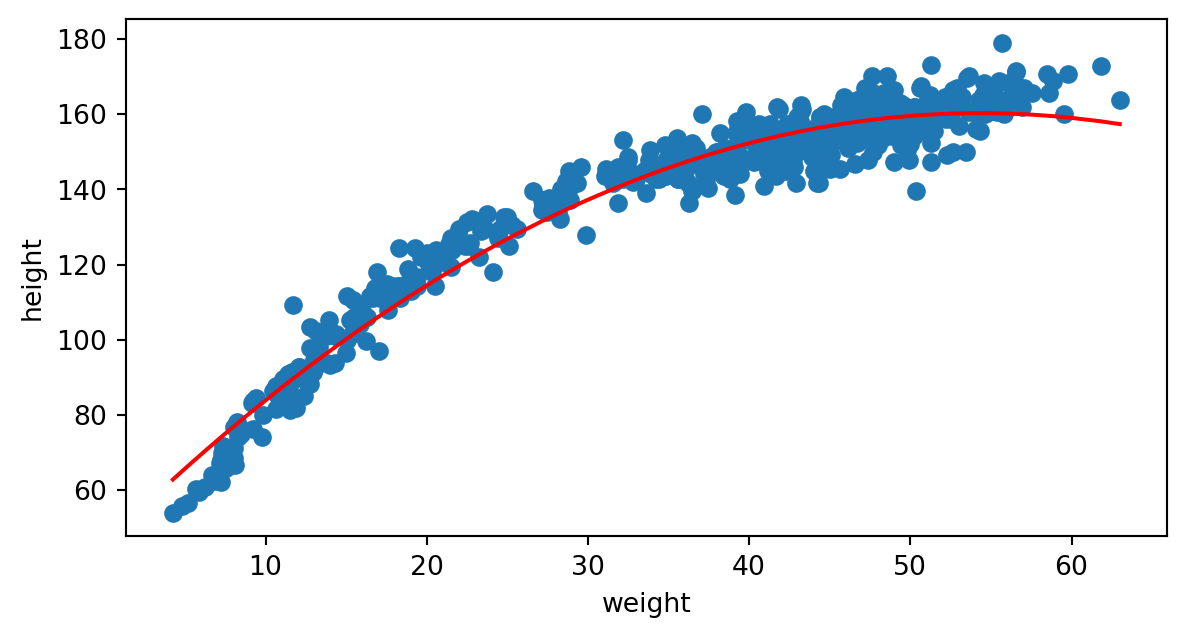
Al utilizar un polinomio de grado 2, este modelo no consigue ajustar los datos. Decimos que el modelo está subajustando los datos (underfitting).

Sobreajuste (overfitting)

Ajuste con polinomio de grado 9:

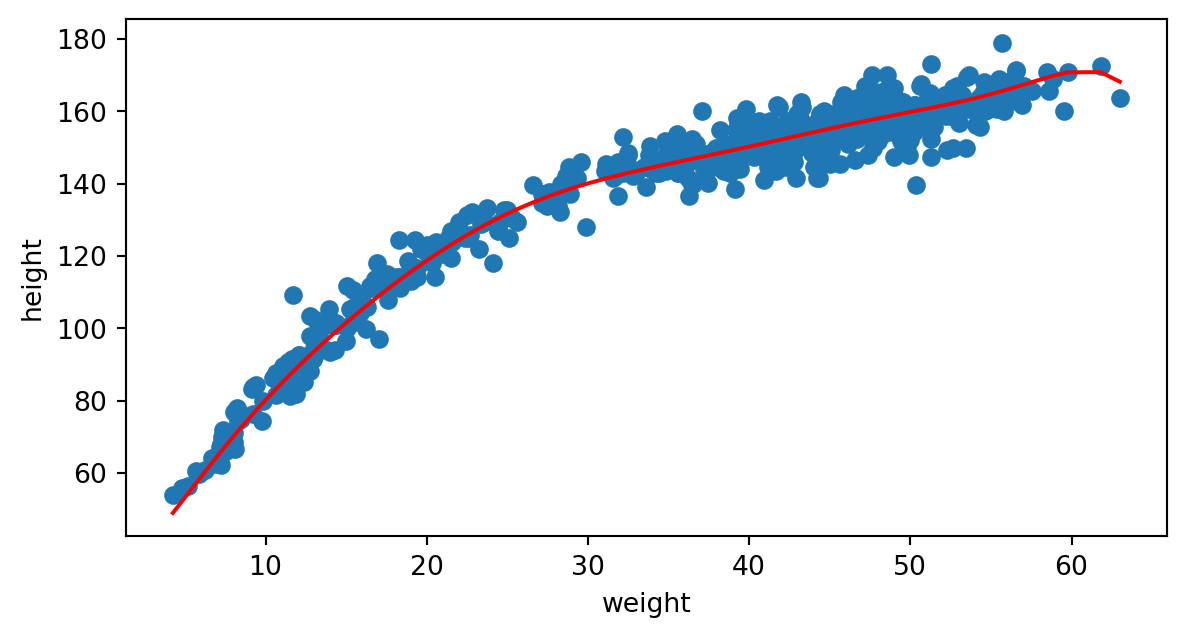
Por el contrario, si utilizamos un polinomio de grado elevado, estaremos forzando a que este polinomio se ajuste muy bien a los datos de entrenamiento, pero quizás no generalice bien.

Encontrar el mejor grado de un polinomio

En la sección de regularización veremos cómo incluir un término en la función de coste para no tener que evaluar el mejor grado de ajuste para un polinomio de modo manual.

Resumen

Fíjate en que, aumentar el grado del ajuste no es más que ampliar el número de variables predictoras. Y ya sabemos que si tenemos varias variables predictoras los análisis que podemos hacer sobre los residuos son exactamente iguales que en el caso de una única variable predictora.

Descenso de gradiente

Idea base del descenso de gradiente

En la primera parte, hemos obtenido un método directo para minimizar la función de pérdidas.

Existe otra posibilidad para «encontrar» el mínimo de la función de pérdidas. Es un proceso iterativo y se conoce como descenso del gradiente.

Vamos a verlo con detalle.

Idea base del descenso del gradiente

Volvamos a la función de pérdidas.

\[ \mathcal{L}(\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - h(\theta) \rvert ^2 \]

Lo que nos interesa es la dependencia de la función de pérdidas respecto a los parámetros \(\theta\).

Lo que queremos es, partiendo de unos valores iniciales para los parámetros \(\theta\), ir aproximándonos poco a poco a los valores de \(\theta\) que minimizan la función de pérdidas.

Idea base del descenso del gradiente

El proceso iterativo es (superíndices para indicar paso):

\[ ... \\ \mathcal{L}(\theta^i + \Delta \theta^i) < \mathcal{L}(\theta^i) \\ \theta^{i+1} = \theta^i + \Delta \theta^i \\ \mathcal{L}(\theta^{i+1} + \Delta \theta^{i+1}) < \mathcal{L}(\theta^{i+1}) \\ \theta^{i+2} = \theta^{i+1} + \Delta \theta^{i+1} \\ ... \]

y continúa hasta que se alcance un número máximo de iteraciones, o la disminución que se obtenga entre iteraciones no sea significativa.

Idea base del descenso del gradiente

Veamos cómo expresar estas ideas de modo formal. Vamos a hacer un desarrollo de Taylor de \(\mathcal{L(\theta + \Delta \theta)}\) donde \(\Delta \theta = \theta^{i+1} - \theta^i\)

\[ \mathcal{L(\theta + \Delta \theta)} = \mathcal{L(\theta)} + \frac{\partial \mathcal{L(\theta)}}{\partial \theta} \Delta \theta + \frac{1}{2!} \frac{\partial^2 \mathcal{L(\theta)}}{\partial \theta^2} (\Delta \theta)^2 + ... \]

y nos quedamos hasta el termino cuadrático en \(\Delta \theta\). Derivamos con respecto a \(\Delta \theta\) e igualamos a cero:

\[ \frac{\partial \mathcal{L(\theta + \Delta \theta)}}{\partial \Delta \theta} = \frac{\partial \mathcal{L(\theta)}}{\partial \theta} + \frac{\partial^2 \mathcal{L(\theta)}}{\partial \theta^2} \Delta \theta = 0 \]

Idea base del descenso del gradiente

\[ \Delta \theta = \theta^{i+1} - \theta^i \\ \theta^{i+1} = \theta^i - \left( \frac{\partial^2 \mathcal{L(\theta)}}{\partial \theta^2}\right)^{-1} \frac{\partial \mathcal{L(\theta)}}{\partial \theta} \]

El termino \[ \left( \frac{\partial^2 \mathcal{L(\theta)}}{\partial \theta^2}\right)^{-1} \]

es costoso de calcular, y se suele sustituir por un valor fijo \(\eta\) llamado tasa de aprendizaje.

Idea base del descenso del gradiente

Finalmente obtenemos:

\[ \theta^{i+1} = \theta^i - \eta \frac{\partial \mathcal{L(\theta)}}{\partial \theta} \\ \mathcal{L(\theta^{i+1}}) < \mathcal{L(\theta^i)} \]

es decir, calculamos el gradiente en el punto actual \(\theta^i\), lo multiplicamos por la tasa de aprendizaje \(\eta\) se lo restamos a \(\theta^i\) y obtenemos un nuevo valor \(\theta^{i+1}\) para el cuál la función de pérdidas es menor que en el paso anterior.

Idea base del descenso del gradiente

La elección de \(\eta\) se debe realizar con cuidado. Un valor grande de \(\eta\) puede dar lugar a un comportamiento errático cuando el descenso del gradiente se acerca al mínimo de la función de pérdidas.

Un valor demasiado pequeño de \(\eta\) puede dar lugar a una aproximación muy lenta al valor mínimo de la función de pérdidas.

Descenso de gradiente por lotes

Recordemos que la función de pérdidas:

\[ \mathcal{L}(\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - h(\theta) \rvert ^2 \]

utiliza todos los datos del conjunto para actualizar el valor de \(\theta^i\)

\[ \theta^{i+1} = \theta^i - \eta \frac{\partial \mathcal{L(\theta)}}{\partial \theta} \\ \mathcal{L(\theta^{i+1}}) < \mathcal{L(\theta^i)} \]

Descenso de gradiente por lotes

Si el conjunto de datos es muy numeroso y utilizamos muchos pasos en el descenso de gradiente, puede que el algoritmo tarde mucho en alcanzar el mínimo.

Descenso de gradiente estocástico

Un técnica que se suele utilizar para acelerar el proceso de convergencia del descenso de gradiente es elegir aleatoriamente una única muestra del conjunto total en cada paso del descenso.

Descenso de gradiente por mini lotes

Una técnica mixta es, para cada paso de optimización, tomar un subconjunto aleatorio de las muestras de entrenamiento.

Regularización

Qué es la regularización

Recordemos que en el caso de la regresión hemos encontrado el mejor grado del polinomio calculando error cuadrático medio.

Ahora que conocemos la técnica de descenso del gradiente, podemos ampliar la definición de la función de pérdidas para incluir un término que controle el grado del polinomio que estamos ajustando.

Modelos lineales regularizados: Ridge

En este tipo de regularización, a la función de pérdidas se le añade un término con el módulo

\[ \mathcal{L}(\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - h(\theta) \rvert ^2 + \lambda \theta^T\theta \]

Este caso tiene una solución exacta para \(\theta\):

\[ \theta = (X^TX + \lambda I)^{-1} X^T y \]

Modelos lineales regularizados: Ridge

Veamos un ejemplo sobre un subconjunto de nuestros datos cuando ajustamos a un polinomio de grado 9:

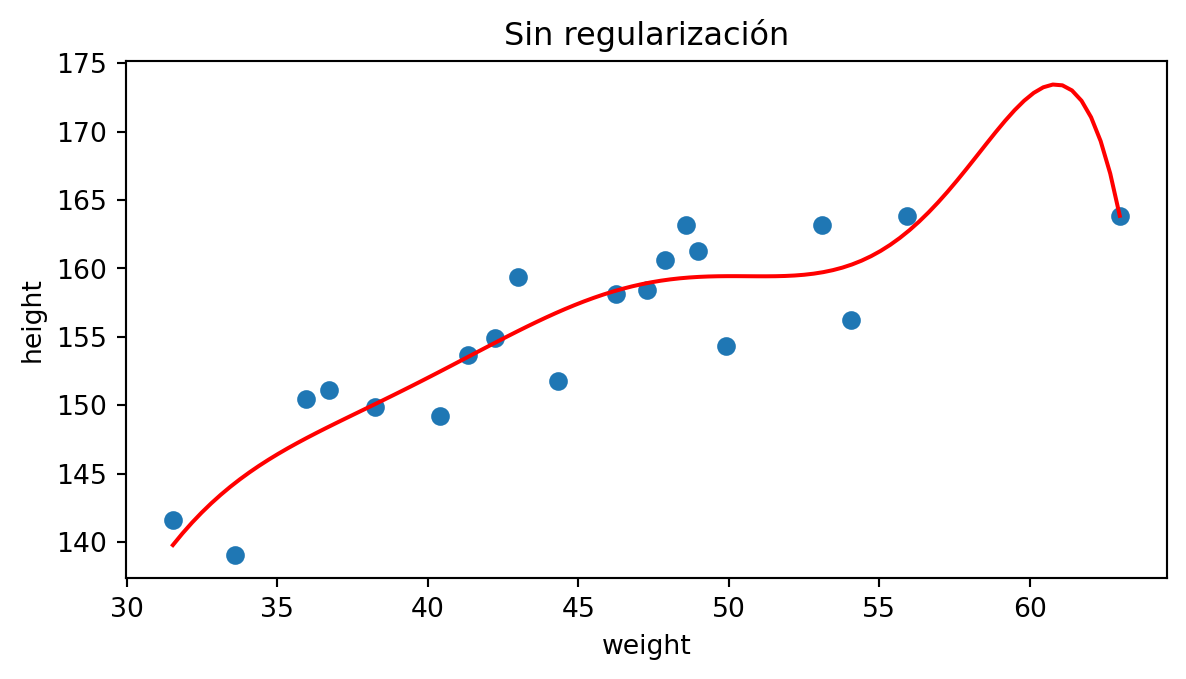
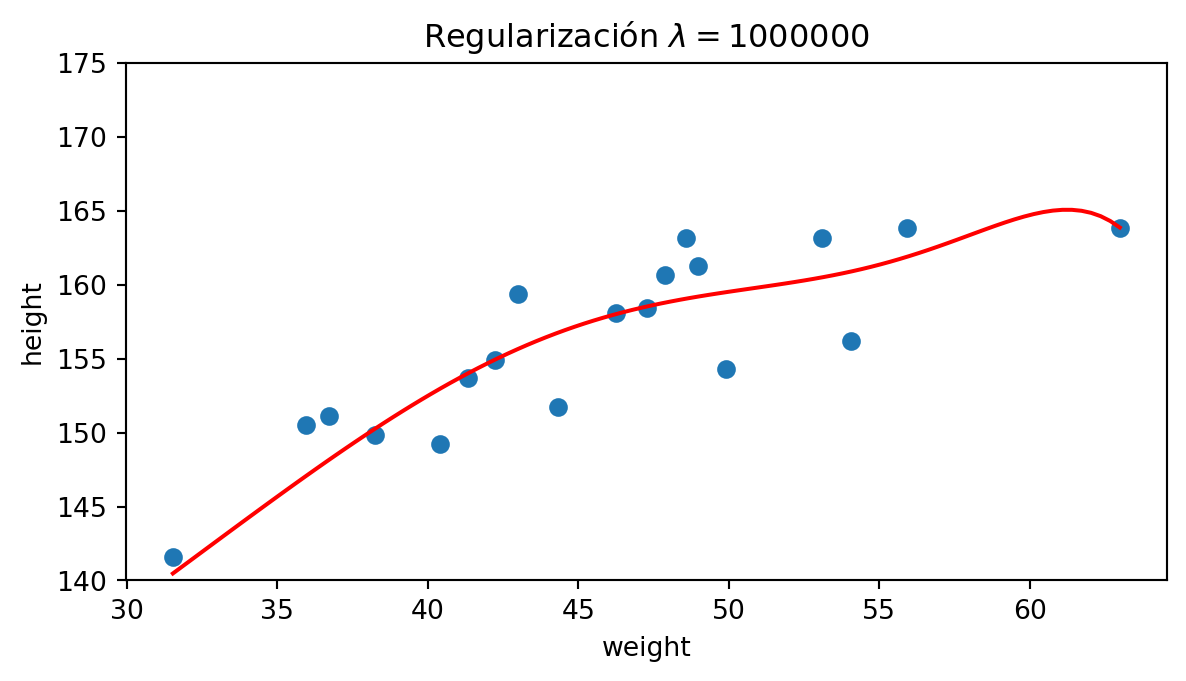
Modelos lineales regularizados: Lasso

En la regularización Lasso el término que se añade a la función de pérdidas es: \[ \mathcal{L}(\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - h(\theta) \rvert ^2 + \lambda \sum_{j=1}^k \theta_j \]

donde \(k\) es el grado del polinomio. Fíjate en que no se incluye el parámetro de bias \(\theta_0\) en la regularización.

Modelos lineales regularizados: Lasso

Seguimos utilizando un polinomio de grado 9:

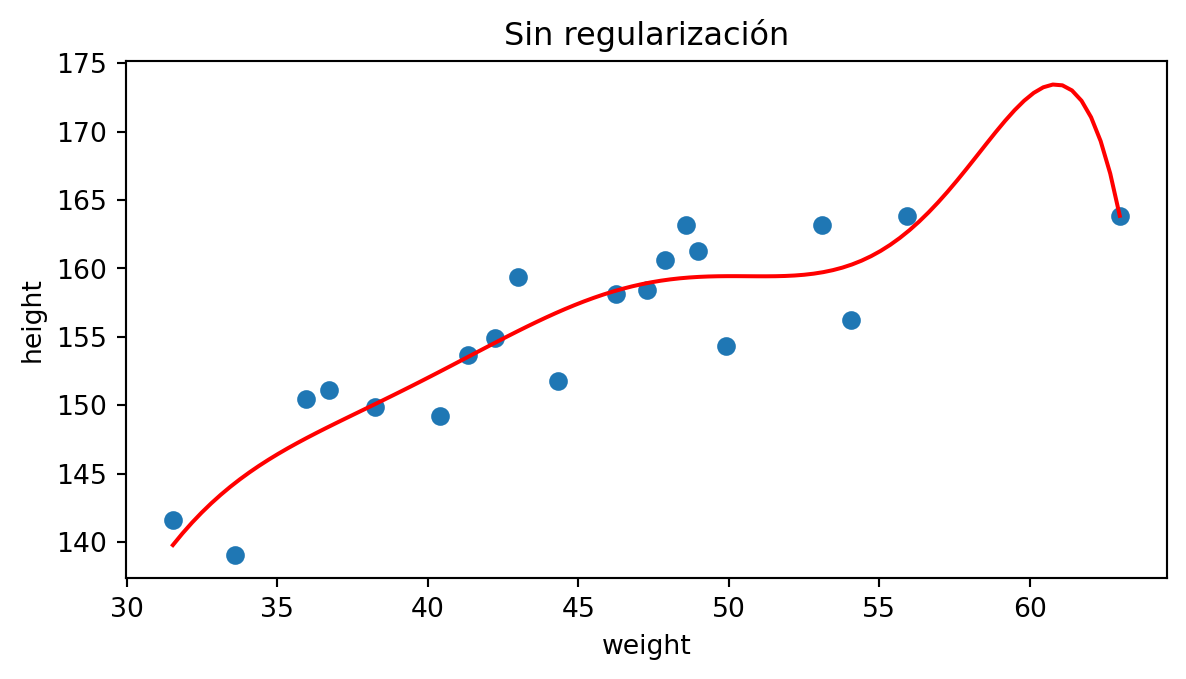
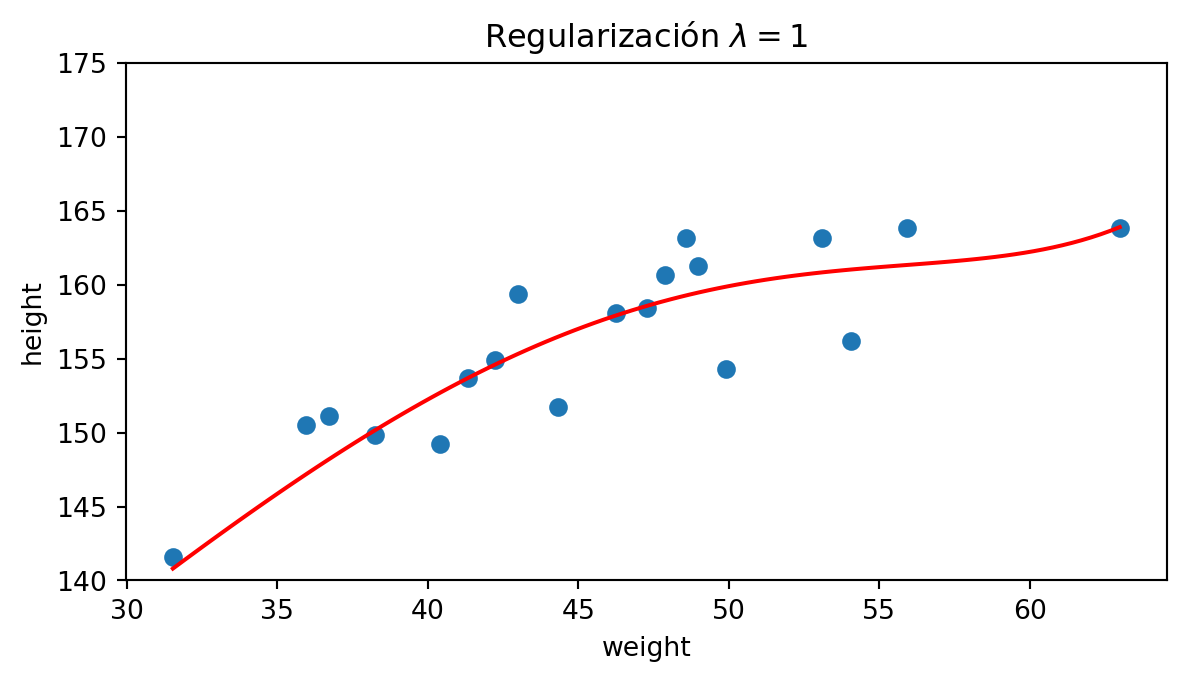
Modelos lineales regularizados: Elastic Net

La regularización Elastic Net es una combinación de las dos anteriores:

\[ \mathcal{L}(\mathbf{\theta}) = \frac{1}{N} \sum_{i=1}^N \lvert y_i - h(\theta) \rvert ^2 + r \lambda \theta^T\theta + (1-r) \lambda \sum_{j=1}^k \theta_j \]

donde el parámetro \(r\) da cuenta de la contribución de cada una de las regularizaciones. Si \(r=1\) sólo tenemos contribución de la regularización Ridge, y si \(r=0\) sólo tenemos contribución de la regularización Lasso.

Resumen

Resumen

• Hemos analizado con detalle la regresión lineal.
• Hemos ampliado la regresión lineal a múltiple.
• Hemos extendido la regresión lineal a modelos polinómicos.
• Hemos estudiado qué es la técnica de descenso del gradiente.
• Hemos introducido la regularización para mejorar el rendimiento.

Resumen

• Es importante que compruebes que se cumplen las condiciones para aplicar regresión lineal: residuos distribuido según una gaussiana centrada en el 0.