
Técnicas de entrenamiento de redes reuronales
Introducción
Aunque la redes neuronales parecen una estructura sencilla, se tardó tiempo hasta que se encontró el algoritmo que ajusta los pesos de la red para un conjunto de datos de entrenamiento.
De hecho, el resurgir de las redes neuronales vino de la mano del descubrimiento de cómo entrenarlas.
Sin embargo, incluso después de descubrir el algoritmo que permite entrenar redes neuronales, en la práctica, surgieron un buen número de problemas que dificultaban un entrenamiento eficiente.
Introducción
El entrenamiento de las redes neuronales es muy delicado, sobre todo, cuando tienen muchas capas.
Poco a poco se ha encontrado un serie de técnicas que hacen posible que se puedan entrenar las redes neuronales.
En esta presentación se muestran algunos de los problemas más comunes durante la fase de entrenamiento de una red neuronal profunda, y algunas de las técnicas más utilizadas para soslayar estos problemas.
Objetivos de aprendizaje
- Razonar el problema de la inicialización de los parámetros de una red neuronal.
- Decidir qué función de activación utilizar en función de sus características.
- Decidir qué optimizador utilizar basándose en las características de cada uno de ellos.
- Decidir si es necesario utilizar una estrategia de actualización de la tasa de aprendizaje y elegir la más adecuada.
Objetivos de aprendizaje
- Decidir si es necesario utilizar regularización.
- Elegir el tipo de capa más adecuada en cada caso.
Referencias
- Hands-on machine learning… Aurélien Géron.
- Deep Learning, Ian Goodfellow, Joshua Bengio and Aaron Courbille.
- Dive into deep learning, Aston Zhang et al.
Inicialización de parámetros
La importancia de la inicialización
La función de pérdidas de una red neuronal, en general, presenta múltiples extremos (mínimos y máximos).

La importancia de la inicialización
Como ya sabemos, para encontrar un mínimo utilizamos la técnica de descenso de gradiente, que depende del punto desde el que se inicie la búsqueda.
Además, la técnicas de retro propagación del gradiente es muy sensible a los valores de los pesos.
Todo ellos hace que sea complicado entrenar una red neuronal.
Afortunadamente, la investigación en redes neuronales ha permitido ir soslayando muchos de los problemas que presenta el entrenamiento.
Inizialización de Xavier Glorot y Yoshua Bengio
Xavier Glorot y Yoshua Bengio publicaron un trabajo donde presentaban sus conclusiones sobre la influencia de la inicialización de los pesos de una red neuronal.
Llegaron a la conclusión de que una buena estrategia es inicializar los pesos de cada capa de tal modo que sigan una distribución normal centrada en el origen y con desviación estándar:
\[\sigma^2 = \frac{1}{(input+output)/2}\]
Donde input es el número de conexiones de entrada en la capa, y out el número de conexiones de salida en la capa.
Inizialización de Xavier Glorot y Yoshua Bengio
Además, presentaron otra estrategia, una distribución uniforme entre
\[-\sqrt{3/(input+ountput)}, \sqrt{3/(input+ountput)}\]
Estas estrategias funcionan bien con las funciones de activación:
- tanh.
- sigmoide.
- softmax
Inizialización de Kaiming He
Kaiming He, por su parte, mostró que inicializar los pesos de la red con una distribución normal con
\[\sigma^2 = \frac{2}{(input+output)/2}\]
funciona bien cuando las funciones de activación son:
- ReLU.
- LeakyReLU.
- ELU, GELU, Swish, Mish.
Algunas de estas funciones de activación se presentan en la siguiente sección.
Show me the code
Si no se especifica lo contrario, Keras utiliza inicialización de Glorot.
Para cambiar la estrategia de inicialización podemos usar:
Si la inicialización es más sofisticada podemos utilizar :
Funciones de activación
Introducción
Como ya sabemos, si sólo sumamos las entradas de una red neuronal multiplicadas por un peso, la función que obtenemos a la salida sigue siendo lineal.
Las funciones de activación permiten tener salidas no lineales.
La función sigmoide fue muy utilizada al inicio de la investigación en redes neuronales profundas, pero, paulatinamente ha cedido el puesto a otras funciones de activación que han demostrado mejor comportamiento en la práctica.
Sigmoide
La función sigmoide ya la utilizamos cuando vimos regresión logística:
\[ sigmoide(x) = \frac{1}{1 + e^{-x}} \]
Es una función suave y derivable en todo \(\mathbb{R}\).
Tangente hiperbólica
La tangente hiperbólica es otra función comúnmente utilizada como función de activación:
\[ tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \]

También es una función suave y derivable en todo \(\mathbb{R}\).
ReLU
ReLU es el acrónimo de Rectified linear unit, con la siguiente definición:
\[ ReLU(x) = max(0, x) \\ = \frac{x + |x|}{2} \]
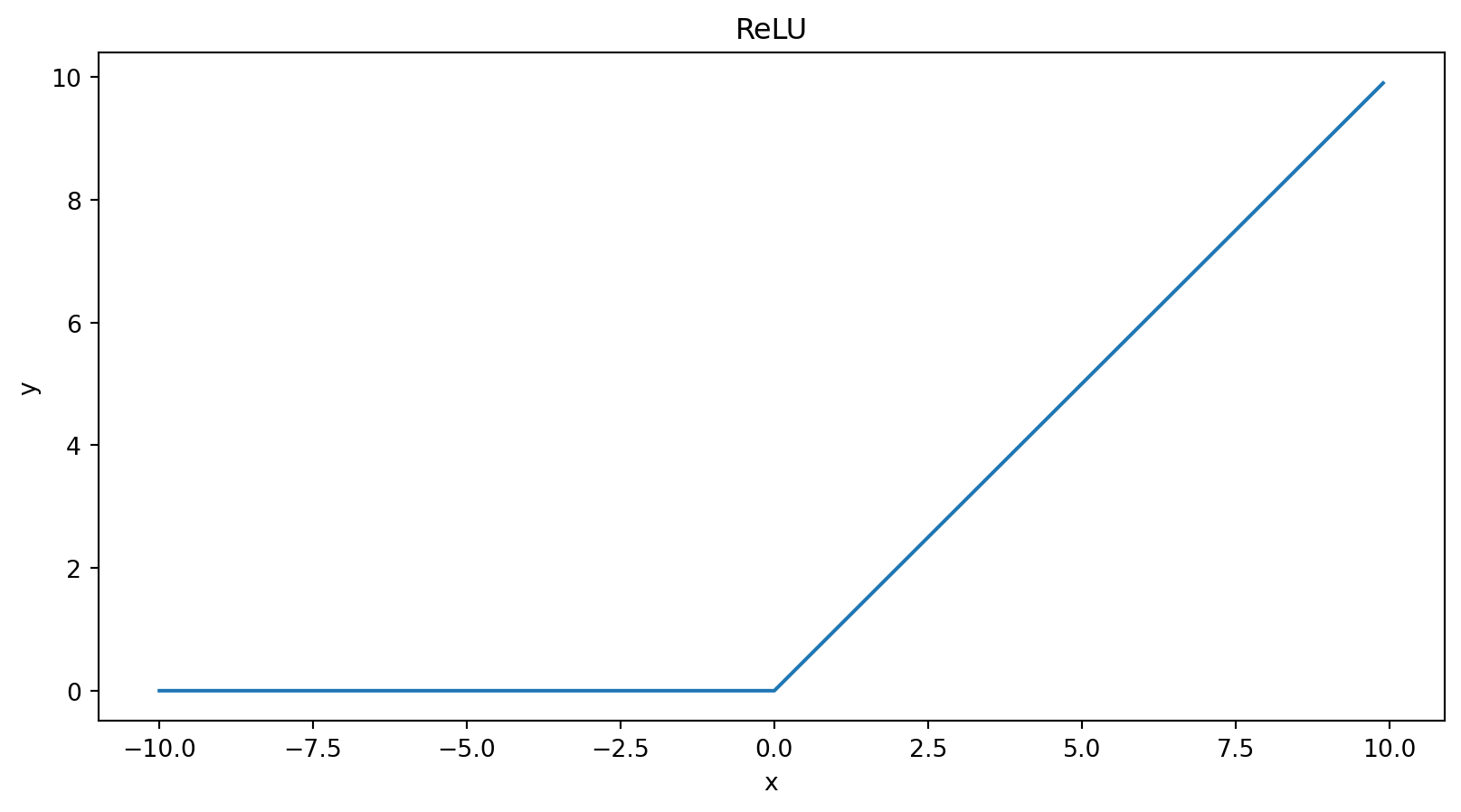
Que es derivable en todos los puntos excepto en el 0.
Leaky ReLU
Es una variante de ReLU:
\[ \begin{equation} Leaky ReLU(x) = \\ \begin{cases} x \quad \qquad if \quad x > 0, \\ 0.01x \quad if \quad x \leq 0 \end{cases} \end{equation} \]
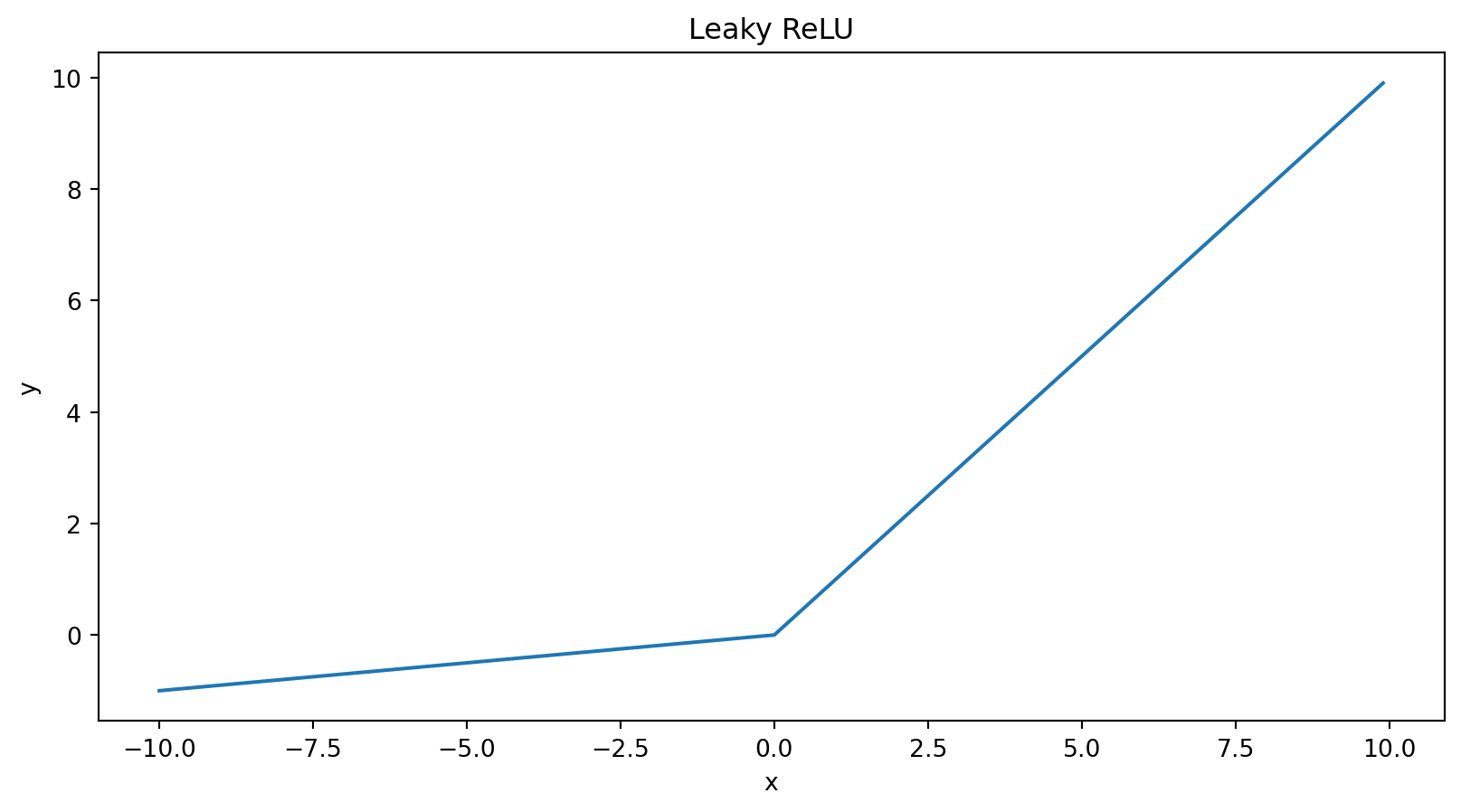
Evita que el gradiente decaiga rápidamente en la retro propagación.
Otras funciones de activación
Aún hay otras funciones de activación:
Swish: \(x \cdot sigmoide(x)\)
Softplus: \(ln(1 + e^x)\)
Mish: \(x \cdot tanh(softplus(x))\)
Y algunas más.
La función de activación tanh suele ser un buen principio. La función ReLU funciona muy bien en la mayoría de los casos.
Optimizadores
Introducción
En la presentación sobre regresión lineal vimos cómo utilizar la técnica de descenso de gradiente para encontrar el mínimo de la función de pérdidas:
\[ \theta^{i+1} = \theta^i - \eta \nabla_\theta \mathcal{L} \]
Esta técnica siempre funciona, pero a veces puede ser lenta es decir, se pueden necesitar muchos pasos para acercarnos al mínimo.
Introducción
Hay dos características que debemos tener en cuenta al seleccionar un optimizador:
- Rapidez de convergencia.
- Comportamiento de la convergencia.
Estas dos características son antagónicas los optimizadores con un buen comportamiento en la convergencia son, en general, lentos. Mientras que, por el contrario, los algoritmos rápidos no se suelen comportan tan bien en la convergencia.
Momentum
Han aparecido variación del descenso del gradiente (Boris Polyak) que necesitan un menor número de pasos para alcanzar el mínimo de la función de pérdidas.
\[ m^i = \beta m^{i-1} - \eta \nabla_\theta \mathcal{L} \\ \theta^{i+1} = \theta^i + m^{i} \]
El incremento tiene en cuenta el gradiente el gradiente en el paso anterior.
Un valor típico para \(\beta = 0.9\).
Nesterov Accelerated Gradient
La propuesta de Nesterov es calcular el gradiente no en el punto actual sino en un punto avanzado en la dirección del gradiente:
\[ m^i = \beta m^{i-1} - \eta \nabla_\theta \mathcal{L(\theta + \beta m^{i-1})} \\ \theta^{i+1} = \theta^i + m^{i} \]
Para que las expresiones sean más claras, a partir de este momento no voy a mostrar el índice de paso de actualización \(i\), en vez de ello, utilizaré el símbolo \(\leftarrow\) en vez de \(=\).
AdaGrad
Otro optimizador es AdaGrad que propone la siguiente actualización para los parámetros:
\[ s \leftarrow s + \nabla_\theta \mathcal{L(\theta)} \otimes \mathcal{L(\theta)} \\ \theta \leftarrow \theta - \eta \nabla_\theta \mathcal{L(\theta)} \oslash \sqrt{s + \epsilon} \]
Donde \(\otimes\) es el producto componente a componente de dos vectores, y \(\oslash\) es la división componente a componente.
Adam
Adaptative Moment Estimation (Adam) es otro optimizador ampliamente utilizado por sus buenos resultados.
\[ m \leftarrow \beta_1 m - (1 - \beta_1)\nabla_\theta \mathcal{L(\theta)} \\ s \leftarrow \beta_2 s + (1 - \beta_2) \nabla_\theta \mathcal{L(\theta)} \otimes \nabla_\theta \mathcal{L(\theta)} \\ \hat{m} \leftarrow \frac{m}{1 - \beta_1^t} \\ \hat{s} \leftarrow \frac{s}{1 - \beta_2^t} \\ \theta \leftarrow \theta + \eta \hat{m} \otimes \sqrt{\hat{s} + \epsilon} \]
Otros optimizadores
Aún existen otros optimizadores:
- RMSProp.
- AdaMax.
- Nadam.
- AdamW.
Todos ellos implementados en Keras.
Otros optimizadores
| Optimizador | Velocidad | Calidad convergencia |
|---|---|---|
| SGD | Lenta | Muy buena |
| Momentum | Media | Muy buena |
| Nesterov | Media | Muy buena |
| Adagrad | Alta | Para anticipadamente |
| RMSProp | Alta | Buena |
| Adam | Alta | Buena |
| AdaMax | Alta | Buena |
| Nadam | Alta | Buena |
| AdamW | Alta | Buena |
Extraído de Hands-on machine learning with TF…
Otros optimizadores
Esta página web es muy interesante para apreciar cómo varia el proceso de entrenamiento de una red con respecto de varios parámetros.
Aquí tienes un Google Colab para que pruebes a jugar con los parámetros de los distintos optimizadores.
Normalización por lotes
La normalización por lotes (Batch normalization) es otra técnica que intenta evitar el desvanecimiento/explosión del gradiente.
La idea es que antes (o después, según se mire) de una capa de la red neuronal, se añade otra capa que normaliza la entrada (o salida) de la capa para que estén centradas en cero y con \(\sigma^2 = 1\).
Para que durante el proceso de entrenamiento cada una de las capas de normalización calculen los estadísticos \(\mu\) y \(\sigma\), es necesario que lo haga sobre un subconjunto (batch) de los datos, de ahí el nombre de este tipo de capa.
Normalización por lotes
Este tipo de capa está implementado en Keras, y su uso es muy sencillo, simplemente se añade una de estas capas antes o después de otra capa, por ejemplo:
keras.layers.Dense(neuronas, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),Utilizaremos este tipo de capas cuando estudiemos las redes convolucionales.
Normalización por lotes
Las capas de normalización por lotes se pueden aplicar antes de la función de activación (a veces el entrenamiento funciona mejor).
Para ello, la técnica es no especificar ninguna función de activación en la capa (por ejemplo en una capa densa como en el ejempo), y se añade una capa de activación después de aplicar la normalización por lotes, como en este ejemplo:
keras.layers.Dense(neuronas, kernel_initializer="he_normal", use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),La capa densa (Dense) no usa ninguna función de activación; añadimos una capa de normalización por lotes (BathNormalization); y finalmente añadimos la capa con la función de activación (Activation) ReLU.
Recorte del gradiente
Otra técnica comúnmente utilizada para evitar la explosión del gradiente es, simplemente, limitarlo para que no sobrepase un cierto umbral (gradient clipping).
El recorte se activa al instanciar el optimizador, por ejemplo:
En este caso, después de calcular los gradiente de una capa, si alguno de ellos supera el umbral \(1.0\) se le asignará a ese gradiente en particular el valor este umbral.
Estrategias de actualización de la tasa de aprendizaje
Introducción
En la presentación de regresión lineal se presentó la técnica de descenso de gradiente. Recuerda que el término de la segunda derivada de la función de pérdidas lo sustituimos por un valor constante: la tasa de aprendizaje.
También vimos lo delicado que es la elección de su valor, si la tasa de aprendizaje es demasiado elevada puede que el algoritmo de descenso de gradiente nunca converja; o si la tasa de aprendizaje es demasiado pequeña puede que el descenso de gradiente necesite muchas iteraciones para alcanzar el mínimo.
Introducción
Muchas veces es más interesante definir una estrategia para ir adaptando el valor de la tasa de aprendizaje al avance del aprendizaje de manera que, si se puede avanzar rápidamente porque nos encontramos lejos de la solución, le asignamos un valor alto, y conforme nos acercamos al mínimo vamos disminuyendo la tasa para que el descenso de gradiente converja.
Y esta estrategia la podemos añadir de modo combinado con el optimizador.
Veamos algunos ejemplos.
Decaimiento en potencia
La actualización de la tasa de aprendizaje se hace según la siguiente expresión (donde \(\eta_0,s,c\) son hiperparámetros) : \[ \eta(t) = \frac{\eta_0}{(1 + epoca/s)^c} \]
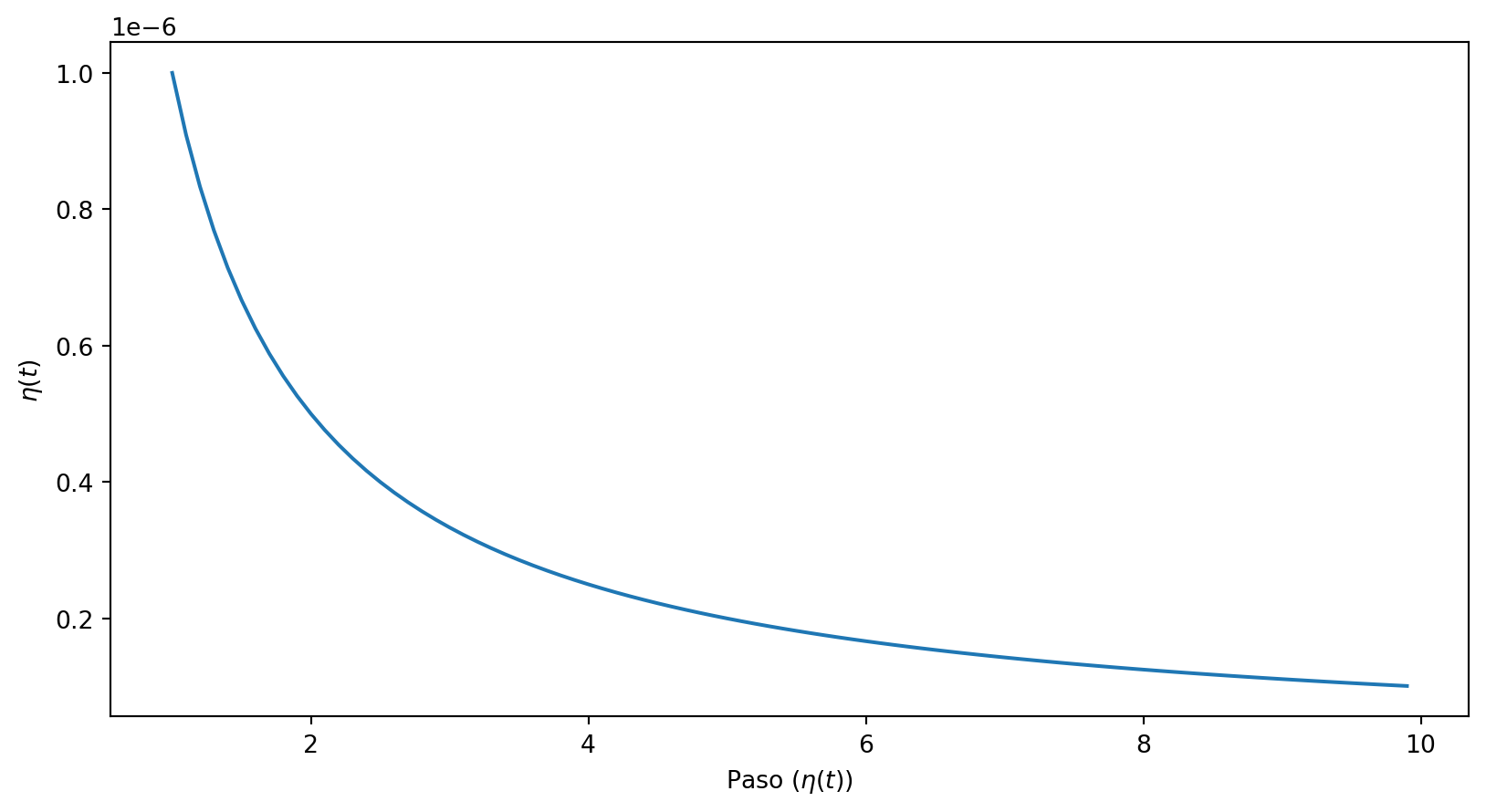
Decaimiento en potencia
En Python:
Donde decay es la inversa de \(s\).
\[ \eta(t) = \frac{\eta_0}{(1 + epoca/s)^c} \]
En este caso \(\eta_0 = 0.01\) y \(s = 10,000\).
Actualización de la tasa de aprendizaje propia
Si queremos definir nuestra propia función de actualización:
def mi_estrategia(epocas):
return 0.01/math.pow(1+ epoca/0.0001, 1)
estrategia = keras.callbacks.LearningRateScheduler(mi_estrategia)
model.fit(X, y, [resto de parámetros], callbacks=[estrategia])Pasamos al optimizador una función que devuelve la tasa de aprendizaje en función de la época.
Regularización
Introducción
Como ya sabemos, durante la fase de entrenamiento el modelo creado puede ajustar excesivamente los datos de entrenamiento (overftting), pero no trabajar tan bien con nuevos datos.
Para evitarlo, como ya hicimos en el caso de la regresión polinómica, empleamos la regularización.
Regularización \(l_1\) y \(l_2\)
En Keras añadir regularización a una capa es muy sencillo, simplemente se asigna un nuevo parámetro en el momento de creación de la capa.
Un ejemplo donde se usa regularización \(l_2\):
Dropout
Es una idea muy sencilla que suele mejorar el rendimiento de las redes neuronales y evitar el sobreajuste.
La idea es desactivar algunas neuronas, en toda la red.
En cada paso del entrenamiento, se selecciona un porcentaje de neuronas de la rede y se desactivan, es decir, se actúa como si no existiensen.
En el siguiente paso, se elige otro conjunto, se desactiva y se sigue adelante de este modo durante todo el entrenamiento de la red.
Dropout
Este tipo de capa está implementado en Keras, y su uso es muy sencillo:
keras.layers.Dense(neuronas, activation="relu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),En el caso anterior estamos indicando que se desactive el 20% de las neuronas de la red en cada uno de los pasos de entrenamieto.
Montecarlo dropout
Esta técnica no tiene ninguna capa asociada. La técnica consiste en clasificar la misma muestra un determinado número de veces, y hacer un promedio sobre los resultados obtenidos.
El truco consiste en que, para cada predicción, se desactiva un porcentaje de neuronas, tal y como se hace en la etapa de entrenamiento.
Montecarlo dropout
Supongamos que queremos hacer 100 predicciones, y en cada una de esas predicciones queremos congelar un porcentaje de las neuronas, para que no tomen parte en la predicción:
Finalmente promediamos sobre todas ellas:
El valor de cada predicción es el promedio de 100 predicciones, lo que suele tener más información en vez de basar el resultado en una única predicción.
Regularización Max-Norm
Otra técnica par evitar la explosión del gradiente es regularizar los pesos de entrada a las neuronas, de manera que el módulo de los pesos de las entradas no exceda una cierta cantidad. Esto se consigue activando un parámetro al instanciar la capa:
Tipos de capas
Introducción
Como ya hemos visto, Keras implementa muchas de las capas más utilizadas al construir redes neuronales.
En las siguientes presentaciones veremos algunas otras capas que tenemos disponibles en Keras.
Vamos a revisar las que hemos visto hasta ahora.
Capas densas
Una capa densa conecta la salida de una de sus neuronas con todas las neuronas de la siguiente capa.
Los parámetros comúnmente utilizados al instanciar este tipo de capa son:
- neuronas: el número de neuronas en la capa.
- activation: la función de activación a la salida de la capa.
- kernel_initializer: política de incialización de los pesos de la capa.
Capas de normalización por lotes
Este capa normaliza las entradas (o salidas) de la capa siguiente (o anterior).
Evita la explosión o desvanecimiento del gradiente.
Como puedes observar, no tiene argumentos.
Capas de activación
La función de activación de una capa se puede llevar a cabo en una capa de manera especializada
Es útil cuando se combina con otras capas, por ejemplo, tal y como hemos visto, con una capa de normalización por lotes:
keras.layers.Dense(neuronas, kernel_initializer="he_normal", use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),En este caso:
- Se lleva a cabo la normalización por lotes con la activación de la capa densa.
- Se aplica la función de activación sobre la salida normalizada.
Capas de Dropout
Desactivan un porcentaje de neuronas durante la fase de entrenamiento:
El argumento es la fracción de neuronas que se desactivan.
Como hemos visto, la técnica de dropout se puede combinar con la técnica de Montecarlo para hacer predicciones más informadas.
Resumen
Resumen
Entrenar una red neuronal es una tarea técnicamente compleja.
Los principales problemas con los que nos encontramos son:
- Inicializar los parámetros de la red.
- Controlar el desvanecimiento/explosión del gradiente.
- Reducir el tiempo de entrenamiento.
- Sobreajustar los datos de entrenamiento.
Resumen
La investigación en redes neuronales ha ido solucionando cada uno de estos problemas:
- Evitar inicializar los parámetros de la red de forma aleaotoria.
- Utilizar normalización por lotes.
- Utilizar funciones de activación alternativas a la función sigmoide y tangente hiperbólica.
- Utilizar mejores optimizadores que el descenso estocástico de gradiente.
- Utilizar regularización dropout.
Resumen
Es importante que aprecies que muchos de los resultados y técnicas que hemos visto son muy recientes.
La investigación en redes neuronales es un tema de gran actualidad.
Los resultados en este campo en los próximos años prometen ser espectaculares.
Recursos

Aprendizaje Automático (IR2130) - Óscar Belmonte Fernández