Redes neuronales recurrentes
Objetivos de aprendizaje
- Definir qué es una serie temporal, su componente de tendencia y su componente de estacionalidad.
- Comparar las redes convolucionales con las redes recurrentes.
- Construir una red recurrente (profunda) para la predicción de series temporales.
- Construir una red LSTM (profunda) para la predicción de series temporales.
- Relacionar las redes recurrentes y LSTM con otros modelos de aprendizaje.
Introducción
Introducción
La dependencia entre los elementos de una secuencia es una característica que podemos encontrar en muchos conjuntos de datos.
Algunos ejemplo son:
- El nivel de CO2 en un determinado punto depende del nivel de CO2 en el mismo punto en un instante anterior.
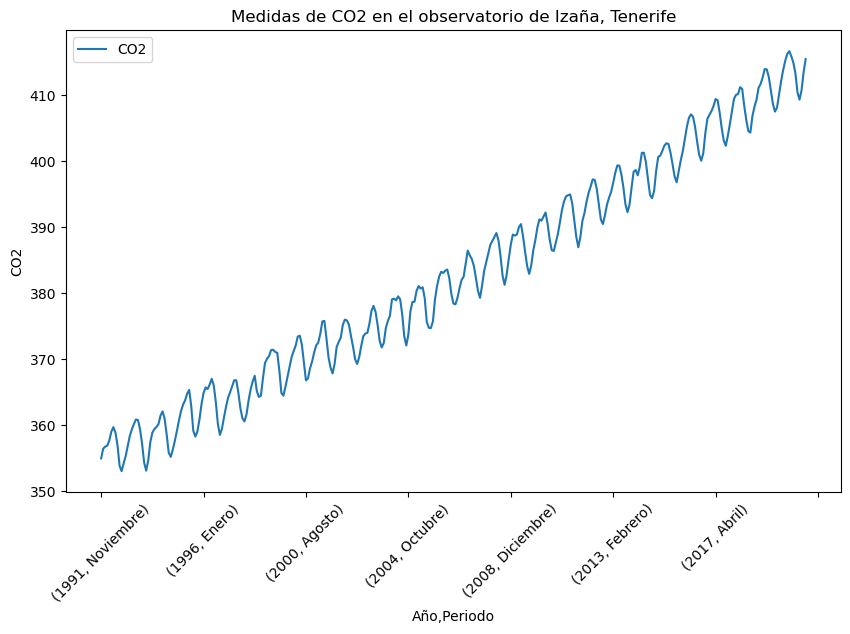
Introducción
- La temperatura ambiente en un determinado punto depende de la temperatura en el mismo punto en un instante anterior.
- La cotización de un valor en bolsa en un día depende de su valor en el día anterior.
- La presión arterial de un paciente en un instante depende de su presión arterial en el instante anterior.
En todos estos casos la secuencia de datos es temporal, pero no es la única posibilidad.
Introducción
Otros ejemplos donde no existe (explicitamente) componente temporal son:
- La siguiente letra dentro de una frase depende la secuencia de letras anteriores.
- La siguiente imagen en un vídeo depende de la secuencia anterior de imágenes.
- Para traducir una palabra entre dos lenguas necesitamos todas las letras de la palabra.
- La traducción de un texto entre dos lenguas se hace frase a frase.
Series temporales
Series temporales
Una serie temporal de datos es una secuencia de datos con un orden temporal.
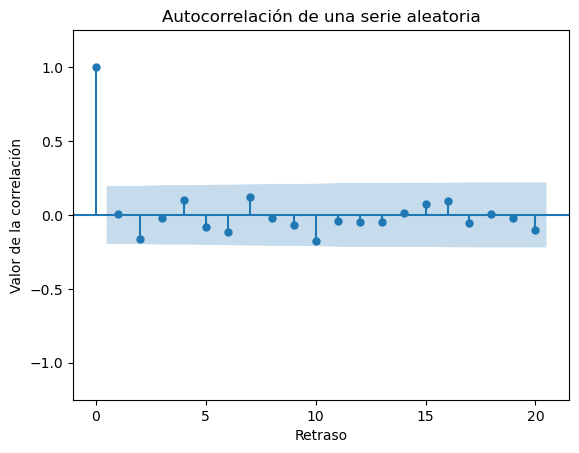
Autocorrelación
Muchas veces ocurre que los datos en una serie temporal están auto-correlacionados, existe una correlación entre los datos y los mismos datos retrasados, o adelantados en el tiempo.
Dicho de otro modo, la autocorrelación es la correlación de los datos con ellos mismos.
En Python:
Donde i indica cuanto se desplaza la señal al calcular la correlación.
Autocorrelación
Los diagramas de autocorrelación es una manera gráfica de mostrar la dependencia temporal de los datos.

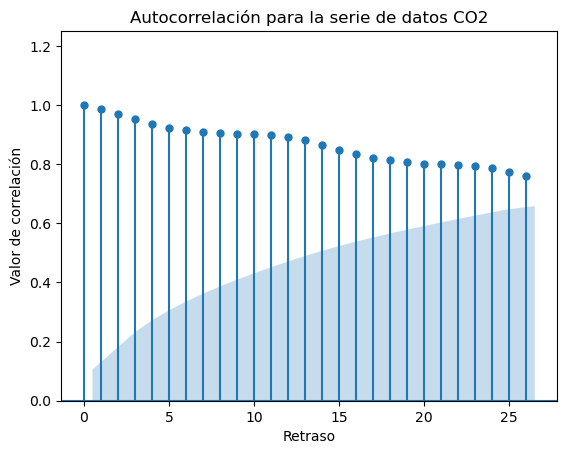
Autocorrelación
Los diagramas de autocorrelación es una manera gráfica de mostrar la dependencia temporal de los datos.
Tendencia y estacionalidad
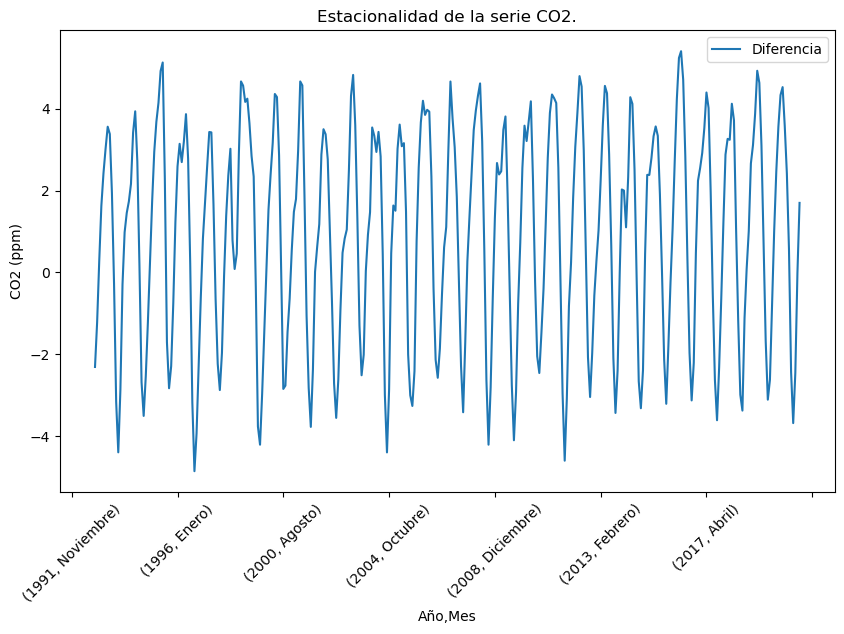
A veces, en las series temporales, se puede observar una componente de tendencia y sobre ella una componente estacional.

Tendencia y estacionalidad
A veces, en las series temporales, se puede observar una componente de tendencia y sobre ella una componente estacional.
Show me the code
Calcular la media de una serie de datos con una ventana deslizante es muy sencillo en Python:
Donde 12 indica el número de muestras que se tomarán en la ventana deslizante.
Vamos a ver un nuevo tipo de redes neuronales que pueden hacer predicciones sobre series temporales.
Objetivo de las RNN
Objetivo de las RNN
El objetivo de las redes neuronales recurrentes es dar una salida a partir de una entrada, pero, al contrario que en el caso de las redes convolucionales, el tamaño de la entrada puede ser cualquiera, no es fijo.
Rcuerda que al trabajar con redes convolucionales todas las imágenes deben tener el mismo tamaño ancho x alto.
Arquitectura de las RNN
Secuencias y vectores
Vamos a definir una secuencia como un conjunto ordenado con un número de elementos no determinado, podemos tener secuencias de un único elemento o de muchos elementos. Por ejemplo una secuencia temporal de datos puede tener cualquier tamaño, una frase puede tener cualquier número de letras.
Los vectores los vamos a definir como un conjunto ordenado con un número de elementos fijo. Por ejemplo cuando clasificamos imágenes con una red convolucional, todas ellas tienen el mismo tamaño.
Secuencias y vectores
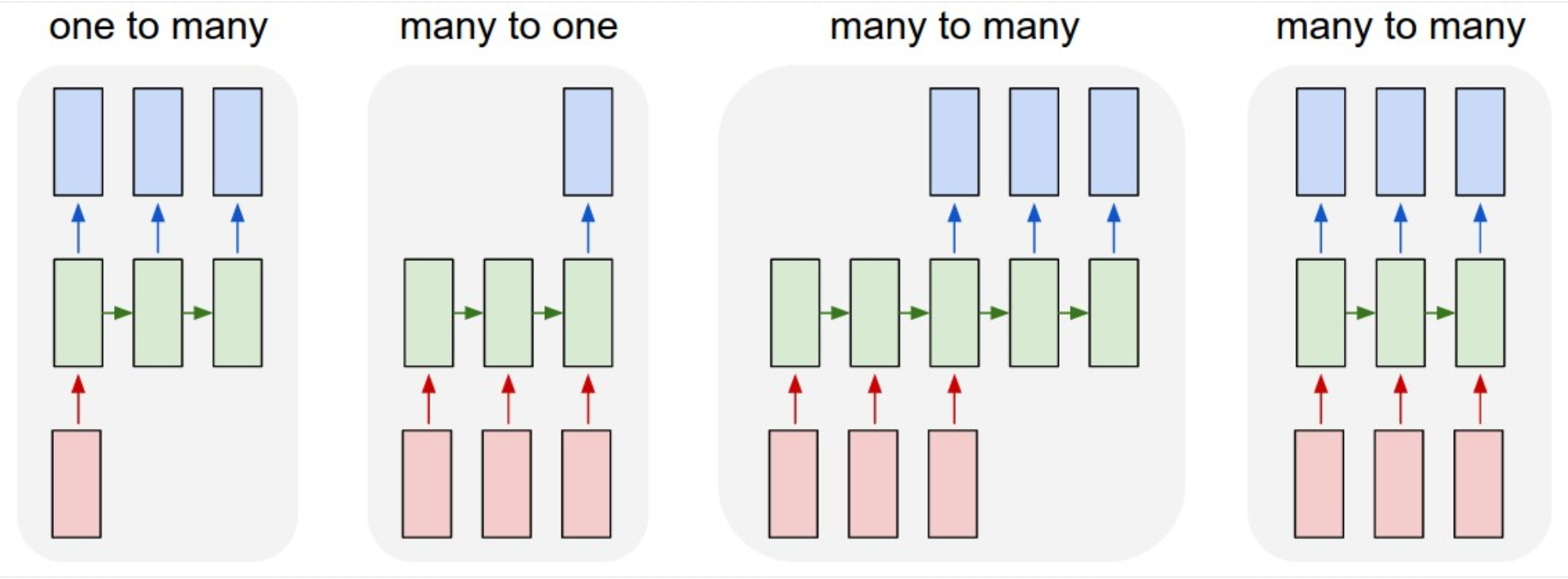
En este gráfico se muestran todas las combinaciones posible a la entrada y a la salida:
Secuencias y vectores
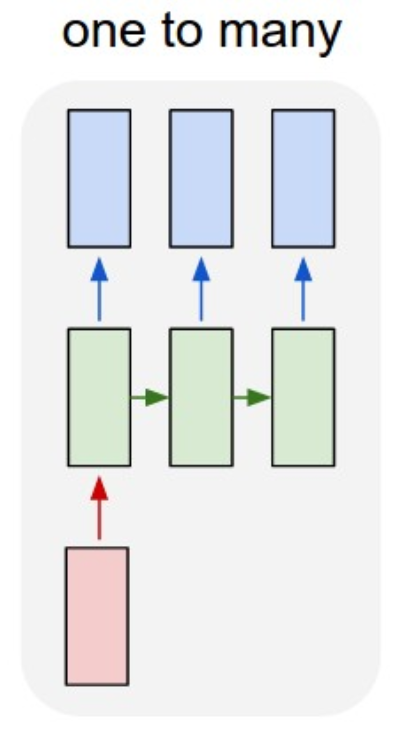
Este caso es una transformación de vector a secuencia. Un ejemplo es pasar a la red una imagen (vector), y que la red nos devuelva una descripción de lo que se ve en la imagen.
Secuencias y vectores
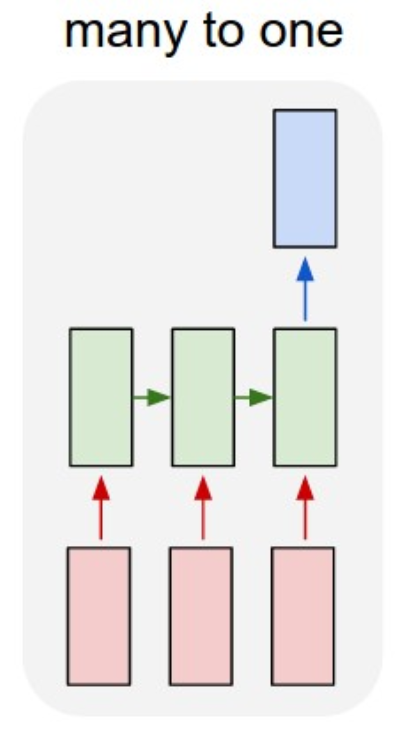
En este caso se le pasa una secuencia a la red y esta debe proporcionar un único valor a la salida. Por ejemplo, pasamos un texto a la red, y la red nos debe indicar si el texto contiene sesgos sexistas.
Secuencias y vectores
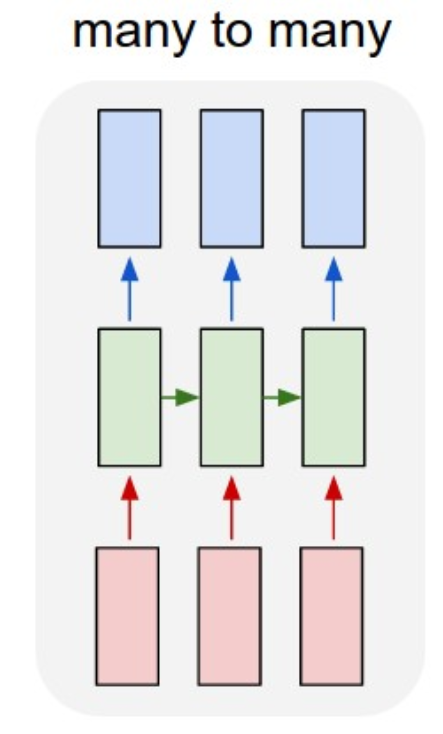
Este caso es una transformación de secuencia a secuencia. Por ejemplo, proporcionamos un texto en una lengua a la red y la red debe traducir el texto a otra lengua.
Secuencias y vectores
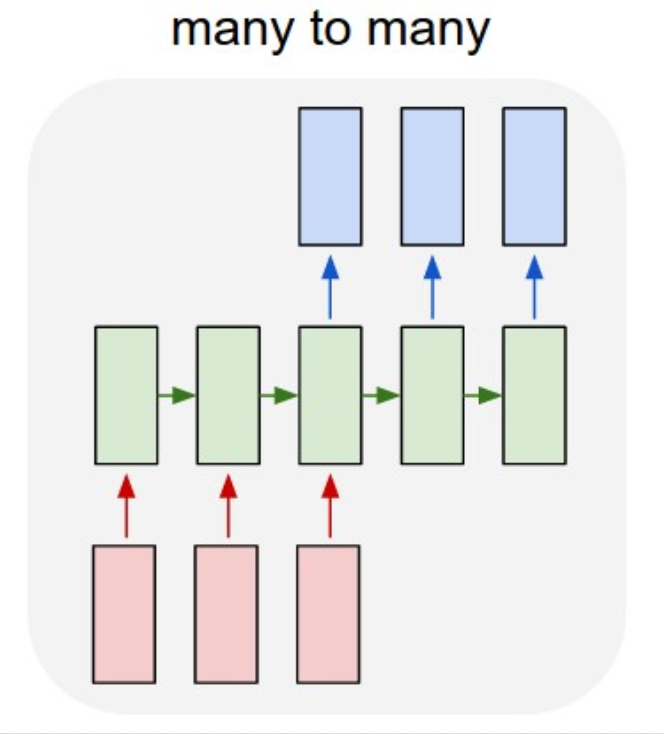
Es una extensión del caso de vector a secuencia. Por ejemplo, presentamos una secuencia de imágenes a la red, y esta debe generar un texto para cada una de ellas. Imagina, por ejemplo, la interpretación de una película para personas sordas.
Arquitectura de las RNN
La idea básica de las redes recurrentes es que cada neurona almacena un estado \(h_t\) que se calcula a partir de la entrada \(x_t\) y el estado anterior \(h_{t-1}\)
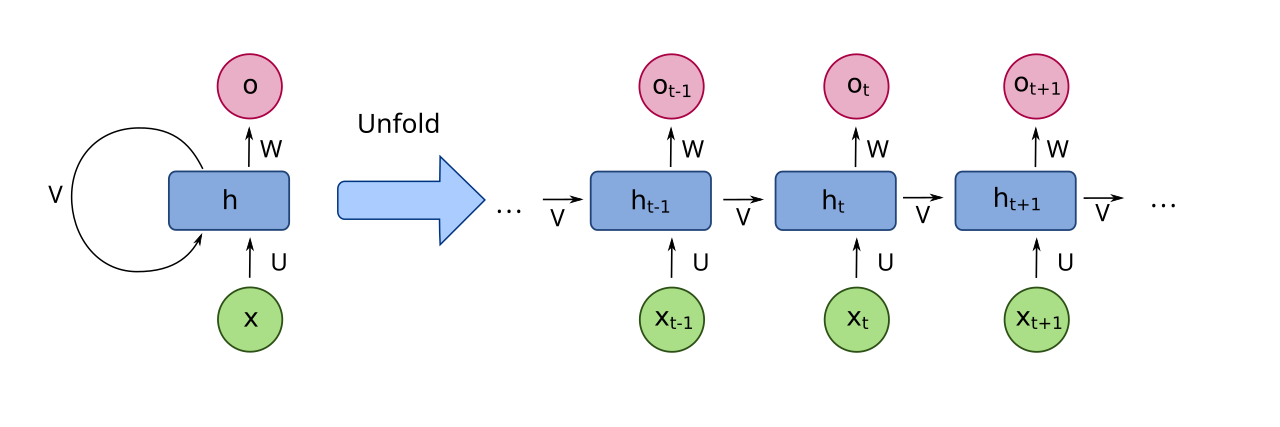
Arquitectura de las RNN
Este es el despliegue de la rede recurrente a lo largo del tiempo.
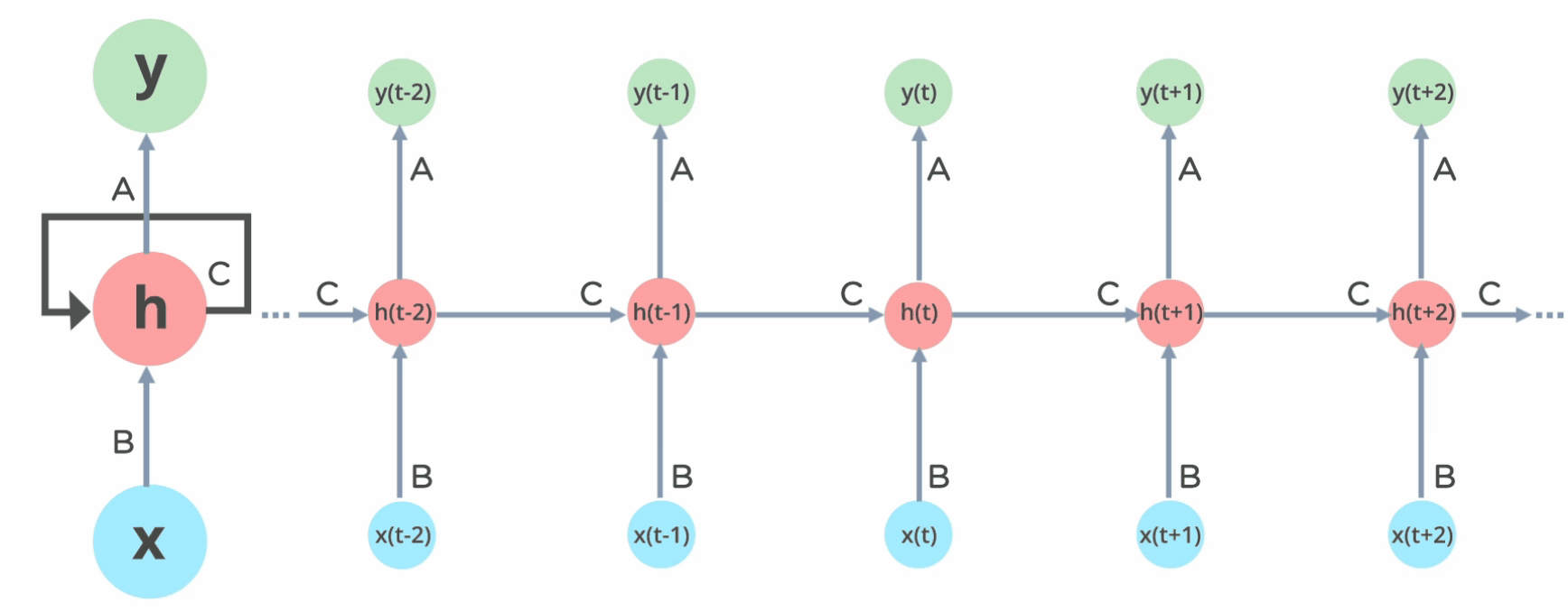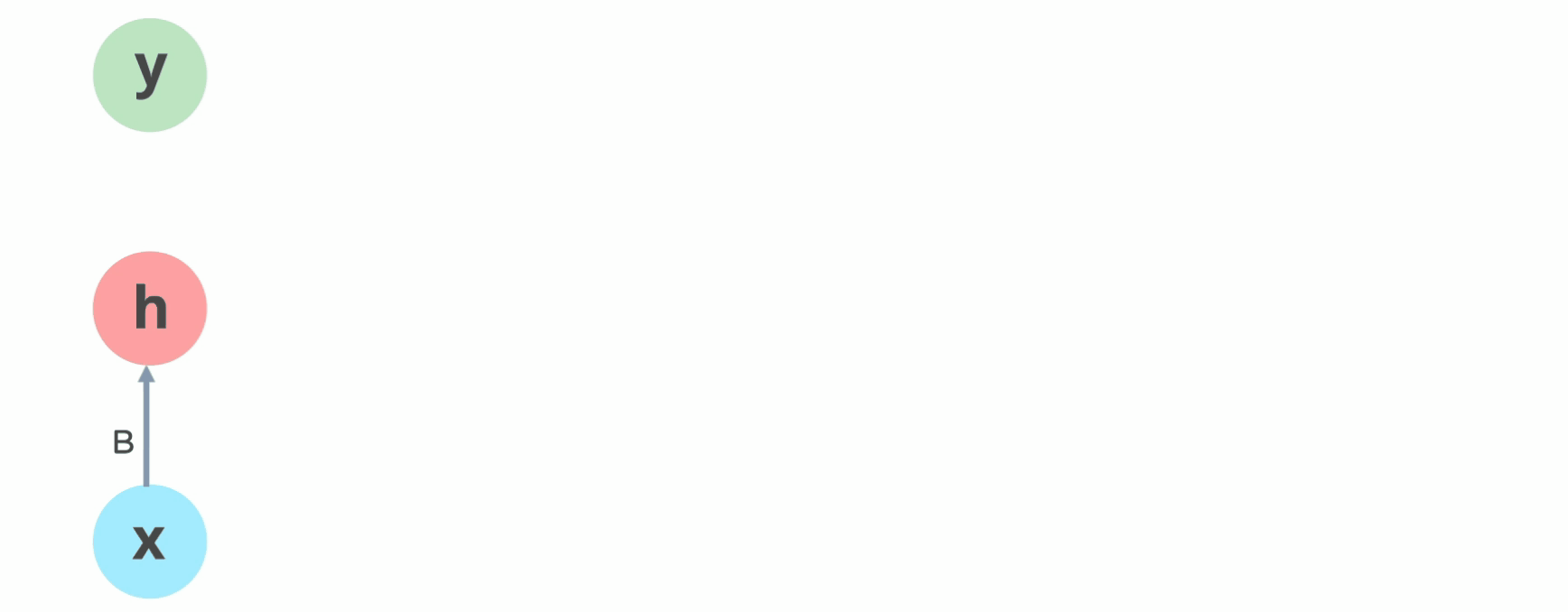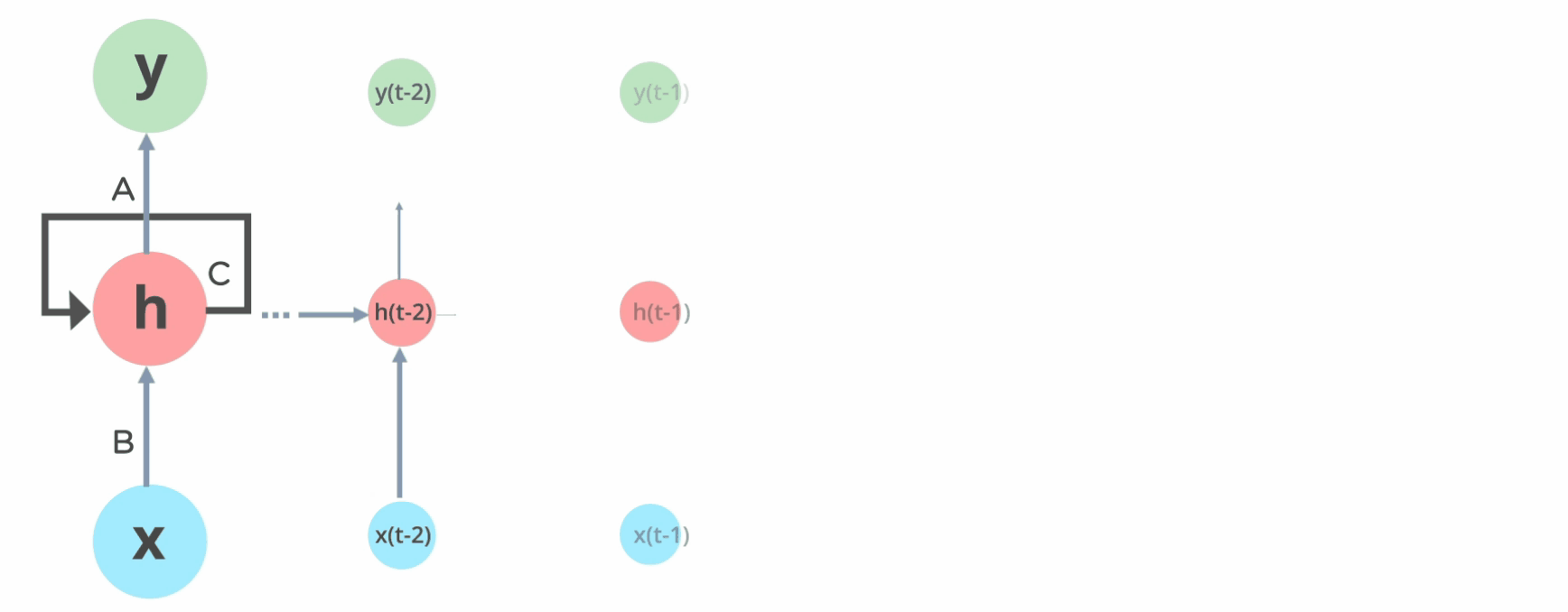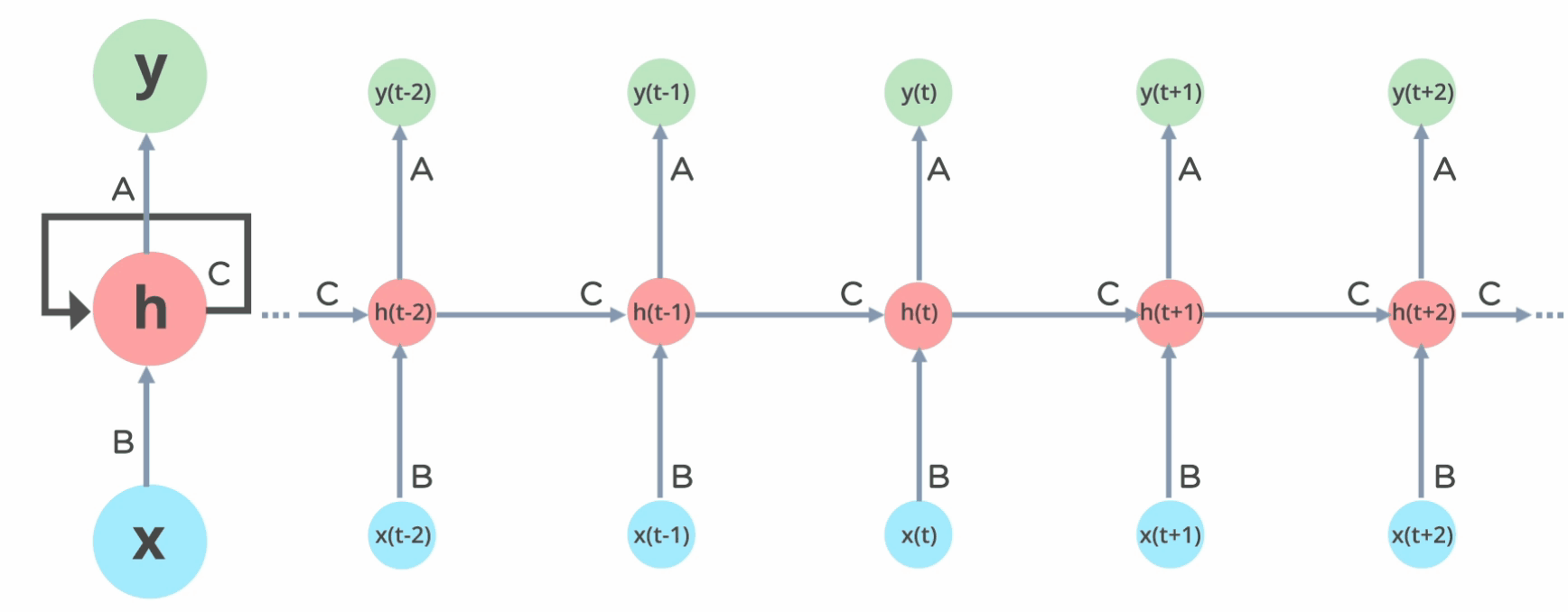
Arquitectura de las RNN
La salida en \(y_t\) se calcula en función del estado oculto \(h_{t}\):
\[ y_t = f(W_{yh} h_t + b_y) \]
El estado oculto \(h_t\) se calcula en función de la entrada \(x_t\) y del estado oculto anterior \(h_{t-1}\):
\[ h_t = f(W_{hh} h_{t-1} + W_{hx} x_t + b_h) \]
El estado oculto es la memoria de la neurona.
Arquitectura de las RNN
En el proceso de entrenamiento, se ajustan tanto los pesos de la matriz que calcula la salid \(y_t\) como los pesos de las matrices que calculan el estado oculto \(h_t\).
Veamos como definir y entrenar redes recurrentes.
Show me the code
Como ejemplo, vamos a trabajar con la serie de datos temporales de concentración de CO2 para intentar predecir su evolución a un periodo de meses en el futuro.
La primera tarea es decidir qué tipo de red recurrente vamos a implementar:
- One to many.
- Many to one.
- Many to Many.
En nuestro caso, a partir de una serie temporal de datos, queremos predecir cuál es el siguiente dato. Por lo tanto tenemos una estructura many to one.
Show me the code
El objetivo es, a partir de una serie de 10 datos, predecir el siguiente valor en la serie.
Vamos a empezar escalando los datos:
Cada entrada de entrenamiento es una serie de 10 elementos de la serie temporal, la salida es el siguiente dato en la serie:
[[0.03046482 0.05354899 0.05841709 0.06092965 0.07333543 0.09422111
0.1048995 0.09170854 0.06171482 0.01303392]] --> 0.0
[[0.05354899 0.05841709 0.06092965 0.07333543 0.09422111 0.1048995
0.09170854 0.06171482 0.01303392 0. ]] --> 0.018844221105527303
[[0.05841709 0.06092965 0.07333543 0.09422111 0.1048995 0.09170854
0.06171482 0.01303392 0. 0.01884422]] --> 0.03643216080402034Show me the code
Ahora ya podemos construir la red, vamos a empezar con una red sencilla de una única capa:
modelo = Sequential([
Input(shape=(1, 10)), # Cada entrada es un vector columna de 10 elementos.
SimpleRNN(64), # 64 neuronas recurrentes.
Dense(1) # Un único valor a la salida, la predicción.
])La entrenamos:
Show me the code
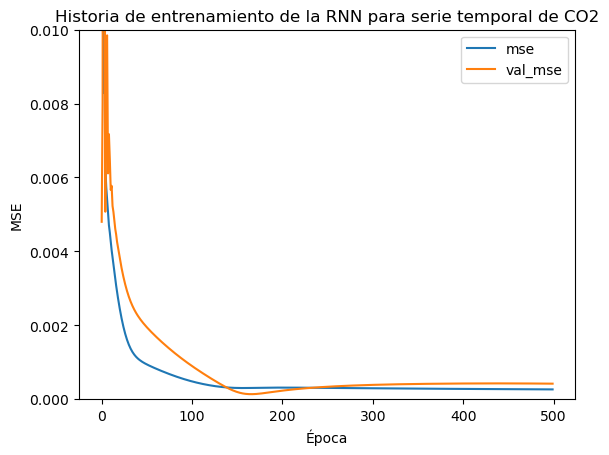
Prácticamente no existe sobreentrenamiento.
Show me the code
Hacemos las predicciones:
y_pred = modelo.predict(X_test)
print(y_pred)
y_pred = scaler.inverse_transform(y_pred)
y_test = y_test.reshape(-1, 1)
y_test = scaler.inverse_transform(y_test)Fíjate en que debemos deshacer el escalado.
Show me the code
Y este es el resultado que obtenemos:
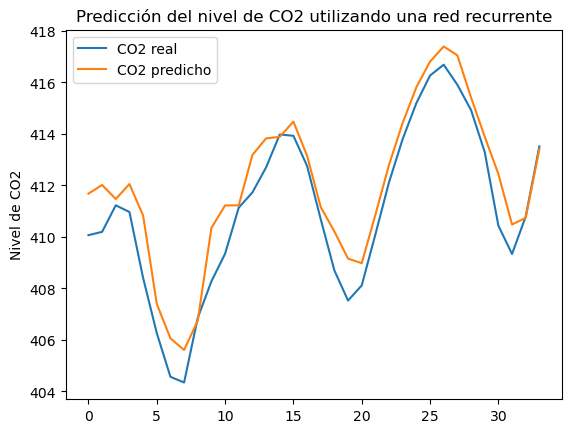
MSE: 1.34
Show me the code
Para definir una red recurrente profunda, debemos pasar de una capa a otra la secuencia generada:
modelo = Sequential([
Input(shape=(1, steps)),
SimpleRNN(128, return_sequences=True),
SimpleRNN(64, return_sequences=True),
SimpleRNN(32),
Dense(1)
])Fíjate en el segundo argumento de las primeras capas recurrentes.
Show me the code
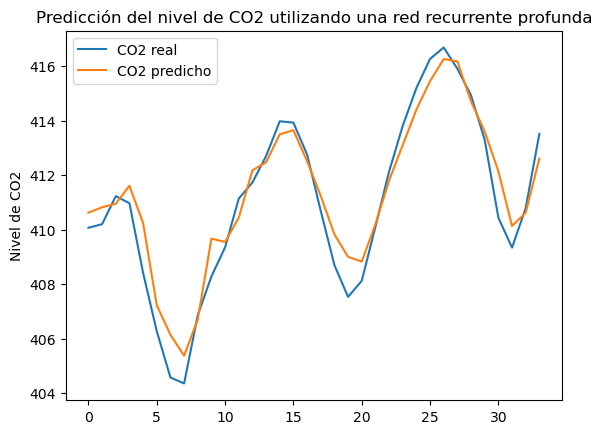
MSE: 0.67. El error cuadrático medio ha mejorado.
Redes Long Short Term Memory - LSTM
El problema del desvanecimiento
Si las secuencias que utilizamos en el entrenamiento son largas, la contribución de los primeros términos se desvanece:
\[ y_t = g(\_,h_t,\_) \\ h_t = f(\_,h_{t-1},\_) \rightarrow y_t = g(f(\_,h_{t-1},\_)) \\ h_{t-1} = f(\_,h_{t-2},\_) \rightarrow y_t = g(f(f(\_,h_{t-2},\_))) \\ h_{t-2} = f(\_,h_{t-3},\_) \rightarrow y_t = g(f(f(f(\_,h_{t-3},\_)))) \\ \]
El término \(g(f(f(f(\_,h_{t-3},\_))))\) se va haciendo pequeño. La contribución de los primeros valores de la serie tienen una contribución baja.
Arquitectura de la redes LSTM
La solución de las redes LSTM es añadir, dentro de cada neurona, un conjunto de puertas lógicas que añaden memoria a largo plazo.
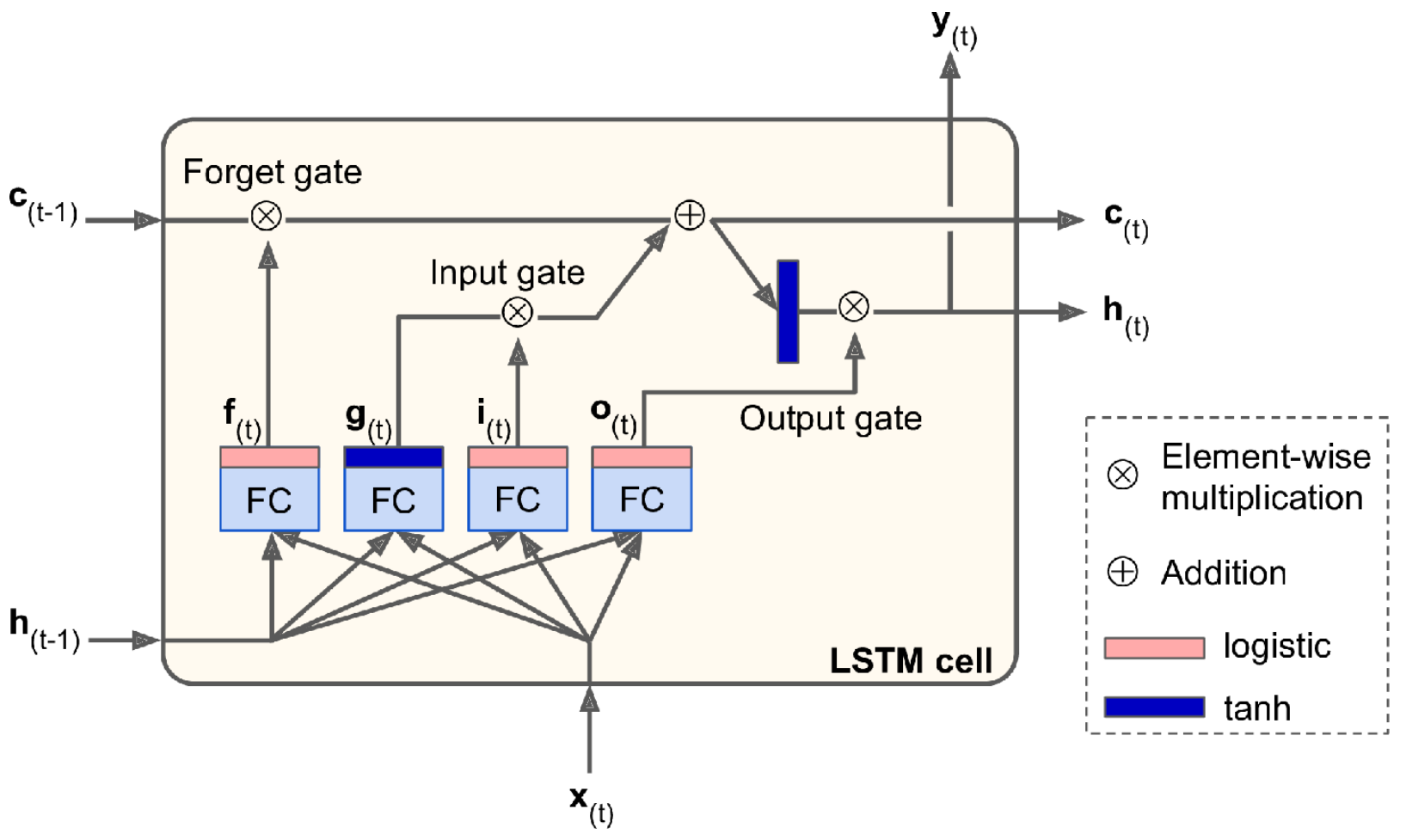
Fuente: Hands-on machine learning… Aurélien Géron.
Arquitectura de la redes LSTM

forget gate: controla qué parte de memoria se borra.
input gate: controla qué parte de \(g(x)\) debe añadirse a la memoria.
output gate: controla la parte de la memoria que se utiliza para calcular la salida y el estado oculto.
Arquitectura de la redes LSTM
Las funciones \(f,g,i,o\) dependen tanto del estado oculto \(h_t\) como de la entrada \(x_t\).
\[ i_t = \sigma(W_{ih} h_{t-1} + W_{ix} x_t + b_i) \\ f_t = \sigma(W_{fh} h_{t-1} + W_{fx} x_t + b_f) \\ o_t = \sigma(W_{oh} h_{t-1} + W_{ox} x_t + b_o) \\ g_t = tanh(W_{gh} h_{t-1} + W_{gx} x_t + b_g) \\ \]
Las puertas combinan estos resultados para guardar el estado a largo plazo.
Show me the code
Desde el punto de vista de la programación con Tensorflow sólo tenemos que cambiar el nombre de la capa:
Hemos sustituido la capa recurrente por la LSTM.
Show me the code
El resultado de la predicción:
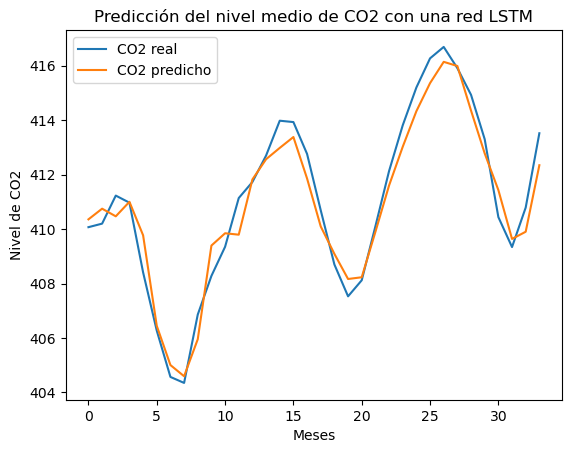
MSE: 0.52
Show me the code
La historia del entrenamiento:
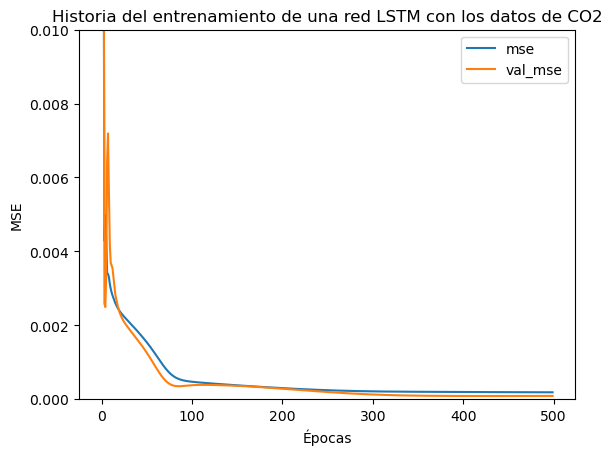
Show me the code
Si comparamos los resultados de la red recurrente con la red LSTM:
 RME: 1.34
RME: 1.34
 RME: 0.52
RME: 0.52
Con el mismo número de neuronas, la red LSTM funciona mejor en este caso.
Show me the code
Definir una red LSTM profunda es, de nuevo, sustituir el tipo de capa.
modelo = Sequential([
Input(shape=(1, steps)),
LSTM(128, return_sequences=True),
LSTM(64, return_sequences=True),
LSTM(32),
Dense(1)
])De nuevo, fíjate en el uso del parámetro return_sequences=True en las primeras capas de la red.
Show me the code
El resultado:
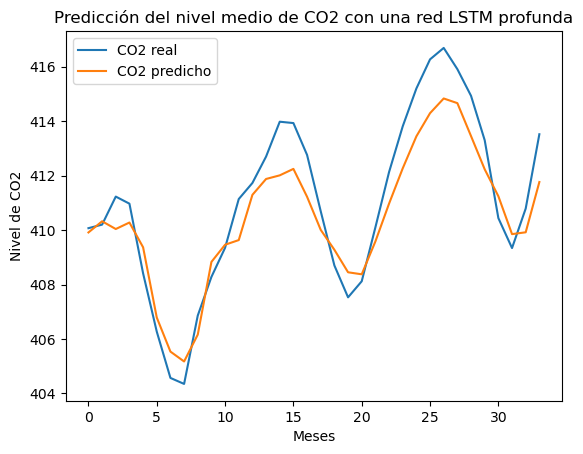
RME: 1.28 el resultado ha empeorado, para este caso particular.
Alternativas al estudio de series temporales
ARMA y sus derivadas
El modelo Autoregresive Moving Average (ARMA) predice el próximo valor en una serie temporal a partir de los valores actuales y las diferencias entre los valores reales y los predichos anteriormente:
\[ \hat y_t = \sum_{i=1}^p \alpha_i y_{t-i} + \sum_{i=1}^q \theta_i \epsilon_{t-i} \\ \epsilon_{t-1} = y_{t-1} - \hat y_{t-1} \\ \]
ARMA y sus derivadas
En este caso, el entrenamiento consiste en encontrar los mejores valores para los parámetros \(\alpha_i\) y \(\theta_i\) para una secuencia temporal dada, y unos hiperparámetros \(p\) y \(q\).
Es importante notar que este modelo asume la estacionalidad de la serie. No podríamos aplicar este modelo a la serie de datos de CO2, pero sí a su componente estacional.
ARMA y sus derivadas
El modelo Autoregresive Integrated Moving Averange (ARIMA) permite trabajar con series no estacionarias.
La idea básica de este modelo es que en el cálculo de la predicción también se introduce una media deslizante sobre los datos de la serie para eliminar la posible componente de tendencia de la serie.
Algo parecido a lo que hemos hecho ad-hoc con la serie de datos de concentración de CO2
Existen otras versiones que intentan introducir mejoras sobre los modelos anteriores, como es el caso de SARIMA.
Cadenas de Markov
Las cadenas de Markov son un modelo que predice el siguiente valor en una secuencia temporal. No es necesario que los valores sean numéricos, pueden ser de cualquier tipo.
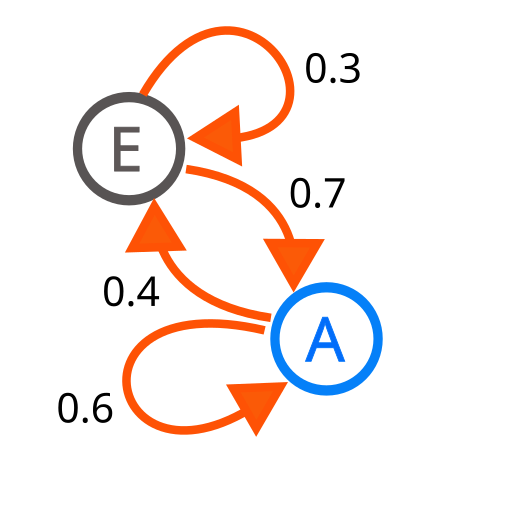
A y E son los dos estados. Las flechas indican la probabilidad de las transiciones entre estados.
Cadenas de Markov
Las transiciones se pueden representar como una matriz:

\[ \begin{matrix} & A & E \\ A & 0.6 & 0.7 \\ E & 0.4 & 0.3 \\ \end{matrix} \]
Cadenas de Markov
Las probabilidades de los estados finales se calculan multiplicando la matriz de transición por el vector de estado:
\[ \begin{bmatrix} 0.6 & 0.7 \\ 0.4 & 0.3 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} 0.6 \\ 0.4 \\ \end{bmatrix} \]
Es decir, si partimos del estado A, el siguiente estado será A con un 60% de probabilidad y B con un 40% de probabilidad.
Si queremos la probabilidad en el segundo instante, hacemos:
\[ \begin{bmatrix} 0.6 & 0.7 \\ 0.4 & 0.3 \\ \end{bmatrix} \begin{bmatrix} 0.6 & 0.7 \\ 0.4 & 0.3 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} 0.639 \\ 0.361 \\ \end{bmatrix} \]
Cadenas de Markov
Este tipo de matrices, cada una de sus columnas suman 1, tienen algunas propiedades interesantes, una de ellas es la de tener un estado estacionario.
Si multiplicamos infinitas veces a matriz por cualquier estado inicial de partida, llegamos a un estado que no varia, el estado estacionario.
\[ \begin{bmatrix} 0.6 & 0.7 \\ 0.4 & 0.3 \\ \end{bmatrix}^\infty \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} 0.\widehat{63} \\ 0.\widehat{36} \\ \end{bmatrix} \]
Cadenas de Markov
Dicho de otro modo, el vector \(\begin{bmatrix} 0.\widehat{63} \\ 0.\widehat{36} \\ \end{bmatrix}\) es autovector de la matriz con autovalor \(\lambda=1\).
Entrenar un modelo de cadena de Markov implica estimar la matriz de transición dada una cadena.
Modelos ocultos de Markov
En los modelo ocultos de Markov, no se conoce el estado en el que se encuentra el sistema, de ahí lo de ocultos, sólo se ven las observaciones que se emiten en cada uno de los estados.
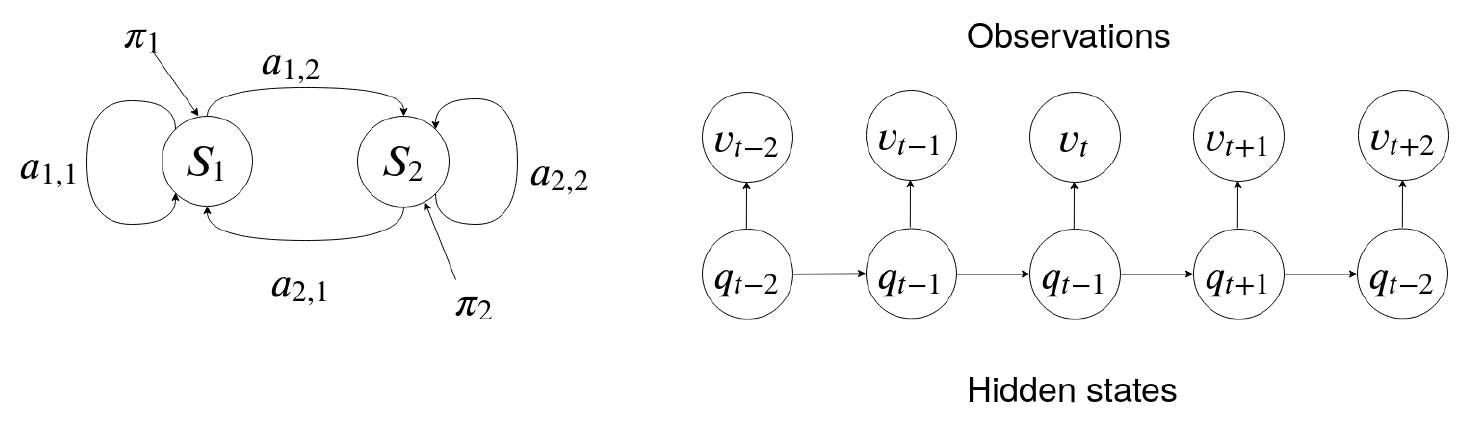
Modelos ocultos de Markov
Dentro de cada estado podemos tener un proceso aleatorio que genera el dato que se va a emitir. El proceso aleatorio es una hipótesis, por ejemplo, suponemos que el proceso aleatoria sigue una distribución de Gauss.
Fíjate en que si no existe proceso aleatorio, es decir, si en cada estado se emite siempre el mismo valor, lo que tenemos es una cadena de Markov.
Modelos ocultos de Markov
En este caso el entrenamiento consiste en encontrar la matriz de transiciones, y los parámetros que definen el proceso aleatorio de cada estado a partir de una secuencia de observaciones.
Antes de la irrupción de las redes neuronales, los mejores modelos de reconocimiento del lenguaje natural estaban basados en modelos ocultos de Markov.
Resumen
Resumen
- La ventaja de las redes recurrentes es que pueden trabajar con vectores de entrada de cualquier tamaño.
- Las redes recurrentes tienen múltiples aplicaciones, desde predecir el siguiente valor en una secuencia, hasta generar imágenes a partir de una descripción.
- La novedad de las redes recurrentes es que añaden estado a cada una de las neuronas. El estado se calcula en función de la entrada actual y el anterior estado.
Resumen
- Sin embargo, para secuencias largas la contribución de los primeros valores de la secuencia se desvanece.
- Las redes LSTM tratan de evitar este desvanecimiento añadiendo una memoria a largo plazo, que se calcula en cada estado y se propaga a las siguientes estados.
Referencias

Aprendizaje Automático (IR2130) - Óscar Belmonte Fernández