Introducción a las Redes Neuronales
Introducción
Las redes neuronales son modelos de aprendizaje automático muy potentes, pero complicados de entrenar.
Su entrenamiento se basa en el algoritmo de retro propagación, que es un una combinación del algoritmo de descenso de gradiente y de la regla de la cadena.
Las redes neuronales pueden resolver tanto problemas supervisados como no supervisados. Además se pueden utilizar tanto en tareas de clasificación como de regresión.
Introducción
El premio Nobel de Física de 2024 se otorgó a John Hopfield y Geoffrey Hinton por sus contribuciones dentro del campo de la redes neuronales.
El premio Nobel de Química de 2024 se otorgó a John Jumper, Demis Hassabis y David Baker por la aplicación del aprendizaje profundo a resolver el problema del plegamiento de proteínas.
Objetivos de aprendizaje
- Esquematizar la estructura de una neurona y un red neuronal.
- Resumir los pasos para crear y entrenar una red neuronal.
- Construir una red neuronal sencilla para problemas de regresión.
- Construir una red neuronal sencilla para problemas de clasificación.
- Interpretar la historia del proceso de entrenamiento.
Referencias
- Deep Learning, Ian Goodfellow, Joshua Bengio and Aaron Courbille.
- Dive into deep learning, Aston Zhang et al.
- Pattern recognition and machine learning. Christopher M. Bishop.
- Hands-on machine learning… Aurélien Géron.
Bases biológicas de las NN
Bases biológicas de las NN
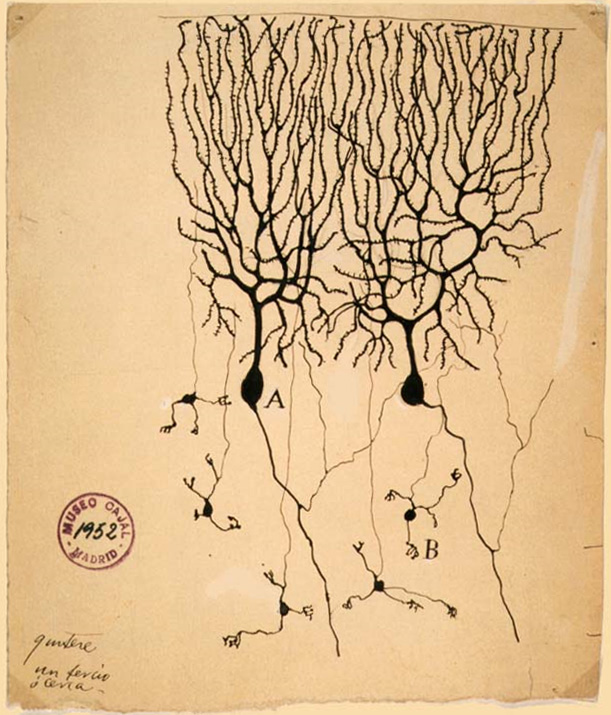
Neuronas vistas al microscopio y dibujadas por Santiago Ramón y Cajal.
Bases biológicas de las NN
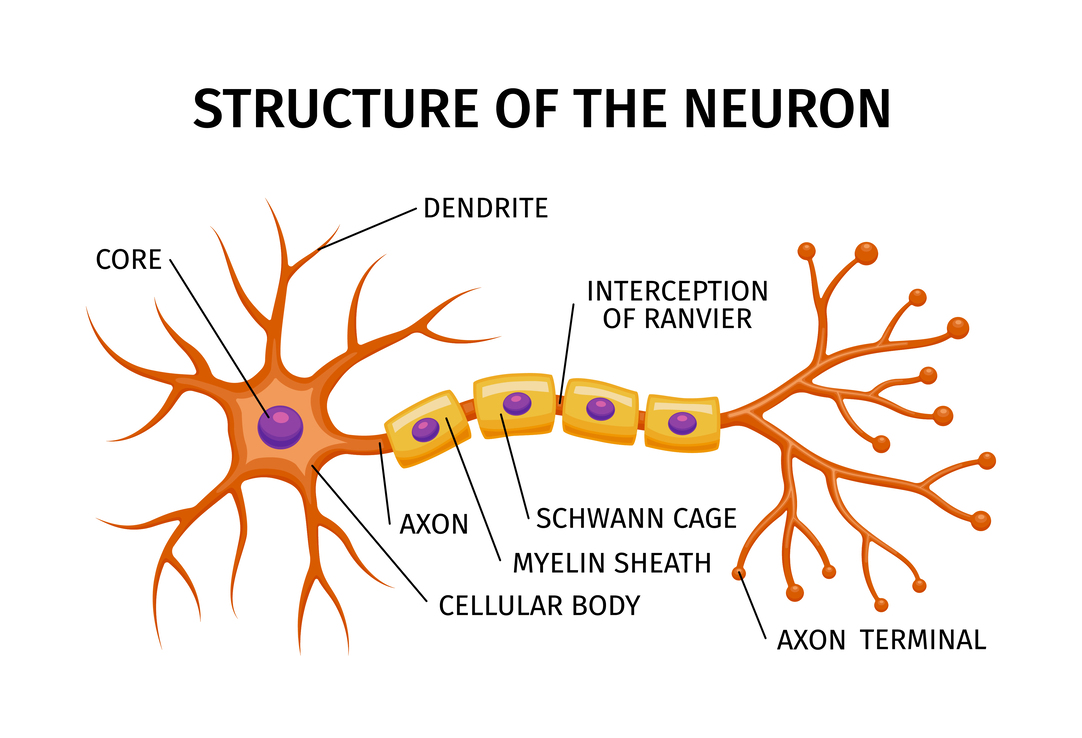
Una neurona recibe señal de otras neuronas a través de la dendrita, y envía señal a otras neuronas a través del axón.
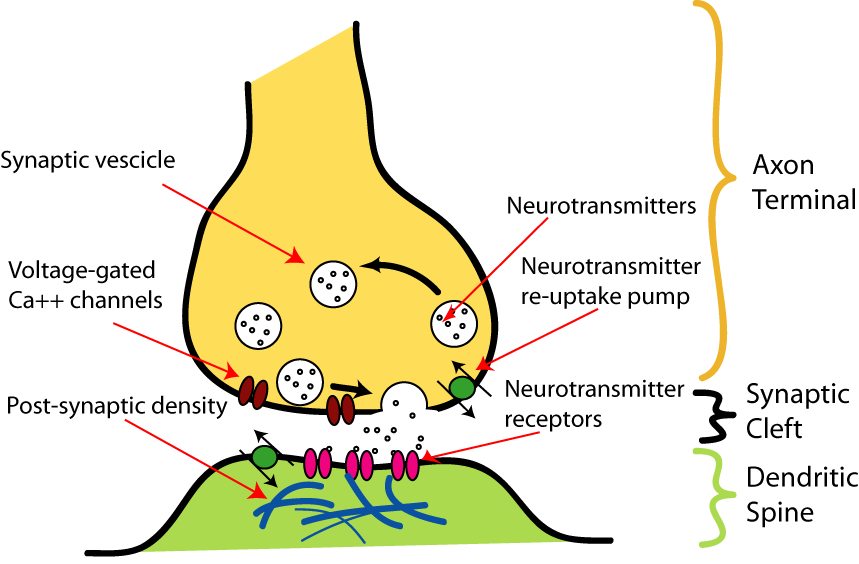
Bases biológicas de las NN
Estructura de las NN
Estructura de una neurona artificial
Una neurona artificial.
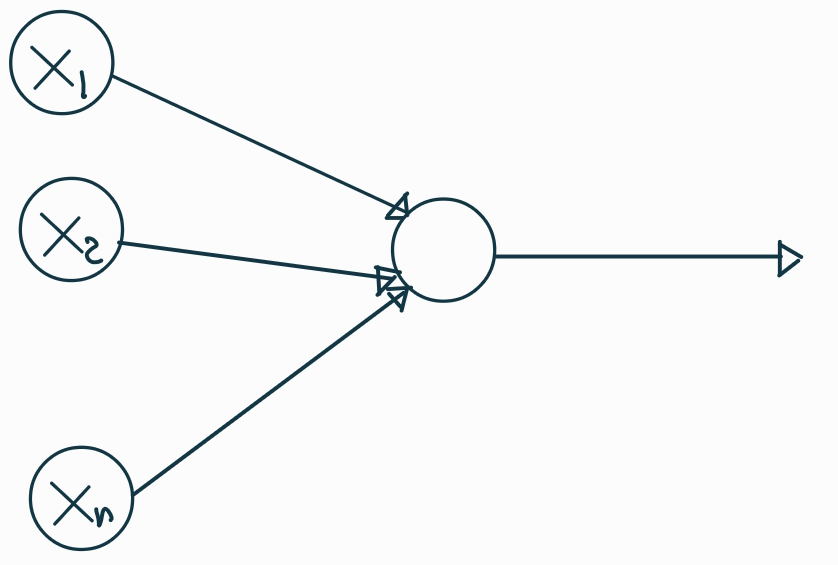
Estructura de una neurona artificial
Activación de la neurona artificial. Cada seña de entrada se multiplica por un peso y se añade un bias.
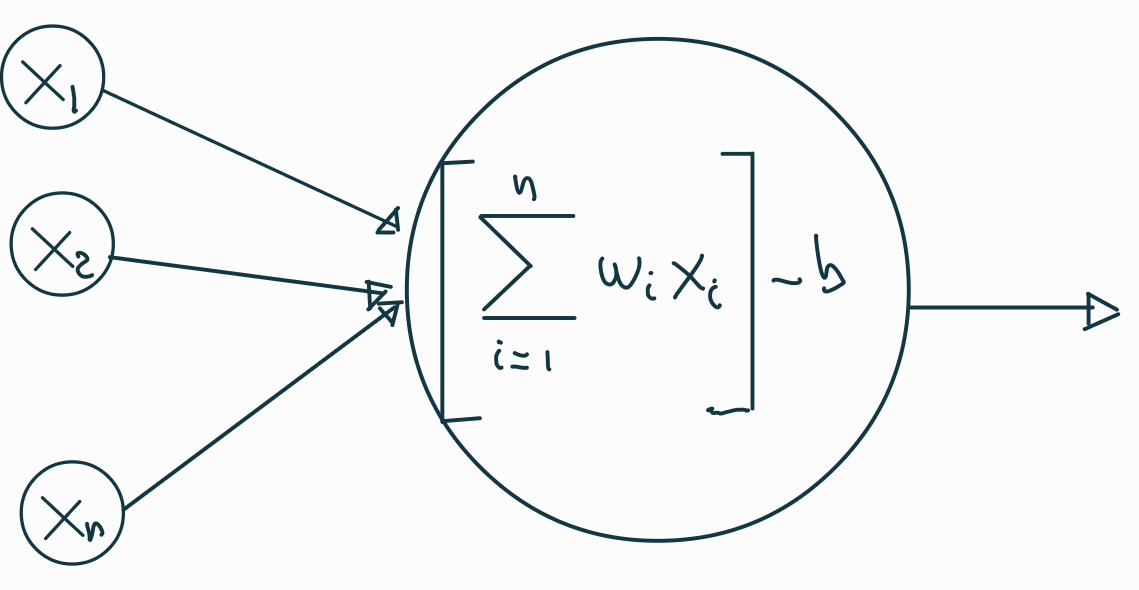
Estructura de una neurona artificial
Aunque apilemos varias capas el resultado es siempre lineal con respecto de los valores de entrada (Demostración).
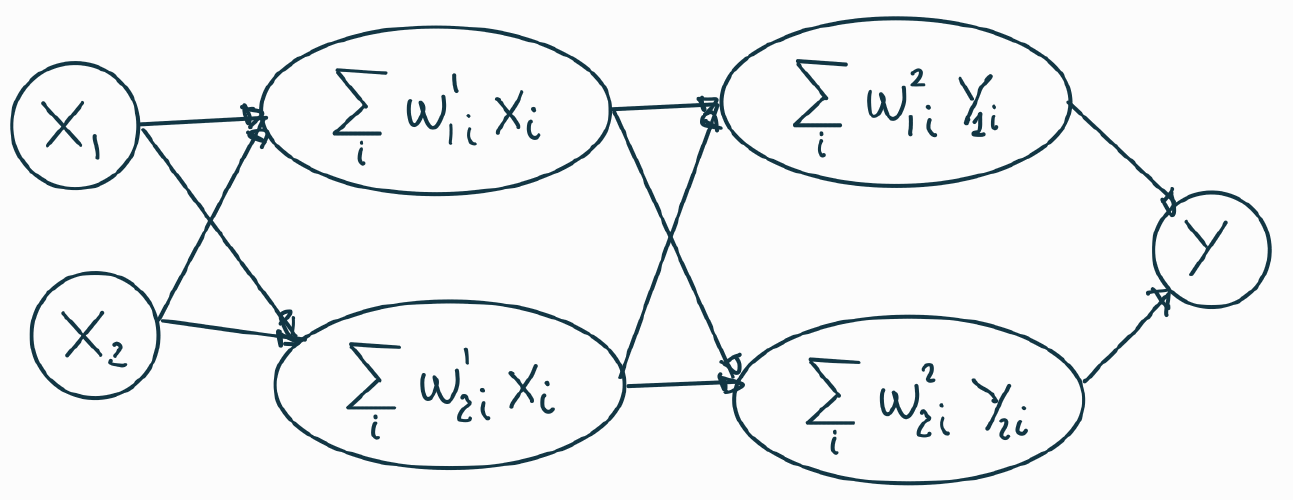
Es necesario introducir la no linearidad de otro modo.
Estructura de una neurona artificial
La función de activación es el ingrediente que introduce la no-linearidad en las redes neuronales.
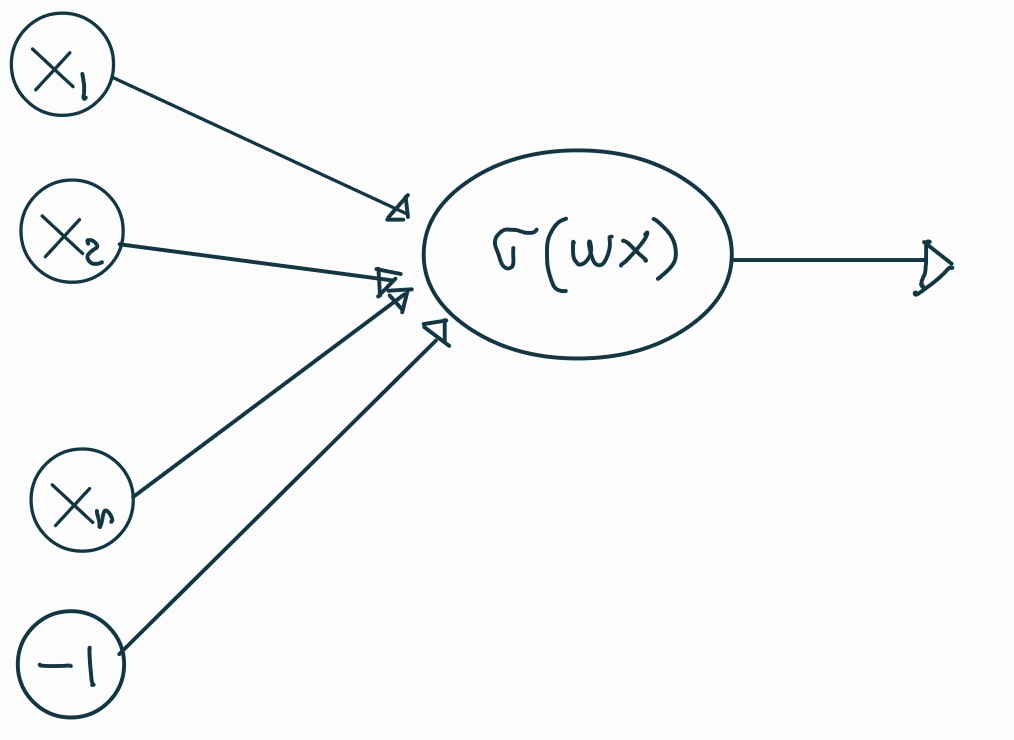
Función de activación sigmoide. \[ \sigma(\omega x) = \frac{1}{1+e^{-\omega x}} \]
Estructura de una NN
El perceptron (Rosenblatt, 1958) fue la primera propuesta de algoritmo inspirado en el funcionamiento de las neuronas biológicas.
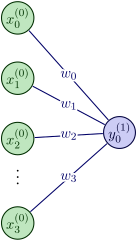
Aunque esta arquitectura es muy sencilla, permite hacer tareas simples de clasificación.
Estructura de una NN
El siguiente paso fue añadir sucesivas capas para mejorar los resultados de las redes. Esta arquitectura se llama Multi Layer Perceptron (MLP).
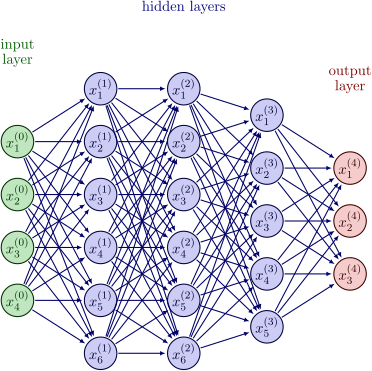
Entrenamiento de una NN
Entrenamiento de una NN
El problema con estas redes es:
- Si se conocen los pesos de la red es muy sencillo calcular la salida.
- Calcular los pesos para que la red ajuste las salidas a partir de las entradas es muy complicado.
La solución al cálculo de los pesos de la red es el algoritmo de retro propagación (back propagation). El algoritmo llamada back propagation fue aplicado en la década de 1980 para entrenar redes neuronales, en particular MLP.
Entrenamiento de una NN
El algoritmo back propagation es una combinación de varios ingredientes, entre ellos:
- Descenso de gradiente.
- Regla de la cadena en derivadas parciales.
Entrenamiento de una NN
De un modo muy somero el algoritmo funciona del siguiente modo:
- Se inicializan, de manera aleatoria, los pesos de la red.
- Para cada dato del conjunto de entrenamiento, se calcula su salida.
- Se calcula el error entre la salida calculada y la real.
- Se utiliza descenso de gradiente para calcular los nuevos pesos de la última capa.
Entrenamiento de una NN
- Se propaga hacia atrás la actualización de los pesos utilizando la regla de la cadena hasta que se actualizan los pesos de todas las capas.
- Se repite el proceso desde el punto 2, hasta un número determinado de pasos o hasta que la actualización de los pesos no es significativa en dos pasos consecutivos.
Entrenamiento de una NN
Detalles a tener en cuenta.
- El problema de optimización no es cuadrático (mínimo de la función de pérdidas), luego no está garantizado que el algoritmo se detenga en el mínimo global.
- El resultado depende de los valores aleatorios iniciales que se asignan a los pesos.
- El algoritmo puede fallar porque al propagar el gradiente este se desvanezca o explote.
Entrenamiento de una NN
En resumen, poder aplicar el algoritmo back propagation para entrenar redes neuronales no es el final de la historia.
Para realizar el ajuste de los pesos de la red necesitamos, entre otros, los siguientes ingredientes:
- Elegir unos buenos pesos aleatorios iniciales.
- Elegir la función de activación.
- Elegir un optimizador adecuado.
Además de la propia arquitectura de la red y otros hiperparámetros en la etapa de entrenamiento.
Las NN son aproximadores universales
Teorema de aproximadores universales
Una red neuronal con un única capa y un número arbitrario de neuronas puede ajustar cualquier función a la salida.
Esta referencia es una muy buena presentación del teorema de aproximadores universales.
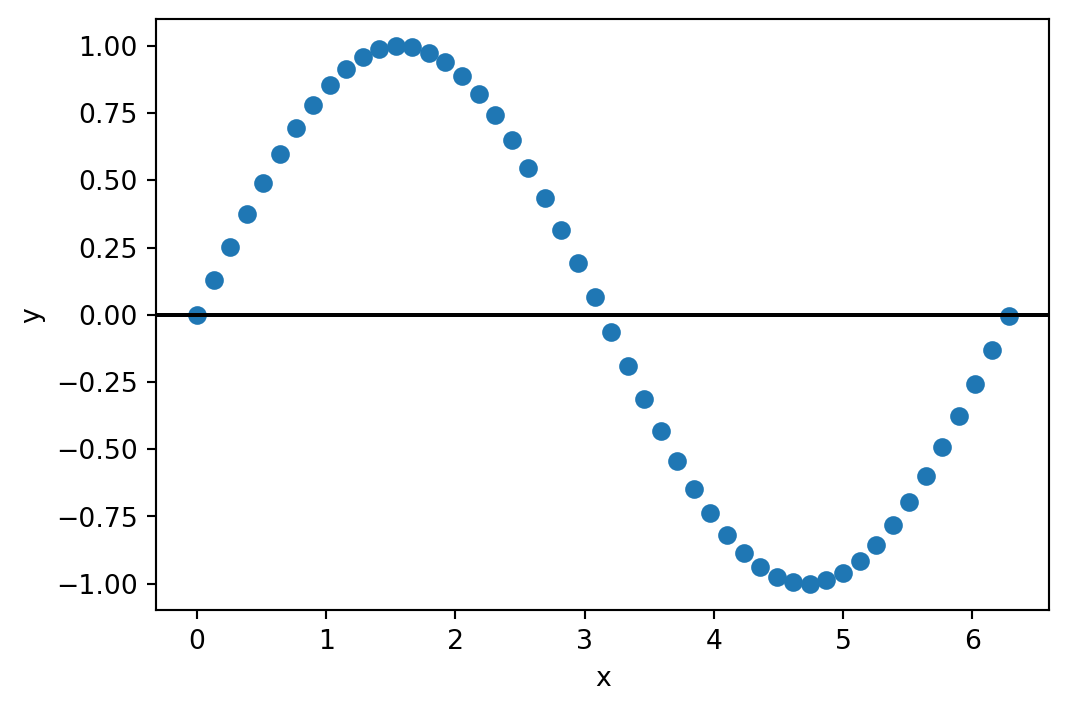
Teorema de aproximadores universales
Este ejemplo muestra 50 puntos de la función \(f(x) = x^2\) y el ajuste realizado por una red neuronal (puntos) con una única capa y 800 neuronas.
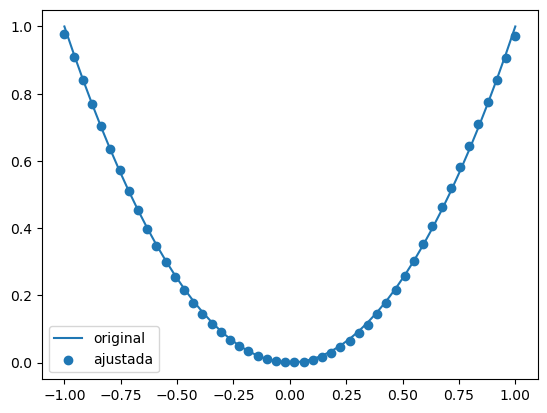
Teorema de aproximadores universales
Este otro ejemplo muestra el caso de la función \(f(x) = seno(x)\). De nuevo los puntos representan 50 valores estimados por la red con una única capa de 500 neuronas.
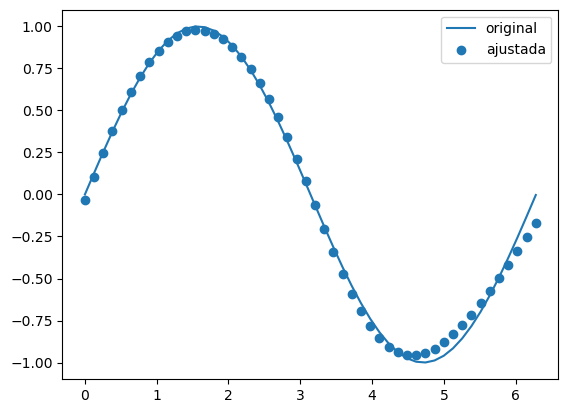
Crear una NN con Keras
Bibliotecas
Keras está incluido dentro de TensorFlow desde la versión 2 de TensorFlow.
Para importar TensorFlow y Keras (una vez que hemos descargado el paquete con micromamba):
Pasos para el entrenamiento de la red
Los pasos para crear y entrenar una red son:
- Definir la arquitectura de la red.
- Compilar la red para seleccionar entre otros:
- Función de pérdidas.
- Optimizador.
- Métrica de evaluación del entrenamiento.
- Entrenar la red con un conjunto de datos.
Creación de la red
Como ejemplo, vamos a crear una red que ajuste los datos de la función seno:
Creación de la red
En Keras hay disponibles dos opciones para crear una red neuronal, la primera de ellas, más sencilla y menos flexible, es utilizar una construcción secuencial:
model = keras.Sequential([
keras.layers.Input((1,)), # Una neurona a la entrada: valor de x.
keras.layers.Dense(500, activation="tanh"), # Una capa oculta completamente conectada.
keras.layers.Dense(1) # La capa de salida con una única neurona: f(x).
])Puedes obtener una descripción de la red que has construido con:
En este caso, el resumen nos indica que esta red tiene 1.501 parámetros que entrenar.
Creación de la red
El siguiente paso es compilar el modelo. En este paso podemos definir las funciones de activación, los optimizadores para el descenso de gradiente, y otros detalles:
optimizer = keras.optimizers.Adam(learning_rate = 0.05)
model.compile(loss="mean_squared_error",
optimizer=optimizer,
metrics=["mse"]
)En un tema siguiente veremos cómo funciona el optimizador Adam.
Entrenamiento de NN
Finalmente, entrenamos la red.
Nota
No se muestra en el código, pero los datos (X, y) se han desordenado para no influir en el proceso de entrenamiento. Además, se toma un 20% de las muestra para validación.
Con el modelo ya entrenado podemos hacer predicciones, y analizar la diferencia con los valores reales.
RMSE: 0.046
Entrenamiento de NN
Este es el resultado del ajuste:

Como puedes ver, el resultado es bastante bueno.
Entrenamiento de NN
Vamos a probar a modelar una red un poco más profunda, con dos capas y sólo tres neuronas en cada capa:
model = keras.Sequential([
keras.layers.Input((1,)), # Una neurona a la entrada: valor de x.
keras.layers.Dense(3, activation=activacion), # Dos capas ocultas completamente conectadas.
keras.layers.Dense(3, activation=activacion),
keras.layers.Dense(1) # La capa de salida con una única neurona: f(x).
])En este caso, el número de parámetros que tenemos que entrenar es 22.
El error ha disminuido, RMSE: 0.026
Entrenamiento de NN
Este es el resultado:
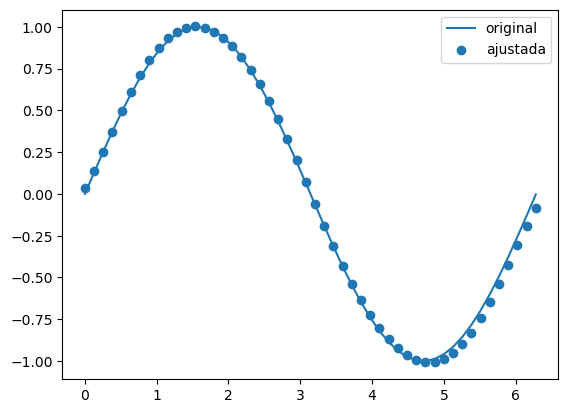
Un poco mejor que con una única capa.
Entrenamiento de NN
Red con una capa y 500 neuronas: 
Red con dos capas de 3 neuronas: 
Los hiperparámetros de entrenamiento son los mismos, pero el número de parámetros que hay que entrenar con la segunda red es mucho menor.
Entrenamiento de NN
El objeto history almacena los datos del proceso de entrenamiento de la NN. En el se ha almacenado el valor de las métricas que hemos seleccionado para cada época del entrenamiento:
Entrenamiento de NN
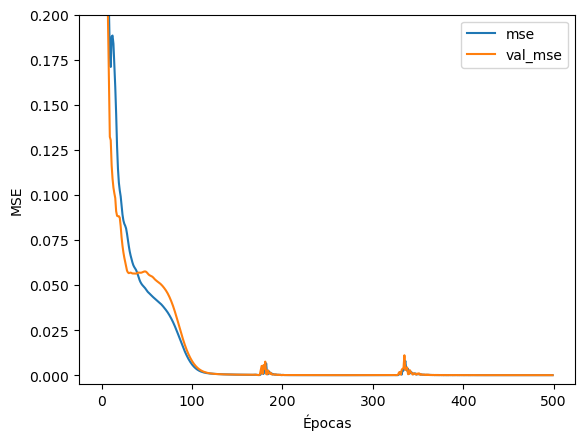
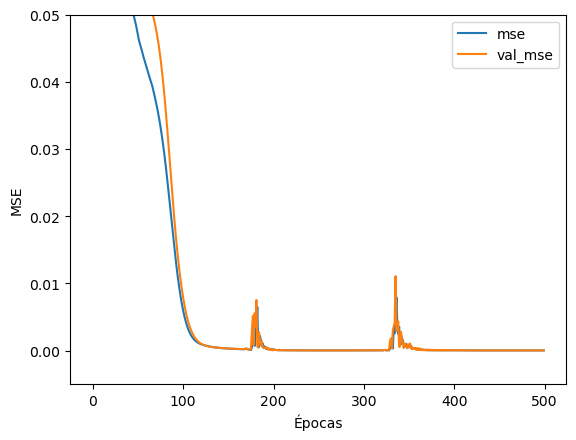
El conjunto de datos de validación nos indica si en el proceso de entrenamiento está ocurriendo sobreajuste. Si las dos curvas están cercanas, no hay sobreajuste. Si la curva de entrenamiento da menores errores que la de validación, puede que haya sobreajuste.
Ejemplo con los datos de Howell
Vamos a probar con los datos de la base de datos de Howell. Empezamos, como en el ejemplo de regresión polinomial, intentado ajustar el valor de peso a partir de la altura.
Primero leemos los datos:
Ejemplo con los datos de Howell
Ahora construimos la red:
tf.keras.utils.set_random_seed(69)
activacion = "tanh"
modelo = keras.Sequential([
keras.layers.Input((X.shape[1],)), # Una neurona a la entrada: valor de x.
keras.layers.Dense(3, activation=activacion), # Dos capas ocultas completamente conectadas.
keras.layers.Dense(3, activation=activacion),
keras.layers.Dense(1) # La capa de salida con una única neurona: f(x).
])Ejemplo con los datos de Howell
Construimos el optimizador, compilamos el modelo y entrenamos:
optimizer = keras.optimizers.Adam(learning_rate = 0.01)
modelo.compile(loss="mean_squared_error",
optimizer = optimizer,
metrics=["mse"]
)
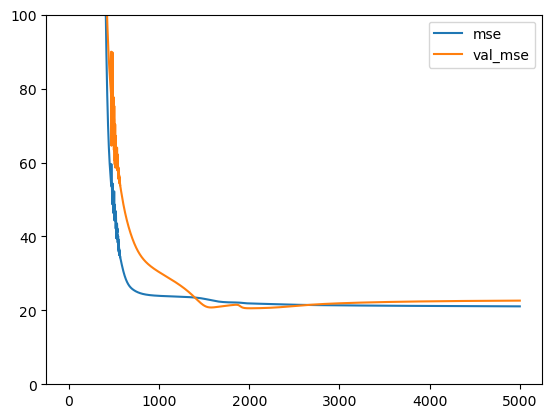
history = modelo.fit(X, y, epochs=5000, validation_split=0.2, verbose=2)Obtenemos un RMSE: 4.93.
Ejemplo con los datos de Howell
Este es el resultado, y la historia del entrenamiento:
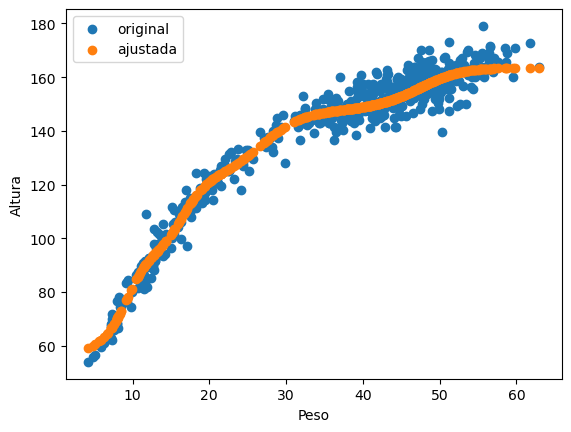
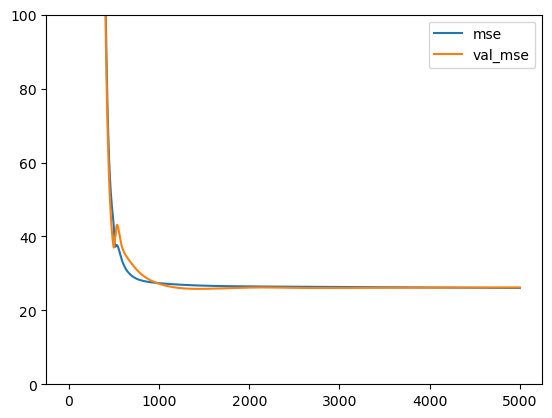
Parecido al resultado que obtuvimos con el regresor polinomial. No se observa sobreajuste.
Ejemplo con los datos de Howell
Ahora vamos a incluir el dato de edad en el entrenamiento:
Y entrenamos de nuevo la misma red.
Tenemos esta vez un RMSE: 4.88. Ha mejorado ligeramente al introducir la edad de cada una de las muestras.
Ejemplo con los datos de Howell
Este es el resultado que obtenemos:
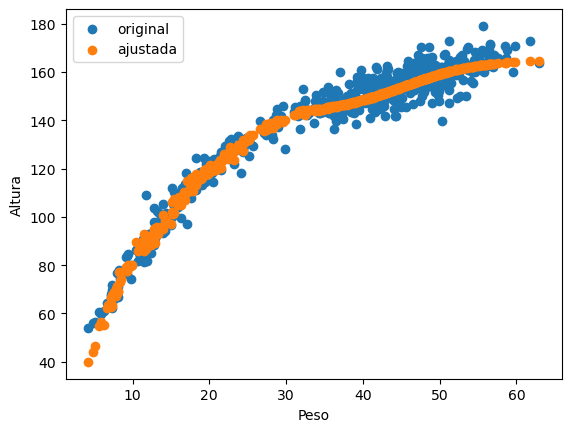
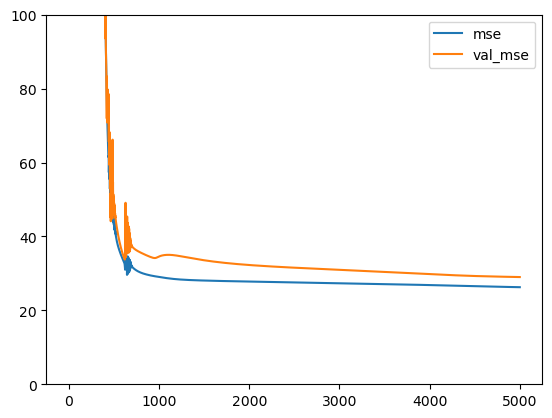
En este caso parece que hay sobreajuste. Algunas veces la solución es volver a entrenar con nuevos pesos aleatorios.
Ejemplo con los datos de Howell
Finalmente, vamos a incluir como predictoras todas las variables excepto la altura, que es la variable predicha. RMSE: 4.342:
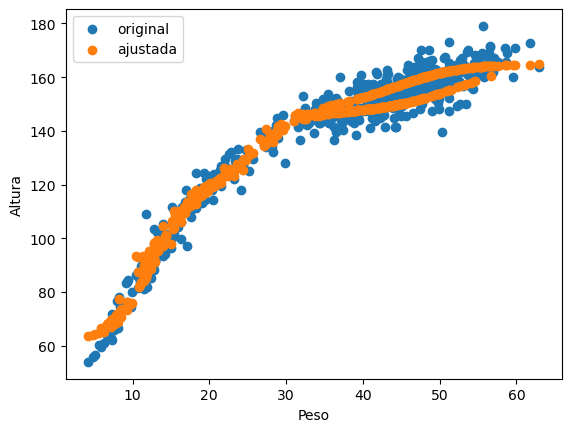
Ejemplo con los datos de Howell
El último resultado es muy interesante. Si visualizamos el resultado teniendo en cuenta el sexo:


Ejemplo con los datos de Howell
Fantástico, la red neuronal utiliza la característica de sexo para ajustar los datos.
Ten en cuenta que estamos utilizando una red con sólo dos capas y tres neuronas en cada capa, 22 parámetros en total.
La red que hemos entrenado se comporta muy bien.
Por comparar, con un ajuste polinómico de grado 8 MSE: 22.863 (9 parámetros), con una red neuronal de 2 capas y 3 neuronas (22 parámetros) por capa MSE: 4.342.
Redes neuronales como clasificadores
Clasificación con NN
Ahora vamos a utilizar una red neuronal, pero esta vez para tareas de clasificación.
Vamos a utilizar el conjunto de datos de Howell, e intentar predecir el sexo de una de las muestras a partir del resto de sus características. Vamos a utilizar sólo los datos de las personas adultas del conjunto de datos.
Clasificación con NN
Construimos la red:
clasificador_howell = keras.Sequential([
keras.layers.Input((3,)), # Tres neuronas de entrada: peso, altura, edad.
keras.layers.Dense(3, activation="relu"), # Dos capas ocultas completamente conectadas.
keras.layers.Dense(3, activation="relu"),
keras.layers.Dense(2, activation="softmax") # La capa de salida con dos neuronas: hombre o mujer.
])Detalles importante:
- Ahora la función de activación en las dos capas ocultas es relu (rectifier linear unit) \(relu(x) = \frac{x + \left|{x}\right|}{2}\).
- La función de activación en la capa de salida es softmax (exponencial normalizada) \(\sigma(x)_i = \frac{e^{x_i}}{\sum_{j}e^{x_j}}\).
Clasificación con NN
Compilamos la red y la entrenamos:
Clasificación con NN
La matriz de confusión que obtenemos es:
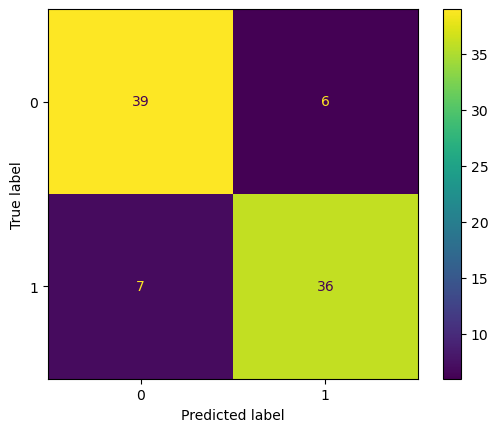
Que es la misma que obteníamos con la regresión logísitca y las máquinas de soporte vectorial.
Resumen
Resumen
- Las redes neuronales (profundas) están inspiradas en el funcionamiento de las neuronas (conexiones, funciones de activación, etc.).
- Las redes neuronales están formadas por capas de neuronas interconectadas entre ellas.
- El entrenamiento de una red implica calcular los pesos entre las conexiones de las neuronas.
Resumen
- Las redes neuronales son aproximadores universales.
- Las redes neuronales se pueden utilizar tanto para problemas de regresión como de clasificación.
- Las redes neuronales son susceptibles al sobreajuste de los pesos.
- Las redes neuronales se entrenan con la técnica de retro propagación, que se puede resumir en regla de la cadena más descenso de gradiente.
Referencias
Algunas referencias interesantes
Herramienta para visualizar redes neuronales.
Las redes neuronales son aproximadores universales.

Aprendizaje Automático (IR2130) - Óscar Belmonte Fernández