Qué es el Aprendizaje Automático (AA).
Dónde se sitúa la disciplina del Aprendizaje Automático
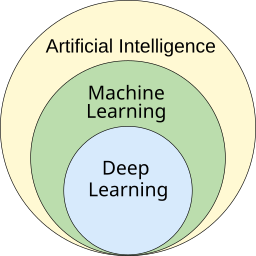
El AA es un subcampo de la IA.
A su vez, el Aprendizaje Profundo es un subcampo del AA.
Definición de Aprendizaje Automático
Decimos que un algoritmo aprende a partir de la experiencia E con respecto a un tipo de tarea T y una medida de rendimiento P, si su rendimiento al realizar la tarea T, medido usando P, mejora con la experiencia E.
![]()
Definición de Aprendizaje Automático
En la definición anterior podemos identificar la experiencia como el conjunto de datos a partir del cuál se quiere el rendimiento al realizar la tarea.
A este conjunto de datos los llamaremos conjunto de datos de entrenamiento.
Qué tipo de problemas podemos abordar con el AA
- Problemas de los que conocemos una solución, pero la solución es difícil de resolver.
- Ejemplo: Clasificar un correo como spam o ham.
- Ejemplo: Encontrar el camino más corto entre dos ciudades en un mapa de carreteras.
- Problemas de los que no conocemos una solución.
- Ejemplo: Detectar anomalías en una serie de datos.
Tipos de AA
- Aprendizaje supervisado.
- Aprendizaje no supervisado.
- Aprendizaje semi-supervisado.
- Aprendizaje por refuerzo.
Aprendizaje supervisado
El conjunto de datos de entrenamiento que se proporciona al algoritmo contiene el resultado esperado para cada una de las muestras.
Por ejemplo, si queremos entrenar un algoritmo para que reconozca dígitos, mi conjunto de entrenamiento debe tener imágenes de dígitos, y cada imagen una etiqueta correspondiente al dígito que representa.
Aprendizaje supervisado
Las tareas más comunes dentro de este tipo aprendizaje son:
- Regresión: A partir de las características de la muestra quiero obtener un valor numérico (o varios).
- Clasificación: A partir de las características de la muestra quiero obtener un tipo/clase/conjunto al que asigno lo muestra.
Aprendizaje no supervisado
El conjunto de datos de entrenamiento que se proporciona al algoritmo NO contiene el resultado esperado para cada una de las muestras.
Por ejemplo, tenemos una base de datos de clientes y queremos agruparlos basándonos en el gasto medio que hacen por compra y el número de compras que hacen al año. Agrupar usando únicamente estas características nos puede mostrar que entre nuestros clientes hay un grupo de personas que realiza compras compulsiva (muchas compras anuales de pequeño coste), y personas «metódicas» que hacen pocas compras anuales pero de gran coste.
Aprendizaje no supervisado
Las tareas más comunes dentro de este tipo de aprendizaje son:
- Agrupamiento: Crear grupos de muestras por «similitud» entre sus características.
- Reducción de dimensionalidad: Cada muestra de mi conjunto tienen muchas características (dimensiones), algunas de ellas pueden ser superfluas, ¿cómo reduzco en número de características sin que las muestras pierdan su identidad?
Aprendizaje semi-supervisado
En nuestro conjunto de datos de entrenamiento tenemos algunas muestras etiquetadas, pero otra muchas no tiene etiqueta.
Por ejemplo, detectar transacciones bancarias fraudulentas. Usualmente, en número de transacciones etiquetadas suele ser pequeño. Un procedimiento para asignar etiquetas a las transacciones no etiquetadas puede realizar un agrupamiento de todo el conjunto de datos, y después asignar etiquetas a las transacciones que no tienen etiqueta según la etiqueta mayoritaria del conjunto en el que han sido clasificadas.
Aprendizaje por refuerzo
La resolución de un problema se realiza mediante ensayo y error.
Cada ensayo tiene una recompensa, que puede ser positiva o negativa. La combinación de ensayo y recompensa condiciona el siguiente ensayo a tomar.
Generalización
La utilidad de los modelos de AA es que nos permitan trabajar con nuevos datos.
Un modelo de regresión es útil porque nos da valores buenos para nuevos datos con los que no ha sido entrenado.
Un modelo de clasificación es útil porque nos permite clasificar nuevos datos con los que no ha sido entrenado.
A este poder de los modelos de AA lo llamamos generalización.
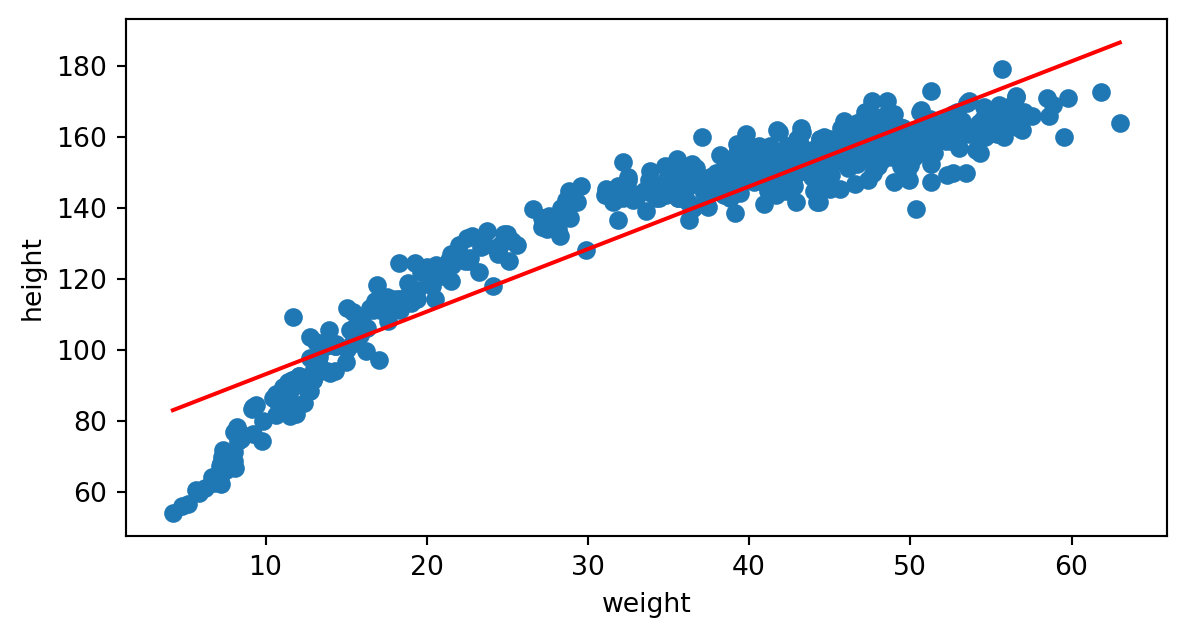
Subajuste (Underfitting)
Un problema que puede aparecer cuando entrenamos un modelo de AA es que no generalice cuando se aplica a nuevos datos porque es demasiado limitado o pobre.
Entonces decimos que el modelo subajusta los datos.
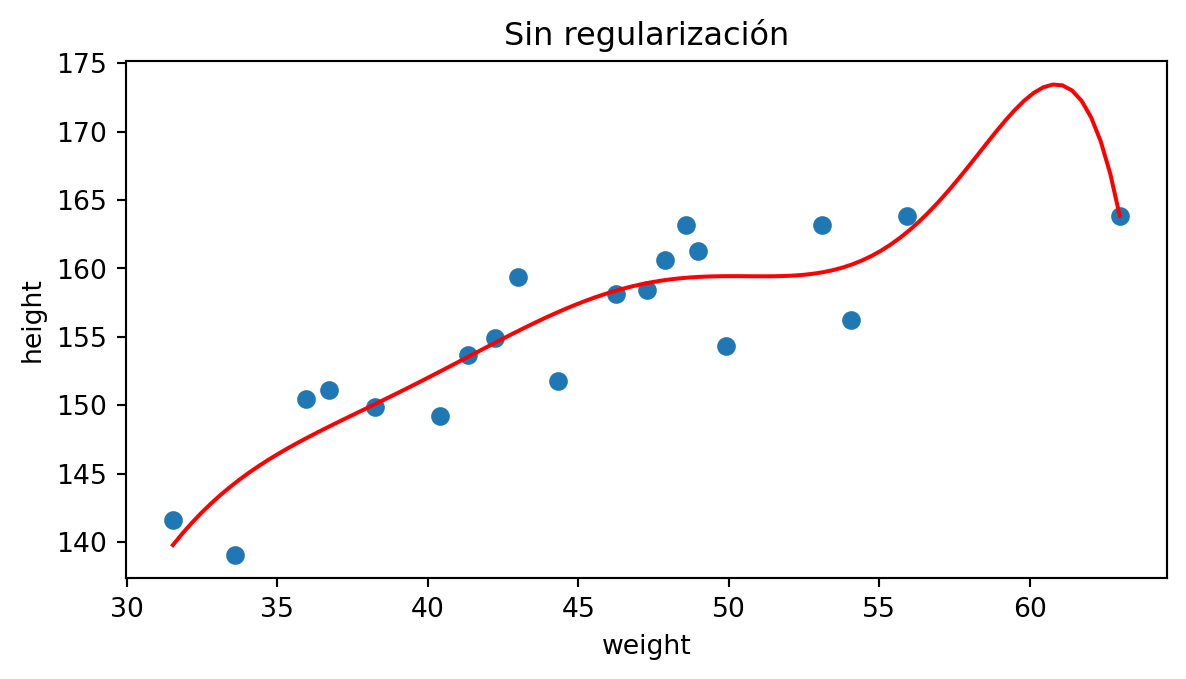
Sobreajuste (Overfitting)
Por el contrario, a veces forzamos el modelo en la fase de entrenamiento para que ajuste muy bien los datos de entrenamiento, lo que a veces implica que el modelo entrenado no funcione tan bien con nuevos datos.
Entonces el modelo sobreajusta los datos.
Métricas
Una vez construido un modelo de aprendizaje automático, debemos medir su desempeño sobre un conjunto de datos de prueba. Este conjunto de datos no ha formado parte del entrenamiento.
Métricas
Si el problema es de regresión, las métricas más utilizadas son:
- Mean Sqaured Error (MSE) o su raíz cuadrada:
\[
MSE = \frac{1}{N}\sum_{n=1}^N (y_n - \hat{y}_n)^2
\]
- Mean Absolute Error (MAE):
\[
MAE = \frac{1}{N} \sum_{n=1}^N |y_n - \hat{y}_n|
\]
Métricas
Si el problema es de clasificación, usualmente se presentan los resultados con forma de matriz de confusión:
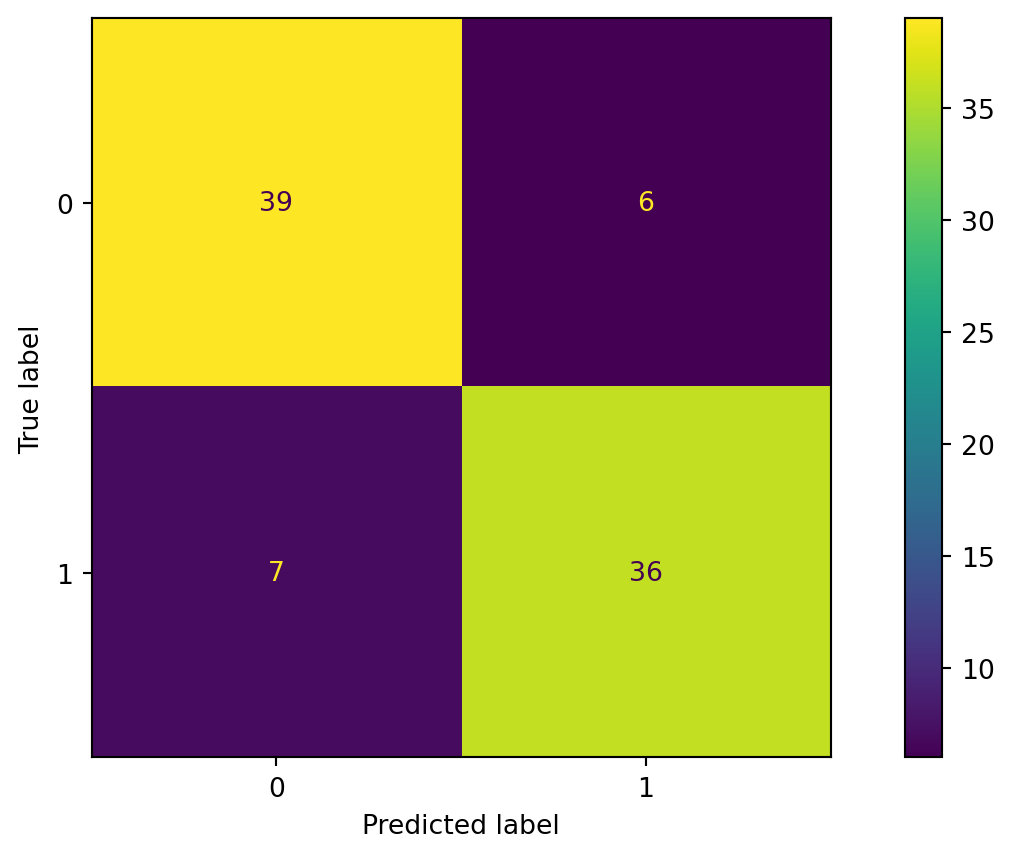
Métricas
\[
Precisión = \frac{TP + TN}{P + N} \\
Sensitividad = \frac{TP}{P} \\
Especifidad = \frac{TN}{N} \\
F1 = 2\frac{sentividad \cdot especifidad}{sensitividad + especifidad}
\]
Métricas
Otra métrica menos utilizada pero bastante informativa en clasificación binaria es el Área Bajo la Curva (AUC - Area Under the Curve).
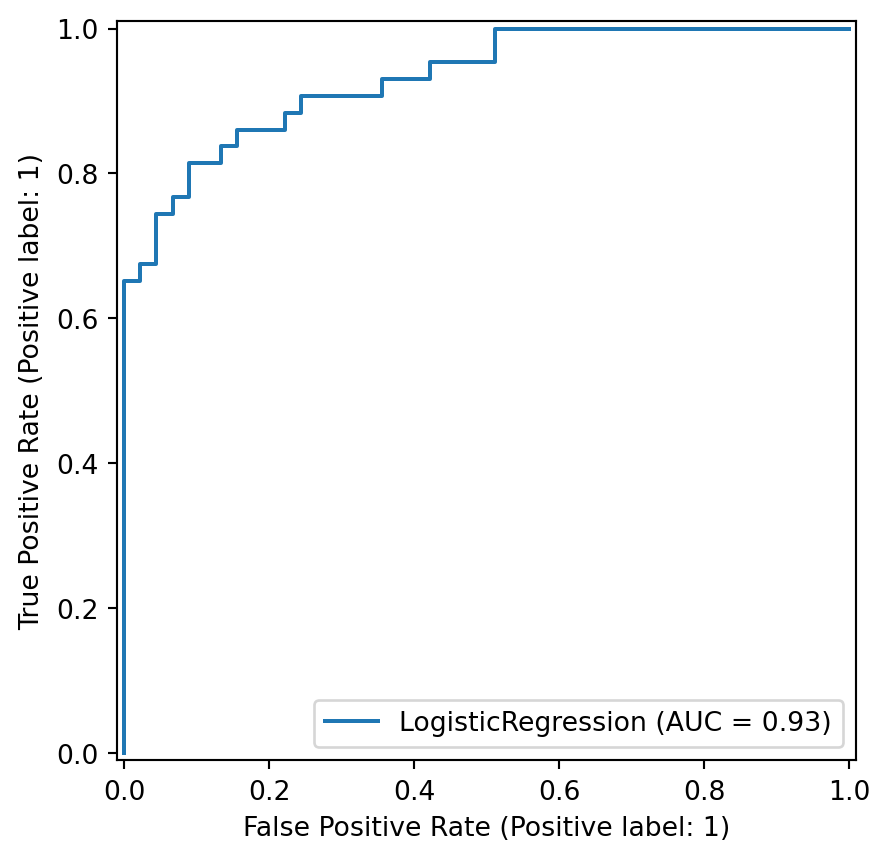
Métricas
La idea básica de la clasificación binaria es establecer de algún modo una ordenación de los datos según algún criterio. El segundo paso es establecer un umbral dentro de la ordenación, de tal modo que las muestras que superen ese umbral se clasifican como positivas, y las que no, se clasifican como negativas.
Resumen
- El Aprendizaje Automático es un subcampo de la Inteligencia Artificial.
- El objetivo de AA es crear modelos que pueden aprender de la experiencia entendida como datos.
- Los principales tipos de problemas dentro del AA son regresión y la clasificación.
- Los principales tipos de aproximaciones son el aprendizaje supervisado, el no-supervisado, semi-supervisado y por refuerzo.
Resumen
- Es conveniente establecer alguna(s) métrica que dé cuenta de la calidad del modelo.
- Es importante que el modelo tenga un buen desempeño no sólo sobre los datos sobres los que se ha entrenada si no también sobre nuevos datos.
