Aprendizaje por refuerzo

Introducción

Durante el curso, hemos visto algoritmos de aprendizaje automático que se basan en un conjunto de datos de entrenamiento para construir un modelo.

En el caso del aprendizaje por refuerzo no existe ningún conjunto de datos con el que construir el modelo, en vez de ello, operamos en un entorno que nos devuelve una recompensa dependiendo de la acción que realicemos y el estado en el que nos encontremos.

Son necesarios nuevos algoritmos para encontrar las soluciones dentro de este nuevo paradigma.

Objetivos de aprendizaje

Interpretar cuales son las características particulares del aprendizaje automático.
Resumir los conceptos de agente, estado, acción y recompensa.
Conectar cada uno de los conceptos anteriores con el proceso de aprendizaje.
Construir una solución utilizando el algoritmo Q-learning.

Objetivos de aprendizaje

Argumentar la utilidad del descuento.
Interpretar el dilema explotación frente a exploración.
Argumentar la utilidad del parámetro \(\epsilon\).

Referencias

Hands-on machine learning, Aurélien Géron.
Reinforcement learning: An introduction.

Introducción

En el aprendizaje supervisado construimos un modelo con datos y valores de salida. Nuestro modelo nos dará un nueva salida para cada nuevo dato.

En aprendizaje no supervisado construimos un modelo sólo con datos, y el modelo aprende a identificar las similitudes entre los datos.

Introducción

En aprendizaje por refuerzo tenemos estados (dentro de un entorno), acciones (ejecutadas por un agente) y recompensas, y el objetivo es maximizar la recompensa global tomando las mejores acciones en cada uno de los estados por los que vamos pasando.

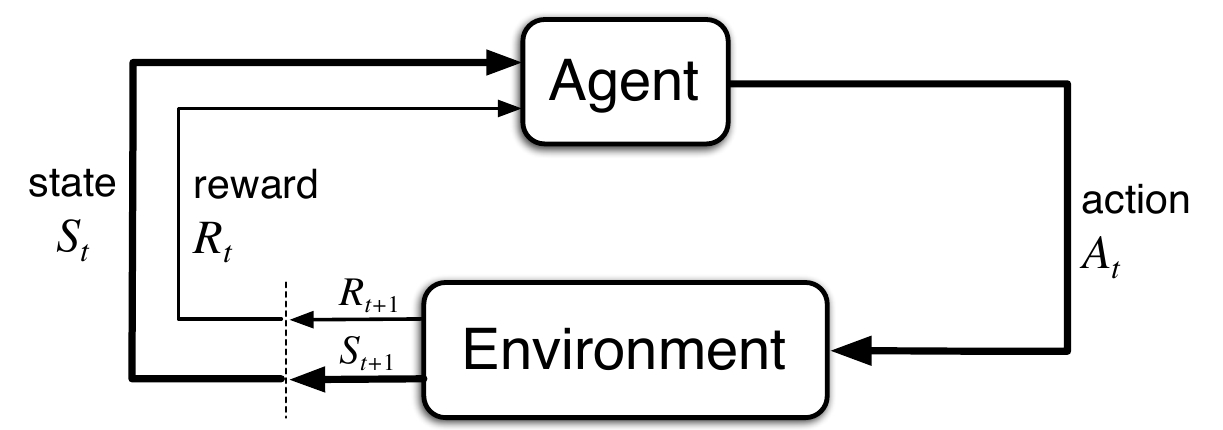
Introducción

Ejemplos del mundo real: juegos, robótica, optimización.

Estrategia en juegos.

AlphaGo

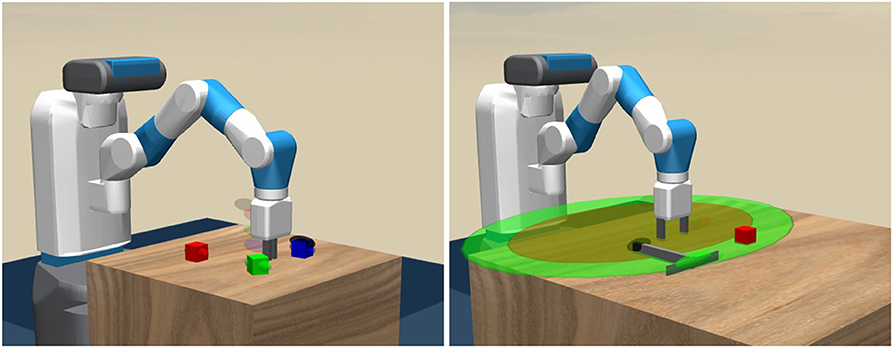
Planificación en robótica.

Introducción

Medicina y salud.

AlphaFold.

Conducción autónoma.

Conceptos clave

Agente, Acción, Estado y Recompensa

El agente es quien decide qué acción tomar.

El agente debe escoger la siguiente acción a llevar a cabo dependiendo del estado actual del entorno con el objetivo de maximizar la recompensa.

\[ A = \{a_1, a_2,...,a_n\} \]

Representa el conjunto de posibles acciones.

Agente, Acción, Estado y Recompensa

La secuencia de pasos durante el proceso de aprendizaje es:

Se observa el estado del entorno.
Se realiza una acción.
Se obtiene una recompensa.

\[ \{S_1, A_1, R_1, S_2, A_2, R_2,...,S_t,A_t,R_t\} \]

Agente, Acción, Estado y Recompensa

Un detalle importante: observa que el entorno puede cambiar, si el agente es un jugador virtual de ajedrez, a cada movimiento del agente le sigue un movimiento del contrario.

Agente, Acción, Estado y Recompensa

Si el conjunto de estados, acciones y recompensas es finito, se conoce el estado actual y la acción elegida, entonces, se puede calcular la probabilidad del siguiente estado y la recompensa obtenida.

\[ p(s',r|s,a) = p(S_t=s', R_t=r | S_{t-1} = s, A_{t-1} = a) \]

Con la condición: \(\sum\limits_{s' \in S} \sum\limits_{r \in R}^{} p(s',r|s,a) = 1\)

A esta elaboración matemática se la llama procesos de decisión de Markov.

Agente, Acción, Estado y Recompensa

Ejemplos de agente pueden ser:

Un coche autónomo.
Un robot en un entorno industrial.
Un dron.
Un jugador virtual de go o ajedrez.
Un personaje en un video juego.

Episodios y Ganancia

En casos como los de un coche autónomo, o un jugador virtual existe uno, o varios, estados finales. Un coche lleva a los pasajeros del punto de recogida al punto de entrega; un jugador virtual gana o pierde una partida, a este concepto lo llamaremos episodio.

En esta caso resulta sencillo definir el concepto de Ganancia a futuro como la suma de las recompensas que obtiene el agente durante el episodio a partir de un cierto instante y hacia adelante:

\[ G_t = R_{t+1} + R_{t+2} + ... + R_T \]

Donde \(T\) es el tiempo final del episodio.

Episodios y Ganancia

Hay otros casos, como el de un robot en un ambiente industrial, donde no podemos identificar episodios, el agente está realizando de modo continuo acciones y la secuencia de acciones nunca acaba.

En este caso, para acotar la ganancia para que no crezca hacia el infinito, se introduce el concepto de factor de descuento, que es una especie de decaimiento exponencial de la recompensa a futuro.

\[ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \]

Una analogía monetaria, 100 euros de hoy no tendrán el mismo valor dentro de 10 años, se habrán devaluado.

Episodios y Ganancia

El factor de descuento \(\gamma\) también se utiliza cuando el espacio de estados es finito.

El dominio suele ser \(0 \leq \gamma \leq 1\), siendo un valor típico \(\gamma = 0.99\).

Política

La acción se escoge según cierta política \(\pi\):

\[ \pi: S \rightarrow A \]

La política \(\pi\) puede ser:

Determinista, \(a = \pi(s)\) la acción a escoger depende del estado actual.
No determinista \(a = p(a|s)\), se escoge la acción según cierta probabilidad asignada a cada una de ellas.

Función acción-valor

Finalmente, lo que buscamos es encontrar una política que maximice la ganancia esperada a futuro:

\[ q_\pi(s,a) = E_\pi(G_t|S_t = s, A_t = a) \]

Esta función se llama función acción-valor para la política \(\pi\).

El objetivo es maximizar la función acción-valor eligiendo la secuencia de acciones adecuada.

El algoritmo Q-learning

Función Q

Una aproximación al óptimo de la función acción-valor es el algoritmo Q-learning:

\[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[ R_{t+1} + \gamma \max_{a \in A} Q(S_{t+1},a) - Q(S_t,A_t) ] \]

Donde \(\alpha\) es la tasa de aprendizaje y \(\gamma\) es el factor de descuento.

La función \(Q(s,a)\) es una medida de lo bueno que es estar en el estado \(s\), y realizar la acción \(a\); mide la calidad (Q-uality) de la pareja estado-acción.

Función Q

\[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[ R_{t+1} + \gamma \max_{a \in A} Q(S_{t+1},a) - Q(S_t,A_t) ] \]

\(\gamma \max_{a \in A} Q(S_{t+1},a) \rightarrow\) mejor estado que se puede conseguir al realizar una acción \(a \in A\) (con descuento).

\(R_{t+1} \rightarrow\) recompensa inmediata al realizar la acción \(a \in A\).

Ejemplo

En el estado mostrado (14), la mejor acción que puede tomar el elfo es moverse hacia la derecha, por lo que la calidad (Q) de la pareja (estado=14, acción=derecha) se incrementa.

Función Q

\[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[ R_{t+1} + \gamma \max_{a \in A} Q(S_{t+1},a) - Q(S_t,A_t) ] \]

Fíjate en que la función \(Q(S_t,A_t)\) se actualiza al elegir la mejor acción \(a\) en cada paso del aprendizaje.

Un detalle muy interesante de esta función es que converge hacia el óptimo con independencia de la política que utilicemos.

Función Q en espacios finitos

Para ver cómo funciona el algoritmo Q-learning vamos a utilizar, inicialmente, un problema con un número de estados finito.

Lago Helado: El agente debe llegar desde la posición de inicio hasta el regalo, si se alcanza el regalo, la recompensa es 1.

Las posibles acciones son moverse a la izquierda, abajo, derecha, o arriba desde la posición actual.

El juego acaba si se cae en un agujero, o si el número de acciones antes de alcanzar el regalo alcanza un límite, la recompensa es 0.

Función Q en espacios finitos

El problema tiene 16 estado posibles (uno por cada casilla), y las acciones que el agente puede tomar son 4.

	Izquierda	Abajo	Derecha	Arriba
1	0	0	0	0
2	0	0	0	0
…	0	0	0	0
15	0	0	0	0
16	0	0	0	0

Inicialmente la matriz está llena de ceros.

Función Q en espacios finitos

Nuestra tabla Q tiene 16 x 4 = 64 elementos.

Si aplicamos el algoritmo:

while not terminado:  
    accion = np.argmax(Q[estado,:])
    nuevo_estado, recompensa, terminado,_,_ = lago.step(accion)
    Q[estado, accion] += alfa * (recompensa + 
        gamma*np.max(Q[nuevo_estado,:]) - Q[estado, accion])
    estado = nuevo_estado

\[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[ R_{t+1} + \gamma \max_{a \in A} Q(S_{t+1},a) - Q(S_t,A_t) ] \]

Veremos que, simplemente, el algoritmo no aprende. ¿Por qué?

Función Q en espacios finitos

El problema en esta expresión:

\[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[ R_{t+1} + \gamma \max_{a \in A} Q(S_{t+1},a) - Q(S_t,A_t) ] \]

Está en esta parte:

\[ Q(S_t,A_t) \leftarrow ... \max_{a \in A} Q(S_{t+1},a) ... \]

Como todas las posiciones de la tabla son 0, nunca se actualiza la tabla, dicho de otro modo, el algoritmo no aprende.

Función Q en espacios finitos

Este problema se conoce con el nombre de Dilema de exploración frente a explotación.

Si siempre queremos explotar (maximizar) el resultado, puede que nunca exploremos nueva soluciones que nos pueden acercar al óptimo.

¿Cómo lo solucionamos?

Función Q en espacios finitos

Introduciendo un factor de exploración en el algoritmo.

def selecciona_accion(estado):
    if rng.random() < epsilon: 
        accion = lago.action_space.sample()
    else:
        accion = np.argmax(Q[estado, :])

    return accion

Y la introducimos en el algoritmo Q:

while not terminado:  
    accion = selecciona_accion(estado)
    nuevo_estado, recompensa, terminado, _, _ = lago.step(accion)
    Q[estado, accion] += alfa * (recompensa + gamma*np.max(Q[nuevo_estado,:]) - 
        Q[estado, accion])
    estado = nuevo_estado

epsilon = max(epsilon - epsilon_decay, 0)

Función Q en espacios finitos

A esta técnica se le llama Q-learning \(\epsilon\) - voraz

El valor inicial de \(\epsilon\) puede ser \(1\) y decaer en cada episodio de aprendizaje con alguna tasa \(\epsilon\)-decay \(=0.00001\).

Al principio la política es de exploración, y cuando la tabla Q ya contiene algunos valores, \(\epsilon\) ha decaído de manera que se pasa a la fase de explotación.

Función Q en espacios finitos

Con esta mejora, el algoritmo ya es capaz de aprender, y encontrar la solución:

Fíjate en que no hay una única solución posible ya que la fase de exploración es estocástica.

Veamos ahora cómo podemos tratar el caso de entornos con espacios de estados continuo.

Función Q en espacios continuos

Hay casos en los que el espacio de estados no es continuo.

Cartpole: Hay que mantener el bastón en la vertical, sin que se caiga.

El espacio de estado está formado por la posición de la base, su velocidad, el ángulo que forma el bastón con la vertical, y la velocidad angular.

Todas las variables de este espacio son continuas.

¿Cómo procedemos?

Función Q en espacios continuos

Discretizamos el espacio, convertimos las variables continuas en discreta sobre un número suficiente de valores posibles (densidad).

espacio_posiciones = np.linspace(-2.4, 2.4, 10)
espacio_velocidades = np.linspace(-4, 4, 10)
espacio_angulos = np.linspace(-.2095, .2095, 10)
espacio_velocidad_angular = np.linspace(-4, 4, 10)

Y, a partir de este momento, procedemos de igual forma que lo hemos hecho en el caso discreto.

Detalle importante, la matriz Q en este caso tiene 10 x 10 x 10 x 10 = 10.000 posiciones.

Función Q en espacios continuos

Cuando el espacio de estados es muy grande, la aproximación con tablas Q no se puede aplicar.

Pero, podemos aplicar redes neuronales para ayudar en la resolución.

Resumen

El aprendizaje por refuerzo no parte de un conjunto de datos de entrenamiento.
Los conceptos clave son el agente, los estados, las acciones y las recompensas.
El objetivo de los algoritmos de aprendizaje automático es maximizar la recompensa a futuro.

Resumen

Un algoritmo que se aproxima al óptimo del máximo de recompensa a futuro es el algoritmo Q-learning.
Q-learning tiene una aplicación directa en el caso de entornos discretos, pero si los queremos aplicar a entornos continuos, debemos discretizar los espacios de estados.