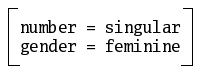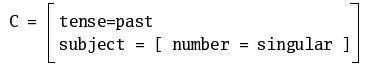GFU-LAB: A Formalism for the Computational Treatment of Syntax and Semantics
J. C. Ruiz Anton
Universitat Jaume I
Castellˇ, Spain
e-mail: ruiz@trad.uji.es
1. Introduction
This document describes GFU-LAB, a software package designed for developing and testing constraint grammars, in a formalism derived from original Lexical-Functional Grammar (LFG) (as described in Kaplan & Bresnan 1982 or Sells 1985, chapter 4; see also Falk 2001, Dalrymple 2001), albeit extended with techniques and devices that have proved to be useful in other unification formalisms.
GFU-LAB consists of a bottom-up parser that checks the grammaticality of particular sentences, according to the rules and lexicon provided in advance. If a given sentence is accepted, its F-structure and semantic representation may be displayed.
A description of a language is made in GFU-LAB by means of a grammar and a lexicon. Basically, the grammar contains a set of phrase-structure rules, annotated with constraints, and the lexicon contains feature specifications for each word. Lexical entries can have a wealth of morphological, syntactical and semantical information.
2. GFU-LAB as a generative model
2.1 Preliminaries
The grammar model which underlies GFU-LAB is generative, in its classical definition:
"A Generative Grammar is a device (or procedure) which assigns structural descriptions to sentences in a perfectly explicit manner, formulated independently of any particular language" (Chomsky 1964, p. 995)
2.2 Functional Descriptions
Unlike the standard version of most generative grammars, GFU-LAB does not represent phrases by constituency trees. Instead, it uses complex feature matrices, called F-structures or Functional Descriptions (FDs) (Kay 1985).
Features are data structures of the form A=V, where A
is an attribute (as 'number') and V is a value (as
'singular' or 'plural'). Thus, (1) shows a typical feature:
(1) number = singular
We can envisage features as minimal information units.
Features group together in matrices, as in:
Feature order is irrelevant. In addition, matrices may have only an attribute of each kind: a matrix containing two identical attributes is ill-formed.
A fundamental property of feature matrices is its capability for hierarchical organization. That means that the value of an attribute may be a FD, rather than an atomic symbol as 'plural' or 'feminine'. To put it differently: it is possible to have an FD embedded in another. These FD-valued features will are termed complex features.
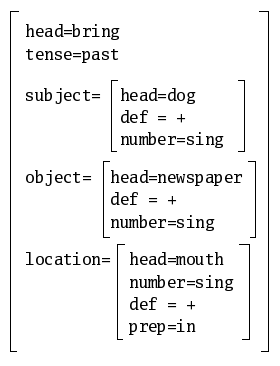
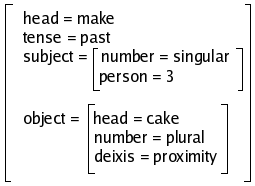
For instance, an analysis of the sentence the dog brought the newspaper in the mouth might be the FD:
Where subject, object and location
are functional labels, which introduce complex features.
This hierarchization potential makes feature structures suitable as a means of full linguistic representation.
2.3 Unification
Unification is a formal operation that combines the features in two FDs in order to get a FD that comprise all features in both matrices.
For example, consider the following structures:
The unification of A and B results in the FD
It must be noted that unification proceeds in a recursive manner: by
unifying complex features (as subject in our example),
the FD in their values are unified as well.
When two FDs include the same attribute, but with incompatible
values, unification fails. Thus, the matrix C cannot
unify neither with A nor with B. In the
first case, there is a conflict with the feature number
in the subject, and in the second case, the conflict arises with the
attribute tense.
A full functional description of a phrase arises from the interaction of feature constraints, mostly derived from the lexical entries and also from the syntax rules which combine them. The final FD is the result of incrementally unifying all this information.
All the unification formalisms adopt the working hypothesis that it is feasible to process the syntactic and semantic information together, thus making two distinct representation levels and some procedure to transform one level onto the other unnecessary. Consequently, semantic information can be fully integrated in lexical entries and syntax rules.
3. Phrase Structure Rules
The bulk of the syntactic description of a language is made in GFU-LAB by Phrase Structure rules (PS rules), as usual in Generative Grammars. They are just rules which define the conditions of combination of constituents in a particular language.
PS rules are suitable for grammatical descriptions for several reasons: They are quite familiar to linguists; their mathematical and formal properties are well known; they are relatively easy to write and maintain, and there are many efficient algorithms for compiling and parsing them.
In GFU-LAB, Phrase Structure rules have the form:
A --> B.
Where A refers to the phrase category, and B
is a sequence of one or more constituent of this phrase. Rules are only
marked with a dot at the end.
For instance, the following rule states that a sentence (S)
consists of a Noun Phrase (NP) and a Verb Phrase (VP):
S --> NP VP.
In this elementary example, each constituent refers to only one phrasal category. However, GFU-LAB allows to include much more information about the constituents. Thus, it is possible
| (a) |
to identify optional constituents, with the sign ' NP --> &DET N. That rule specifies that a Noun Phrase ( |
||||||
| (b) | to mark multiple constituents, with an asterisk:
VG --> &NEG *CLIT V. This rule says that a Verb Group ( It is important to bear in mind that the set defined by a star may be empty (i.e. it counts for zero occurrences of a constituent). |
||||||
| (c) | to have constituent disjunctions. A disjunction has the form
Where Xi is a disjunct constituent. The sign ' A --> (B | C) D. This describes the phrase Disjunctions may be also characterized as optional:
This rule allows that a phrase The constituents in a disjunction may be optional or multiple as well:
Note that rule (3a) is equivalent to (2). |
4. Constraints
The nodes in a PS rule may include constraints which narrow the application of the rule and control (by unification) how the FD of the whole phrase is built up.
Let us introduce, before going into details, a bit of terminology. Consider a PS rule as
A --> B C.
Constraints are attached to the constituent category symbols. Here, B
and C may be paired with sets of constraints.
We call mother the phrase described by the rule, whose
category symbol is on the left of arrow (here the mother is A).
We call associate of C that constituent that a
set of constraints C is attached onto.
When stating constraints, two metavariables U and D
are employed. The metavariable U refers to the mother. Its use is similar to
↑ in standard LFG.
The metavariable D refers to the associate of each
constraint, just like the lower arrow (↓) in LFG. Consider, for an example, the rule:
(4) S --> NP : U/subject=D
VP.
The colon separates the constituent category symbol from the set of
constraints. The constraint U/subject=D means that the
feature subject in the mother (S) unifies
with the FD of the associate (NP).
When a constituent has no constraint attached, its FD will unify
with the mother FD. So, for (4), the FD of the VP will
unify with the FD of the S.
Let us see how the constraints work, with a small example. Consider a grammar constituted by the rule (4), in addition of:
(5)
a. VP --> V
NP : U/object=D.
b. NP --> DET N.
Rule (5a) states that a VP consists of a verb (V)
and a object noun phrase. On the other hand, (5b) says that noun
phrases are formed by a determiner (DET) and a noun (N).
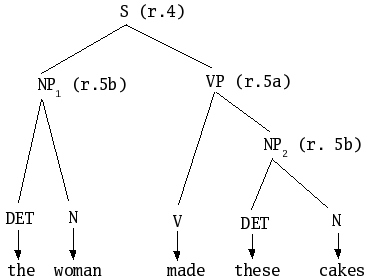
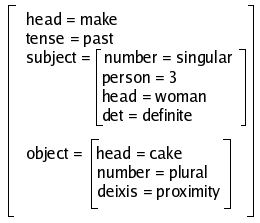
These rules give the following parse tree to the sentence the woman made these cakes:
Furthermore, will assume that the lexical entries for the terminals are:


Notice that the number-person agreement information in the verb entry narrows down the potential functional description of the subject.
Let us see now how the functional description of the sentence is composed:
According to the rule (5b), the functional description of noun
phrases is built by successively unifying the feature information of
determiners and nouns. Thus, the FDs of NP1 and
NP2 will be, respectively:
|
NP |
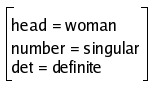 |
|
NP |
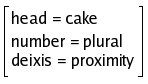 |
Notice that in NP2 the determiner-noun
plural agreement checking is made as a result of unification.
In accordance with the rule (5a) the functional description of the VP
is the result of unifying the FD of the verb made with a
feature object valued with the FD of NP2:
Finally, rule (4) determines that the FD of NP1
is the value of the attribute subject in the FD of the VP.
Note that subject is a complex feature, and that
unification works recursively:
The result is the functional description of the sentence the woman made these cakes.
Typically, unification increases cumulatively the information in the functional descriptions, thus rendering them more and more specific. However, unification may not suppress or alter actual features. This property of unification is called monotonicity.
4.1 Constraint types
The constraint types admitted in GFU-LAB are:
- unification constraints
- negation constraints
- existence constraints
- set membership constraints
Before giving a detailed account of these types, it is pertinent to define the concept of path.
A path consists of a sequence of attributes, which point a value within a FD. Paths always start with a metavariable referring to the FD where they are searched for. Attributes in a path are to be divided by a slash. For instance
U/subject/det
is a path which can be read 'the det of the subject of the mother', and in the FD of (6) has the value 'definite'.
The attribute set of a path may be empty. In this case, the path only consists of a metavariable.
4.1.1 Unification constraints
The general format is
A = B
Where A is a path, whose value unifies with B.
The value B may be an atomic symbol (e.g. in 7a) or
another path (e.g. in 7b and c):
| (7) | a. | D/case = accusative(i.e. the value of the feature 'case' in the associate is the symbol 'accusative') |
| b. | U/object = D(i.e the object of the mother takes the FD of the associate as a value) |
|
| c. | U/subject/number = D/number(i.e the value of the feature number in the submatrix subject
of the mother must unify with the value of the feature 'number' in the
associate) |
A special kind of unification constraint is U=D, which
states that the mother FD unifies with the associate FD.
In addition to pure attributes, paths may also include disjunctions, as shown in:
S --> &NP : U/(subject | object) = D
VP.
This rule (an improved version of 4) states that a sentence (S) consists of an optional NP and a VP. The NP can be the subject or the object of the sentence.
Paths can also refer to a recursive sequence of attributes. Consider the situation where a phrase is separated from its canonical functional position by one or several layers of constituents. This kind of 'long distance' dependency occurs typically between a relative or interrogative pronoun and the clause where the governing verb appears, as in the sentences (8b) and (8c) below (where __ stands for the functional position of the pronoun):
| (8) | (a) | Who __ has arrived? |
| (b) | Who do you think __ has arrived? | |
| (c) | the man that you said that __ had arrived. |
Most long distance dependencies correspond to the phenomenon that Government-Binding Theory handles with move-Α and traces.
The way that GFU-LAB copes with the problem is by using potentially unbounded paths, obtained via recursive attribute sequences, as the one in the example:
U/*a/b = cThis constraint states that c may be value of U/b
(being the sequence *a equal to zero), as well as U/a/b,
U/a/a/b, etc.
Thus, the rule below exemplifies how to use this device in the
treatment of relative clauses (RC) might be the following:
(9) RC --> REL : U/focus=D
S : U=D
U/*scomp/(subject | object) = U/focus.
Where the relative pronoun is a mother feature, called focus.
In its turn, S is augmented with two constraints: the
first (U=D) states that the FD of S has to
unify with the mother FD, and the second constraint claims that the
focus (i.e the relative pronoun REL) may be subject or
object of the relative clause itself, or of some scomp
within.
Paths may also contain evaluators. An evaluator consists of a subpath (enclosed in curly brackets), which must be evaluated before applying the constraint.
Suppose the rule
VP --> VP
PP : U/{D/role}=D.
The constraint attached to the Prepositional Phrase (PP)
says that the FD of a PP will be the value of an
attribute equal to the value of the feature role in the PP.
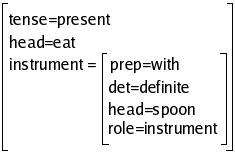
Suppose (10a) is the FD pf the PP with the spoon, and (10b) the FD of eats:
| (10) | a. |  |
| a. | 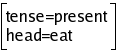 |
The evaluation of {D/role} in (10a) yields instrument,
in such a way that the constraint attached to PP would be interpreted
as U/instrument=D, and would produce:
The system also has a inbuilt function, called {INDEX},
which increases a number counter, and returns the resulting value. It
is possible to call this function in the right hand side of unification
constraints. By doing so, the path automatically takes the value
returned by the function.
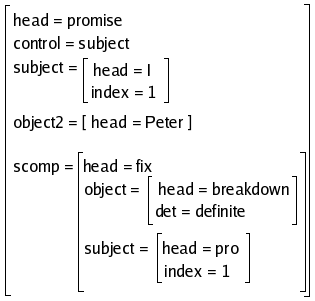
This facility can be used to assign indexes to the referring expressions of an FD, and may be used too (in combination with other constraints) to mark two descriptions as coreferential. Consider the rule
V1 --> V1
VP : D/fverb =c inf
U/{U/control}/index = {INDEX}
D/subject/head=pro
D/subject/index = U/{U/control}/index
U/scomp=D.
This rule applies to Infinitive verb phrases which complement a verb
group (as in I promised Peter to fix the breakdown). Suppose
that via the attribute control, the lexical entries of a
set of verbs are able to express which grammatical function F is the
controller of the subject in infinitive clauses. In promised
the feature at issue will be control=subject, then here F
=subject. Because of the second constraint, we use an evaluator
to assign a numerical index to the FD of F (subject), and then unify
this index with the infinitive clause subject index (the 4th
constraint). The resulting FD will be something like:
4.1.2 Negation constraints
Their form is
NOT A = BWhere A is a path and B its value. This
kind of constraint states that a path A has not the value
B. For instance, (11) asserts that the associate has not
accusative case.
(11) NOT D/case = accusative
If B is the anonymous variable (represenetd as a
question mark), the FD is compelled to assign no value to a given path.
For instance, rule (12) stipulates that a verb next to the particle
'to' is not tensed:
(12) VP1 --> &to
VP / NOT D/tense = ?.
4.1.3 Existence Constraints
Their format is
A =c B
Where A is a path, and B is an atomic
symbol. This kind of constraint is used to check if a particular path A
has the value B instanced. The difference with the
unification constraints will be clear in the example. Let be the FD
(13):
| (13) | 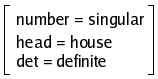 |
The application of the constraint U/count=+ on (13)
yields, via unification, the new FD (14), since the constraint is
compatible with the feature information already present in the FD:
| (14) | 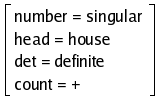 |
If the feature is not present in the FD, unification adds it. In
return, the application of the constraint D/count =c + on
(13) will fail, since the FD does not include a feature count.
4.1.4 Set membership constraints
Feature matrices may include only a feature of every attribute.
Even so, it is sometimes desirable to have more than a member of the
same feature. Suppose, for instance, a feature adjunct,
covering a sort of non-governed complements in a NP (adjectives,
possessives, relative clauses, etc). An utterance like the black
car that John had parked in the street would need two instances of
this feature: one for black and another for that John had
parked in the street.
To render this kind of representation possible, we assume that the
value of the feature adjunct is an open set of FDs.
In order to attach a DF to a set, a special constraint is needed, whose format is:
X1 in X2Being X1 and X2 paths.
Let's see an instance of its use:
NP --> &DET
N
&ADJ : D in U/adjunct
&RC : D in U/adjunct.
Notice that the FD of adjectives and relative clauses is treated as
a member of the set which is value of the feature adjunct
in the NP.
When a single-valued feature is unified with a set-valued one, the single feature is recursively unified against all the feature structures that are members of the set-feature.
For instance, if restrictor labels a set-feature, the
constraint
U/index = U/restrictor/arg1/index.unifies the index value of the mother with the index
value in all the members of the set-feature restrictor.
4.2 Constraint correlations
It is possible to combine constraints in:
- sequences
- disjunctions
- conditional structures
Sequences are formed by chaining constraints, separated by blanks:
VP --> VP
NP : D/type =c time_unit
U/temp=D.
(this rule exemplifies the treatment of adverbial NPs, like those in I wash my car every morning, he came last year, etc)
Disjunctions are put in parentheses, and separated by a vertical bar. For instance:
N1 --> N1
PP : ( U/complement=D |
D in U/adjunct).
This rule states that a PP may be or noun complement or an adjunct.
We can also arrange the constraints in conditional structures of the classical kind:
IF Condition THEN ActionsIF Condition THEN Actions1
ELSE Actions2where Actions1 apply if Condition
succeeds; else Actions2 are tried. Even if Condition
fails, the whole constraint does not.
Both conditions and actions are constraints. An example of this use can be the following rule:
VP --> V
NP : U/object = D
IF D/quantifier =c neg
THEN U/pol = neg.
In English, a negative object (via a negative quantifier) determines
the negative polarity of the whole sentence. So, in a sentence like I
have no book no explicit sentence negator appears. If we want the
sentence FD to be marked as negative, it seems necessary to assign the
feature pol=neg as a result of negative quantification in
the NP.
5. Lexicon organization
5.1 Lexical entries
The main task of the lexicon is to provide the necessary information for building the functional description of linguistic utterances. This information adopts the typical form of sequences of constraints.
Given that GFU-LAB has been thought for syntactic processing, it has no morphological component for the time being. So, the dictionary has to enumerate all word forms, including plural nouns, inflected verbs, and so on.
Lexical entries admit the following formats:
| (15) | a. | Wordform. |
| b. | Wordform = Category. |
|
| c. | Wordform = Category : Constraints. |
|
| d. | Wordform = Category (Class) : Constraints. |
The word form may be composed of any ASCII characters (both basic and extended). Thus, the following forms are admitted in GFU-LAB:
ca˝a cafÚ hń▀lich plašaThose languages which do not employ the Latin alphabet must be transcribed.
The format (15a) is valid for those words that appear as such in the right hand side of a PS rule. For instance, given the rule (16), for the treatment of infinitives
(16) VP --> &to
V1 : NOT D/tense=?.
The dictionary should contain the lexical entry
to.The format (15b) assigns a category to a word. For instance (17)
defines of as a preposition:
(17) of = P.
The format (15c) does not only assign a category to a word form, but also associates a set of constraints with it. These constraints convey the lexical information of the word form.
Las lexical entries with a conceptual referent must contain a value
for the feature head. A head needs to specify the
complements it governs. This is represented as a special feature subcat,
enumerating a set of functions between angle brackets:
paint = V : U/head = paint
U/subcat=.
(This entry states that the verb paint governs a subject and a object).
There are two ways to mark a complement as optional: The one is to
have the complement prefixed with an ampersand (&):
eat = V : U/head=eat
U/subcat=
The other involves to use the inbuilt feature status=opt
in the definition of the complement:
eat = V : U/head=eat
U/subcat=
U/object/status=opt.
The second strategy is convenient when the lexicon is hierarchically
organized (v. 5.2). Suppose that a class of transitive verbs is
defined, with a feature subcat=<subject object>.
Thus, the lexical entry of the transitive verb eat only should
specify that its object is optional.
The declaration of governed functions in subcat serves
other purpose in the system: it forces final representations to be
complete (it is so if all the required complements are instantiated
with a head, otherwise, the representation is rejected as ill-formed).
Besides this information about complement government, lexical entries may collect more prototypical information about the complements. For instance, in Basque, the auxiliaries agree in number and person with the subject, as usual in many languages, but also with the object and the second object. In GFU-LAB it is quite easy to state this information via constraints. For instance:
zaizkit = AUX : U/tense=present
U/object/person=3
U/object/number=plural
U/object2/person=1
U/object2/number=singular
(This entry says that the auxiliary zaizkit requires a third-person plural object and a first- person singular second object.)
Lexical entries may also contain negation and existence constraints. For instance, in German the word form Vater (=father) corresponds to the cases nominative, accusative and dative, what is the same to say that its case is any but genitive. This could be expressed as
(18) vater = N : U/head=father
U/gender=masculine
U/number=singular
NOT U/case=genitive.
Suppose now that a feature loc=+ characterizes the FD
of the PPs introduced by locative prepositions, such as in, on,
between, against, and so on. This feature may be absent
in the other PPs. Thus, in order to describe that the complement of a
verb like put requires a locative PP, an existence constraint
could prove useful:
put = V : U/head=put
U/subcat=
U/complement/locative =c +.
However, neither disjunctions nor conditional statements are admitted in the constraints of lexical entries. In order to have alternatives in the lexicon, the only possibility is to write so many entries as readings we want. The preposition with is a convenient example:
a. with = P : U/prep=with U/type=human U/rol=associative.
b. with = P : U/prep=with U/type=physical_object U/rol=instrument.
c. with = P : U/prep=with U/type=abstract U/rol=manner.
These lexical entries determine the semantic role of the preposition as a function of the semantic type of the phrase.
5.2 Lexical classes and feature inheritance
It is useful to equip the lexicon with the ability of making generalizations concerning lexical classes. For instance, typical objects of German verbs have accusative case, and subjects bear nominative case.
Nevertheless, such generalizations are not exceptionless. For instance, some German verbs have genitive or dative objects.
This kind of facts has induced to apply, in the lexical domain, the techniques of knowledge inheritance and default, primarily used in Artificial Intelligence for Knowledge Representation.
In GFU-LAB, it is possible to declare such lexical classes. These classes must contain constraints stating the information shared by a unitary group of words. Ii is also possible to link a class with a more general superclass.
Classes are declared in the following way:
CLASS Label [ ( Superclass ) ] : Constraints
For instance, we could state our generalization on German verbs above in the following way:
CLASS VT (V) : U/subcat=
U/object/case=accusative
U/transitive=+ .
Equally, we might also define the class V (verb) as:
CLASS V : U/subj/case=nom.
So, particular verbs which belong to these classes will be able to inherit that information. Thus, it is needless to list those features individually for each verb.
In short, in GFU-LAB lexicon can be seen as a hierarchy of classes linked together by inheritance relationships.
The format (15d) enables us to adscribe a word to a particular lexical class. So, the lexical entry of a verb form as erzieht would simply be:
erzieht = V (VT) : U/head=educate
U/tns=present
U/subject/number=singular
U/subject/person=3.
By means of the class VT, erzieht inherits the
subcategorization frame and the features U/object/case=accusative
and U/transitive=+; and because VT is a
subclass of V, it also inherits the feature
U/subject/case=nominative. So, the FD of erzieht would be
finally:
The inheritance of a particular feature from a class does not occur when the lower element has already a specific value for this feature. For instance, consider the word hilft. Its lexical entry could be:
hilft = V (VT) : U/head=help
U/subject/number=singular
U/subject/person=3
U/object/case=dative.
The object case feature is not inherited from the class VT, because the entry is more specific in this respect.
Notice that lexical classes also deal with default features (cf. Bouma 1990).
As far as inheritance is concerned, the subcat feature
should be handled very carefully. As a practical guide, for each
lexical entry, only one subcat feature should be declared
in the hierarchy. The reason for this exception lays in the way the
compiler handles this particular feature. Once the compiler finds a subcat
feature, it creates open features for the subcategorized functions, and
negative features for the ungoverned ones. So, if some other subcat
feature were found upwards in the hierarchy, a feature crash would
certainly arise, leading to a unification failure.
Lexical entries may do reference to the classes they belong to (according to the format 17d). In entries without an overt lexical class, it is assumed that their class is equal to their lexical category (provided it is defined in advance). For instance (19a) is equivalent to (19b):
(19) a. car = N : U/head=car.
b. car = N (N) : U/head=car.
In such a way that (19a) will inherit all the features in the class N.
5.3 Contractions and collocations
GFU-LAB enables to define contractions and collocations composed by sequences of word forms. The former are written as
Contraction -> Wordform* . As in:
a. wanna -> want to.
b. im -> in dem. (in German)
c. du -> de le (in French)
Collocations are introduced as
Collocation <- Wordform* .as in
inspiteof <- in spite of.Collocations must have their own lexical entry in the dictionary.
6. Other GFU-LAB facilities
6.1 Declaration of subcategorized relations
Every grammatical description in GFU-LAB must include a declaration
of which syntactic functions are governed by heads. (There includes all
and every grammatical relation specified within the subcat
features of particular lexical items.) The format of this declaration
is:
FG = Function*A punctual example is:
FG = head subj obj iobj comp xcomp bycomp.6.2 Default statements for Phrases
In GFU-LAB it is possible to state a set of constraints which apply only when a phrase of certain category has been completed. These constraints can be seen as defaults statements for that category.
The format of these statements is:
Phrase ==> ConstraintsConsider some examples:
S ==> U/polarity=affirmative.This statement states that sentences will be marked as affirmative,
hen no other value for the feature polarity is present in
the FD.
S ==> U/subject/head = pro.This rule defines a default pronominal subject (for 'pro-drop' languages).
6.3 Templates
Templates consist of a label which groups together a set of constraint which typically are recurrent in a grammar or lexicon. They observe the following format:
@Label = Constraints.For instance:
(20) @msg = U/gender=masculine
U/number=singular.
Templates may be used in exactly the same contexts where constraints appear: in PS rules, in lexical entries, in default statements and in classes. It is also possible to have templates in the definition of other templates.
For instance, suppose the template (20); we can insert it in the body of the German entry (18), instead of explicitly stating gender and number. The alternative entry would look like
vater = N : U/head=father
@msg
NOT U/case=genitive.
And more importantly, the template may be used in exactly the same way in all the masculine singular nouns in a dictionary of German.
6.4 Hierarchies
Unification does not seem to work properly for certain particular features. For instance, assume the paths
(21) a. U/type=human
b. U/type=institution.
(21a) may be a constraint associated to the subject of a verb as think.
The path (21b) may be typical of words like government or corporation
which refer to human organizations. Hence, one should expect these
paths to unify, since they refer both to human individuals. However,
unification treats human and institution as
different symbols, and fails.
To cope with this problem, GFU-LAB allows to organize the values of some features in a hierarchical scale, so that some of them be supertypes of others. The utility of hierarchical features lies in the fact that supertypes unify with their subtypes, in spite of having apparently dissimilar values.
GFU-LAB facilitates to declare hierarchies of such values, by way of the notation
Supertype < Subtype1 ...
Suptypen.The root of every hierarchy must be named top.
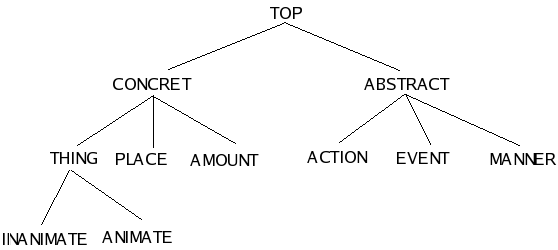
Where hierarchies are more useful is when declaring ontological
types. For instance, following Jackendoff (1983) we may classify the
world concepts in things, places, amounts, actions, events and manners.
Furthermore, we could group the three ones under the supertype concrete
and the rest under the supertype abstract. In its turn,
the type thing might be partitioned in inanimate
and animate, and so on. Similar subclassifications are
possible for the other types.
This ontological hierarchy of should be introduced in the grammar as:
top < concret abstract.
concret < thing place amount.
abstract < action event manner.
thing < inanimate animate.
Assume that hierarchy arrays the values of the attribute ont
(ontology). In such a case, the path U/ont=animate may
unify with U/ont=concret (as they have a common
supertype), but not, for instance, with U/ont=manner.
7. An overview of the parser
When a grammar is loaded, GFU-LAB compiles its content onto PROLOG clauses, appropriate for use with a bottom up parsing algorithm, authored by Y. Matsumoto and his colleagues at ICOT in Japan. Their Bottom Up Parser (BUP) has been designed with the idea in mind to overcome the well-known disability of PROLOG to handle left recursive rules.
In BUP rules are stated as relations between the first constituent of a rule and the other constituents and the mother. To compare a BUP rule with the usual PS rules, consider the following equivalence:
| i. | PS Rule : |
S --> NP, |
| ii. | BUP Rule : |
NP => goal(VP), |
The first rule may be worded as, "in order to find out a sentence (S), it is necessary to look for an NP followed by a VP", whereas the second should read, "if an NP is found, we except to have it followed by a VP, and, being this the case, the whole phrase will be a sentence".
The strategy of BUP tries to avoid useless or redundant computation as much as possible.
One way to achieve this task is top-down filtering. That is done with a table of links between every phrase category and the other categories than may (according to the rules of the grammar) start that phrase.
Furthermore, to cut down the repeated calculations that PROLOG backtracking imposes, BUP uses well-formed constituent and failed constituent tables.
At the same time that the parse tree is been found, the resolution of the constraints attached to each node produces incrementally specified FDs. If constraints fail, the BUP rule at issue is immediately given up, and another alternative is tried. Thus, many search paths are abandoned soon, rendering the parsing process more efficient.
Author: Juan C. Ruiz Anton (ruiz@trad.uji.es)
(Universitat Jaume I, Castellˇ, Spain)
23-January-2004