Calculadora de simetria de modes normals:
Tria un grup de simetria en el desplegable que hi ha més avall. Segons les opcions del teu navegador s'obrirà, es desarà o et preguntarà si vols obrir un fitxer Excel.
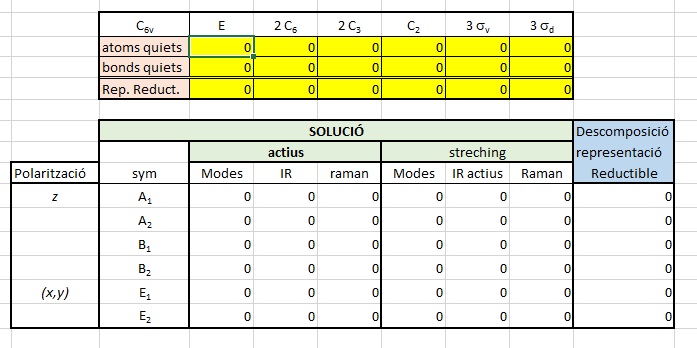
Per exemple, si tries el grup c6v i obres el fitxer excel tindràs aquesta imatge:
Tan sols has d'escriure en les caselles en color groc.
En la primera fila indiques el nombre d'àtoms que no canvien de posició en aplicar l'operació de simetria que té en la casella superior.
En la segon fila indiques el nombre d'enllaços que no canvien de posició en aplicar l'operació de simetria.
A sota hi ha l'output que diu quan modes hi ha de cada simetria, quins són actius en IR i quins en Raman. A la dreta quins entre aquests modes són d'estirament d'enllaç (stretching) i quins són actius en IR i Raman
La tercera fila de color groc és per si vols descompondre la representació reductible que introdueixes en aquesta tercera fila com una suma d'irreductibles. El resultat de la descomposició apareix en la última columna d'output.
Tria el nom del grup de simetria ací:
Una breu fonamentació del procediment
El conjunt de les coordenades moleculars formen base d'una representació reductible del grup puntual de simetria molecular. Les matrius que representen les transformacions en aquesta base tan sols tenen termes no nuls en la diagonal en el cas que la coordenada es transforme en ella mateix (amb una possible fase ±1, cas de representacions reals).
Les coordenades del vector de posició formen bases de representacions irreductibles. La suma dels caràcters de les representacions de les que en formen base és el caràcter de la representació reductible (o irreductible en el cas de grups cúbics --grups del tetraedre, octaedre i icosaedre) del vector de posició. Si multipliquem el nombre d'àtoms que no veuen alterada la seua posició sota l'acció d'una transformació pel caràcter de la representació del vector de posició corresponent a aquesta mateixa transformació obtenim precisament el caràcter d'aquesta transformació quan és representada sobre el conjunt de les coordenades moleculars.
Per tant, per calcular aquest caràcter hi ha prou multiplicar el nombre d'àtoms que romanen quiets sota la transformació pel caràcter del vector de posició (en realitat hi ha prou en considerar una transformació per classe, atès que totes les transformacions d'una classe donen el mateix resultat).
Per determinar el caràcter dels modes normals cal restar-hi translacions i rotacions. Acudim a la taula de caràcters i sumem les irreps que tenen de base les components del vector de posició(x,y,z) i de les rotacions (Rx,Ry,Rz) --en cas de molècules lineals no hi ha rotació sobre l'eix molecular z i per tant cal NO restar Rz-- Escrivim el caràcters dels modes normals com un vector columna P.
Si multipliquem cada fila Mi de la taula de caràcters M per la multiplicitat xi que apareix en la descomposició de P com suma de representacions irreductibles, obtenim P com vector fila. Per tant, anomenant Mt a la trasposta de M i X al vector columna de les multiplicitats tenim què: Mt·X = P. I si anomenem (Mt)-1 a la matriu inversa d' Mt podem aïllar la X: X = (Mt)-1 ·P
Cas de grups amb representacions E complexes (per exemple el grup C3h en que la representació E en realitat en són dues complex conjugades), per poder treballar amb nombres reals fem la suma de les dues representacions conjugades. El problema és que la taula de caràcters deixa de ser una matriu quadrada i per tant no podem calcular l'inversa de la seua trasposta. Aleshores calculem la inversa del producte M·Mt:
Mt·X = P → M· Mt·X = M·P → X = (M·Mt)-1 ·M·P.