En absència de forces externes les partícules segueixen trajectòries rectes a l'espai - temps Euclidià. La recta és la distància més curta entre dos punts d'aquest espai. En un espai corbat, com ara la superfície d'una esfera, la trajectòria de recorregut mínim és anomenada geodèsica.

Afirmem que les partícules segueixen SEMPRE trajectòries geodèsiques. La presència d'una massa origina una força gravitatòria perquè deforma l'espai - temps. La força no és més que aquesta deformació que fa que la recta deixe de ser geodèsica.

Per exemple, si hi ha una força F = mg, aleshores la relació entre l'espai x i el temps t ve donada per x = 1/2 g t² , expressió que representa una paràbola en (x,t), on la geodèsica és la recta.

Si afirmem que la gravetat el que fa és dilatar/contraure l'espai (fer-lo curvilini) convertint x en x' de manera que (x')² = x, aleshores,

que representa una recta en (x',t). La dilatació/contracció de d'espai es apercebuda com acceleració/desacceleració. Així quan l'espai es dilata no apreciem la dilatació, veiem que la partícula corre menys, que es desaccelera, i descrivim aquesta desacceleració com l'acció d'una força sobre una partícula que es mou en un espai Euclidià, o alternativament diem que la partícula es mou lliure a través d'un espai corbat.

Podem pensar que allò que apreciem com x' és una espècie de projecció de les coordenades x sobre un espai Euclidià. Les coordenades x conformen un espai enrotllat, de manera que les trajectòries amb velocitat constant sobre x es veuen amb velocitat variable sobre x'.

És, doncs, el temps simplement la quarta dimensió de l'espai? La primera cosa que observem és que espai i temps tenen distintes unitats i per a poder comparar dues magnituds cal prèviament escriure-les en idèntiques unitats (no comparem mai una distancia en cm amb un altra en Km). Anomenem c al factor de conversió que permet que (ct) presente les unitats adients per a ser comparat amb x..

Quant val c? El concepte de simultaneïtat ens donarà la resposta. Simultaneïtat que significa distància zero en l'espai - temps de l'observador. Imaginem dos events simultanis en dos punts: el punt A, on està situat l'observador, i el punt B, a una distància x de l'observador, on s'encen una llum. L'observador veu la llum simultàniament a un event en A (d = 0) si aquesta, la llum, fou encesa un temps t= x/c abans (c és la velocitat de la llum).

La distància entre dos punts en l'espai Euclidià és d²=x²+y²+z². Podríem pensar que la distància en l'espai - temps queda definida, per analogia, (considerarem per simplicitat una única dimensió espacial x):

Si considerem però el cas anterior de dos events simultanis, on x = ct, ens adonem de seguida que cal redefinr la distancia en la forma:

d²=x²-(ct)²,

atès que volem que aquesta definició siga coherent amb el concepte de simultaneïtat. (Podríem mantenir la mateixa expressió si en lloc de (ct) escrivim (ict), on i²= - 1).

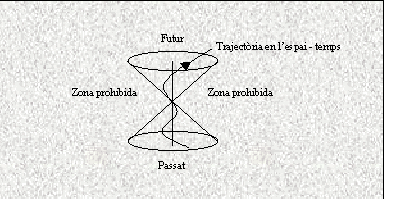
Els successos simultanis són aquells que d²=x²-(ct)²=0 => x²=(ct)². Si representem aquesta igualtat en (x, ct) generem una superfície cònica.

Si d²>0 => x²>(ct)² => mai podríem detectar aquest succés (no aplegarà mai la llum a l'observador).Aquesta desigualtat representa els punts exteriors a la superfície cònica que anomenarem zona prohibida

Si d²<0 => x²<(ct)² i parlem de successos detectables. Aquesta desigualtat representa els punts interiors a la superfície cònica.

Una trajectòria en l'espai - temps mai pot retrocedir en el temps (però si en l'espai) perquè hauria de passar necessàriament per la zona prohibida. La nostra experiència està, doncs, d'acord amb les fórmules.